圆孔夫琅禾费衍射图样的三维特性分析

于建强 谢 亮 铁小匀 安艳伟 张进治

(北方工业大学理学院，北京 100144)

光的衍射是基本物理现象之一，深入研究衍射图样的光强分布对光学成像和光学设计等有着重要的意义。光学仪器的光瞳大都是圆孔形状的，光学成像系统大都是平行光入射的，因此研究圆孔夫琅禾费衍射对光学仪器的分析有重要的作用[1]。衍射图样一般使用菲涅耳-基尔霍夫衍射积分公式推导获得，大学物理教材中一般仅使用贝塞尔函数描述几何焦平面上的二维衍射图样，而对于离焦点的光强分布由于需要更复杂的特殊函数，一般不予介绍，限制了对衍射图样的深入理解[2]。

本文基于菲涅耳-基尔霍夫衍射积分公式，推导了圆孔夫琅禾费衍射图样的一般表达式，并使用Matlab软件的integral2二重积分函数进行了数值积分，获得了衍射图样的三维光强分布，给出并分析了衍射焦斑的横向和轴向光强分布图，加深了对圆孔夫琅禾费衍射的理解。

1 理论推导

一束单色平面光经圆孔衍射，通过理想透镜后形成一个会聚的球面波，根据几何光学理论此球面波应汇聚在几何焦点O，但因光的衍射，焦点附近的P点亦有光波到达。以O点为坐标原点，光轴方向为z轴，x轴、y轴在与z轴垂直的平面内，建立如图1所示的右手直角坐标系。

图1 圆孔夫琅禾费衍射示意图

真空中波长为λ的入射光，在波阵面上的复振幅为E0(Q)，P点与波阵面上某点Q的距离为r，根据菲涅耳-基尔霍夫衍射积分公式和基尔霍夫边界条件，P点的总振动可由Q点dΣ面元的振动遍历整个开孔区域Σ0积分获得[3,4]：

(1)

其中,k=2π/λ为波数;θ0和θ为波振面的法线与入射光方向和场点P方向的夹角，在远场傍轴条件下θ0≈0,θ≈0，透镜半径a≫λ，透镜焦距f≫a，r≈f，且E0(Q)与位置基本无关，即E0(Q)=E0，将上述近似代入式(1)可得：

(2)

(3)

积分面元为dΣ=ρ′dρ′dφ′，将式(3)代入式(2)，并将与积分变量无关项移至积分号前，则焦点附近的三维振幅分布为

(4)

数值计算式(4)即可得到焦点附近的振幅分布，根据光强定义式可得光强的三维空间分布为

(5)

其中,c为真空中光速;n为折射率;ε0为真空中介电常数

2 衍射图样的三维光强分布

使用Matlab软件的二重积分函数integral2数值计算了式(4)、式(5)，数值计算参数如下，衍射圆孔半径a=2.8mm，透镜焦距f=8.4mm，光速c=299792458m/s，真空介电常数ε0=8.85×10-12F/m，入射光真空波长λ=500nm，入射光功率P0=1mW。

2.1 几何焦平面上的光强分布

几何焦平面上，z=0，式(4)化简为

(6)

与教材中给出的结果一致[1]，圆孔夫琅禾费衍射图样在焦平面上的分布具有圆对称性，如图2所示，其中图2(a)为横向分布伪彩图；图2(b)径向强度分布图，可以看出衍射图样在几何焦点处为一亮斑，称为艾里斑，周围是以几何焦点为对称中心，明暗相间的同心圆环，亮环的强度随着半径的增大而急剧下降。为了更加直观地观察衍射图样的分布特征，对图2(a)和图2(b)中的光强取以10为底的对数作图，分别如图2(c)和图2(d)所示，可以看出随着径向距离的增大，相邻暗环的间隔趋于相等。

图2 几何焦平面上的光强分布图

2.2 轴向光强分布

轴向光强分布如图3所示，其中图3(a)、(b)为光强轴向伪彩图和轴向强度分布图，可以看出艾里斑呈现管状结构，且轴向尺寸大于横向尺寸。为了更加直观地观察衍射图样的周期性，对图3(a)、(b)中的光强取以10为底的对数，如图3(c)、(d)所示，其中图3(c)中的虚线为几何光束边界。从图中可以看出衍射图样在焦平面前后是对称的。

表2给出了光轴上光强分布的前7个极值，可以看出光轴上的光强分布也具有周期性，并且暗点的间隔相等。

表1 焦平面上径向光强分布的前7个极值

图3 轴向光强分布图

表2 光轴上光强分布的前7个极值

2.3 离焦图样

图4展示了衍射图样的离焦性质，其中图4(a)～(h)依次为z=0, 18λ, 25.75λ, 36λ, 44.26λ, 54λ, 62.48λ, 72λ处的光强横向分布图，图中的光强皆做了以10为底的对数处理。可以看出随着z的增加，光的能量径向向外弥散。

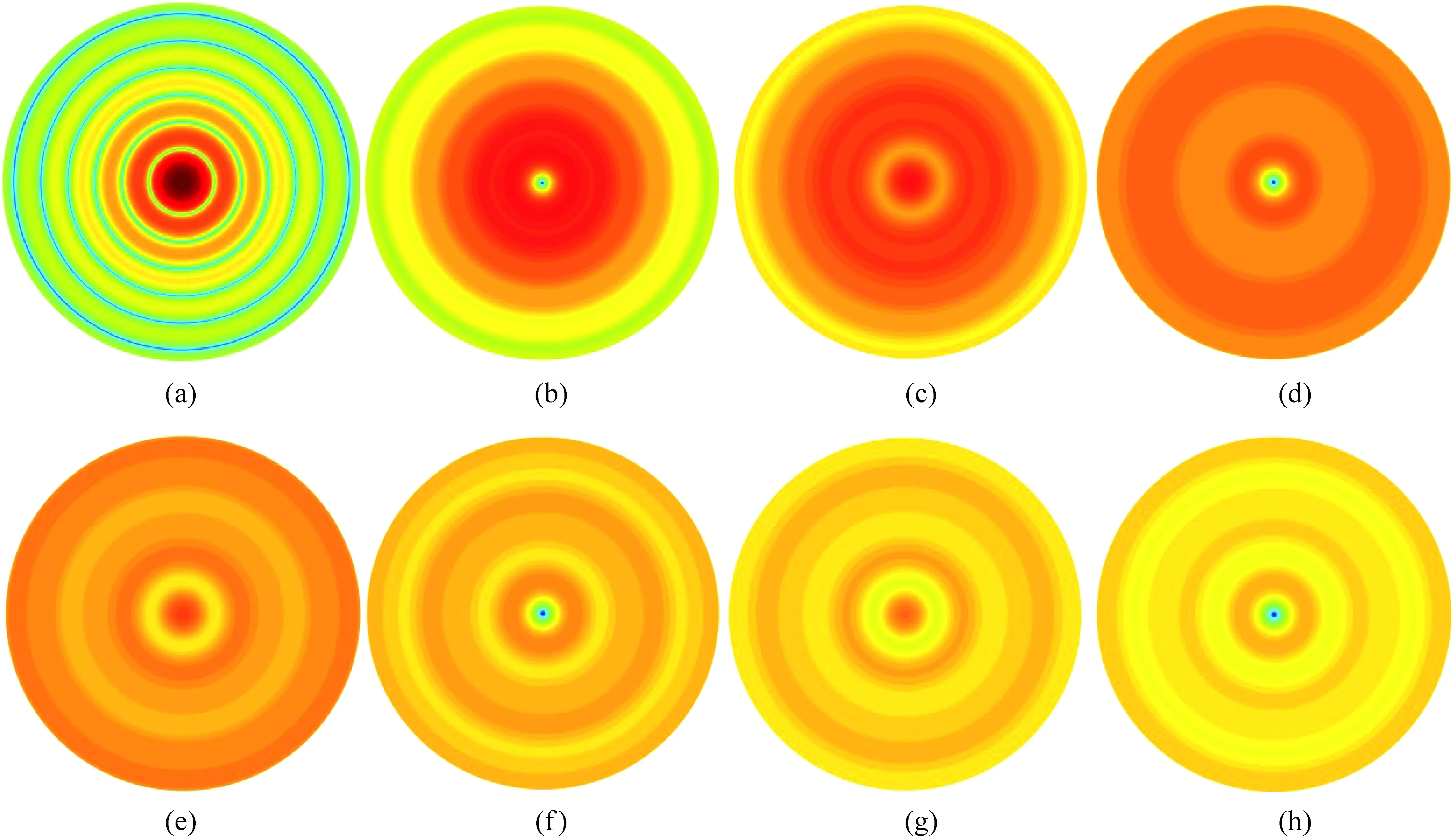
图4 离焦的横向光强分布

3 结语

本文基于菲涅耳-基尔霍夫衍射积分公式，推导了圆孔夫琅禾费衍射的积分表达式，使用Matlab软件数值计算了艾里斑的三维光强分布，分析了圆孔夫琅禾费衍射图像的三维光强衍射图样，加深了对圆孔夫琅禾费衍射的理解。