一个绳杆复合摆问题的简单研究

朱经亚

(武汉大学物理科学与技术学院，湖北 武汉 430072)

轻绳、均质刚体杆、单摆、复摆是中学物理和大学普通物理中非常常见的模型，对于参加全国中学生物理奥林匹克竞赛复赛和决赛的同学更是司空见惯。近年来竞赛题目多由大学教师命题，题目多与大学教师科研题目相结合，模型呈现出复杂化的趋势。2016年决赛[1]的题目2比较另类，直接把常见的单摆中质点改为匀质刚体杆，模型可谓非常简单，并且在现实生活中用一条绳子和一根筷子就可做简单的实验。该问题对于培养学生勤于思考的习惯、灵活运用物理知识解决问题的能力具有重要意义。下文第1部分我们首先引用和描述该题目；然后第2部分简单阐述该题目的多种解题方法，并用守恒定律、牛顿定律的方法简要给出结果；第3部分对绳和杆近似共线的情况做重点分析，并给出数值模拟结果；第4部分小结。

1 题目描述[1]

如图1(a)，AB为一根匀质细杆，质量为m，长度为l2；杆上端B通过一不可伸长的软轻绳悬挂到固定点O，绳长为l1。开始时绳和杆均静止下垂。此后所有运动均在同一竖直面内进行。

图1 题目原图[1]，包括图1(a)和图1(b)

(1) 现对杆上的D点沿水平方向施加一瞬时冲量I，若在施加冲量后的瞬间，B点绕悬点O转动的角速度和杆绕其质心转动的角速度相同，求D点到B点的距离x和B点绕悬点O转动的初始角速度ω0。

(2) 设在某时刻，绳和杆与竖直方向的夹角分别为θ1和θ2(如图1(b)所示)，绳绕固定点O和杆绕其质心转动的角速度分别为ω1和ω2，求绳绕固定点O和杆绕其质心转动的角加速度α1和α2。

2 解题方法和结果简述

题目第一问较为简单，这里直接给出结果

下面主要看第二问。解决一个经典力学问题，一般可以采用牛顿定律或转动定理、三大守恒定律或定理、拉格朗日力学、哈密顿力学、哈密顿原理等多种方法[2]，下面我们就对用这些方法解决该问题做简要的阐述。

(1) 牛顿定律和转动定理方法

参考系选择可以采用惯性参考系，也可以采用非惯性参考系。对于惯性参考系，可以采用水平竖直方向的坐标系，也可以采用沿杆方向的坐标系，或者沿绳方向的坐标系。其中沿绳方向的坐标系相对较为简便，首先进行受力分析，由牛顿定律、转动定理列出3个方程，然后由其中两个方程解得绳中的张力T和杆的角加速度α2，再代入第三个方程解得绳的角加速度α1。对于非惯性参考系，以B点为坐标原点，建立随B点运动的动坐标系，引入惯性力来解决问题。

(2) 机械能守恒定律和角动量定理方法

该系统没有摩擦，所以机械能守恒。由于只有杆有质量，故机械能应包括杆的平动动能、转动动能，以及杆和地球之间的重力势能。O点固定，以O点为参考点，绳的张力力矩始终为零，只有重力有冲量矩，可利用角动量定理。因题目要求的是角加速度，所以机械能、角动量都需要对时间求一阶导数，从而可列出两个方程，解得两个角加速度。守恒定律方法不需考虑内力，较之牛顿定律方法简单。

(3) 拉格朗日力学方法

采用拉格朗日力学的一般方法，该系统有两个自由度，可以先选定两个广义坐标，写出系统的拉格朗日函数，然后求一阶和二阶导数，利用拉格朗日方程可列出两个方程，从而求得两个角加速度。拉格朗日力学的一般方法较牛顿定律方法分析过程简单，但数学计算过程比守恒定律方法复杂一些。对于这个问题，因为系统为完整、保守、稳定系统，且拉格朗日函数不显含时间t，所以系统的广义能量，也即系统的机械能为运动积分/守恒量[3,4]；再利用一个拉格朗日方程，即可求出两个角加速度。这个拉格朗日力学的特殊方法最后还是归结到运用守恒定律。

(4) 哈密顿力学方法

按照哈密顿力学的一般方法，可以先选定两个广义坐标，写出系统的拉格朗日函数，进而写出哈密顿函数，哈密顿函数为关于两个广义坐标、两个广义动量的函数。根据哈密顿正则方程，可得到4个一阶微分方程组，从而可解得两个偏转角、两个角速度的表达式，对角速度求一阶导数即可得到角加速度。哈密顿力学方法所需求解方程个数比拉格朗日方法多一倍，一般情况下更为复杂。

(5) 哈密顿原理

哈密顿原理是经典力学最基本原理之一，在保守系统中可由哈密顿原理推导出拉格朗日方程、哈密顿正则方程、牛顿第二定律，所以原则上也可从哈密顿原理出发来解决这个问题。但实际上，从哈密顿原理出发最终还要归结到以上几种方法。

通过对以上多种方法的分析，可看到，最简便直接的方法是机械能守恒定律和角动量定理方法，下面简要给出这个守恒定律方法的过程。

杆的总角动量为

(3)

由角动量定理

(4)

杆的总机械能为

(5)

由机械能守恒知

(6)

由式(3)～式(6)得到

联立式(7)、式(8)可解得

(9)

与守恒定律方法相比，牛顿定律方法需要考虑内力，过程较为繁琐，且方向等问题较易出错，在此我们也简单列出在惯性参考系沿绳坐标系中用牛顿定律的方法作为对比。在O、B、A3点所在的竖直平面内，以O为原点、沿绳斜向上的射线为y轴、垂直于绳斜向右的射线为x轴，建立平面坐标系。杆的质心C的加速度(aCx,aCy)满足质心运动定理

(10)

式中，T是绳的张力的大小。同时，杆在绳张力T相对于杆的质心的力矩作用下绕质心转动，由转动定理得

(11)

由绳的几何关系得B点的加速度为

(12)

由杆的几何关系还可得B点的加速度为

(13)

由式(10)～式(13)，消去B、C点的加速度，可得3个方程，联立3个方程即可解得两个角加速度α1和α2和绳中张力T。

3 绳和杆近似共线情况分析

由题目结果式(9)可看出，一般情况下绳和杆的摆动应该是不规则的，这一点也可做简单实验来验证。但是通过不同情形多次测试，会发现在某些条件下绳和杆的摆动会呈现出规律性，比如绳和杆近似共线同步摆动。鉴于此，可再对题目追加一问：定性分析绳和杆在运动中近似共线的条件，并定量求绳和杆近似共线情况下在不太长时间内绳、杆与竖直方向的夹角θ(t)。

对于这一个问题，首先可以想象，假设杆无限短，则系统可近似为单摆；假设绳和杆一直共线，则杆上的每一小段都可看做单摆的摆子。由单摆的运动规律经验，可以判断，绳和杆摆角幅度应该比较小，杆上每一点也即绳和杆的初始角速度应该相等，杆相对于绳应该较短。

若微小瞬时冲量I施加后绳和杆在运动中近似共线，则可考虑做近似处理，视杆和绳严格共线：则二者以相同角度摆动，绳上各点之间、以及与杆上各点之间相对距离不发生改变，即在运动过程中绳与杆构成一个刚体，由此问题得以简化。在该刚体的质心C运动到最高点的过程中，刚体系统的机械能守恒，有

(14)

式中，θm是绳与竖直方向的最大夹角。由题意，初始冲量I微小，则θm应很小，有

(15)

该刚体运动过程中，仅重力对其产生转动力矩M，且绳与竖直方向的夹角θ≤θm，故θ应很小

(16)

由刚体转动定理得

(17)

由式(16)、(17)式得

(18)

式中ω是一个常量

(19)

由式(18)、(19)知，刚体做简谐振动，解为

θ=θmcos(ωt+φ0)

(20)

其振动角频率ω由式(19)确定；由式(14)～式(17)和初始条件得，振幅θm和初相位φ0分别为

(21)

至此，题目得以解决。但是我们判断的绳和杆近似共线的条件是否正确，以及假设绳和杆严格共线的近似结果是否与实际相符，还存在一定疑虑。为了检验以上的判断和近似处理方法，可以采取实验定性检验和理论模拟[5-7]检验。实验所需器材非常简单，一根绳子和一根筷子就可以做定性判断。通过实验，证实了我们判断的正确性。对于理论模拟，我们考虑了表1中所列5种情况，利用公式(9)的两个二阶微分方程，用Mathematica进行数值模拟、绘图，相当于理想的真实运动情况。作为对比，还给出了假设严格共线的近似计算结果，在表1中还利用式(1)、(2)、(19)、(21)给出了冲击点位置、初始角速度、周期、最大摆角。模拟结果展示在图2～图12中，其中黑色曲线为假设绳和杆严格共线的近似结果，为标准的正弦/余弦曲线；灰色曲线反映了绳与近似结果的偏差；虚曲线反映了杆和绳的偏差。

由图2～图4可看出，在10s(约9个周期)内P1情形下绳和杆的摆角、角速度差别较小，并且与假设严格共线情形下得到的结果符合程度很高；角加速度虽然与假设严格共线摆动的近似结果也近似相等，但绳和杆之间可能会有相对较大的差别。这是由于与刚体杆复摆类似，绳、杆的内力及相互作用力约束了绳、杆近似共线，近似做简谐摆动；只是绳的约束效果弱于刚体杆，自由度大一些，所以绳和杆的角加速度可能会有较大的差别。

表1 用Mathematica进行数值模拟所考虑的5种情况，选定x使绳和杆的初始角速度相同，并假设绳杆严格共线计算出初始角速度、最大摆角、摆动周期

图2 P1情形下的绳、杆的摆角变化关系图横轴为时间，长度为10s。其中黑色曲线为假设绳杆严格共线得到的摆角θ(t)，灰色曲线为绳与近似结果的摆角差θ1(t)-θ(t)，虚曲线为杆与绳的摆角差θ2(t)-θ1(t)

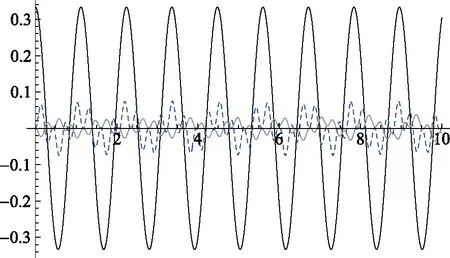
图3 P1情形下的绳、杆的角速度变化关系图横轴为时间，长度为10s。其中黑色曲线为假设绳杆严格共线得到的角速度灰色曲线为绳与近似结果的角速度差曲线为杆与绳的角速度差

图4 P1情形下的绳、杆的角加速度变化关系图横轴为时间，长度为10s。其中黑色曲线为假设绳杆严格共线得到的角加速度灰色曲线为绳与近似结果的角加速度差虚曲线为杆与绳的角加速度差

由图4～图6可以看出，杆相对于绳越短，它们的角加速度差别越小。这是由于杆相对于绳越短，该绳杆复合摆越接近于单摆，绳和杆的角加速度也越接近于单摆的角加速度，所以绳和杆的角加速度越接近。实际上，假设绳、杆严格共线统一描述了单摆和复摆的情况，只是当杆相对于绳较长时所需绳和杆之间的约束力就相对较大一些，由转动定理知它们的角加速度差别也就越大。

图5 P2情形下的绳、杆的角加速度变化关系图横轴为时间，长度为10s。其中黑色曲线为假设绳杆严格共线得到的角加速度灰色曲线为绳与近似结果的角加速度差虚曲线为杆与绳的角加速度差

图6 P3情形下的绳、杆的角加速度变化关系图横轴为时间，长度为10s。其中黑色曲线为假设绳杆严格共线得到的角加速度灰色曲线为绳与近似结果的角加速度差虚曲线为杆与绳的角加速度差

图7 P4情形下的绳、杆的摆角变化关系图横轴为时间，长度为40s。其中黑色曲线为假设绳杆严格共线得到的摆角θ(t)，灰色曲线为绳与近似结果的摆角差θ1(t)-θ(t)，虚曲线为杆与绳的摆角差θ2(t)-θ1(t)

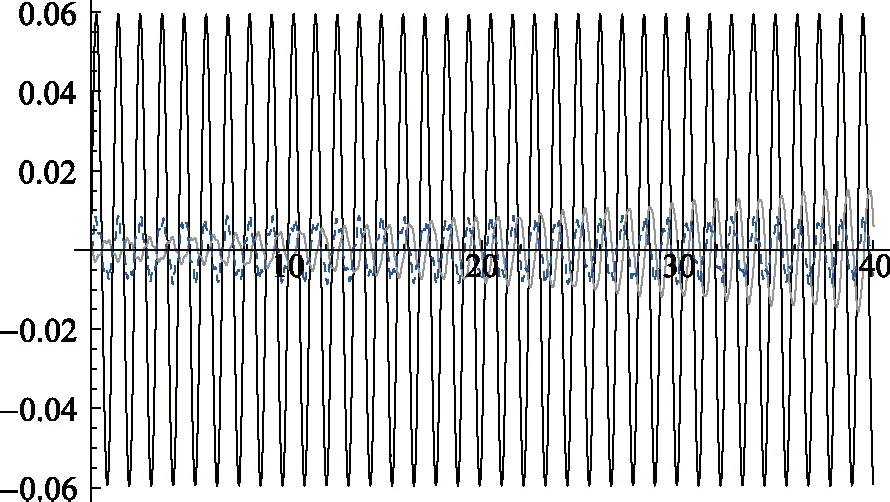
图8 P1情形下的绳、杆的摆角变化关系图横轴为时间，长度为40s。其中黑色曲线为假设绳杆严格共线得到的摆角θ(t)，灰色曲线为绳与近似结果的摆角差θ1(t)-θ(t)，虚曲线为杆与绳的摆角差θ2(t)-θ1(t)

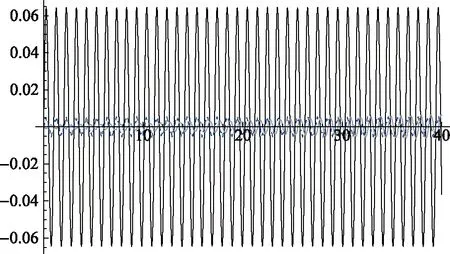
图9 P2情形下的绳、杆的摆角变化关系图横轴为时间，长度为40s。其中黑色曲线为假设绳杆严格共线得到的摆角θ(t)，灰色曲线为绳与近似结果的摆角差θ1(t)-θ(t)，虚曲线为杆与绳的摆角差θ2(t)-θ1(t)

图7～图9反映了较长时间(几十个周期)内绳、杆摆角随时间的变化关系。由此可以看出，较长时间内杆和绳仍能保持近似共线，但假设严格共线得到的摆角变化结果却和实际情况有所偏差。杆相对于绳越短，偏差越不明显。这是由于绳杆复合摆实际自由度为2，假设严格共线我们只考虑了杆绕固定点摆动一个自由度，实际上还有杆在每时刻的共线位形附近做微振动这个自由度。由机械能守恒知杆的微振动不改变最大摆角，但使得摆动平均角速率减慢，所以相对于严格共线情况摆动周期偏大，随着时间的积累将会出现较大偏差。杆相对于绳越长，杆的转动惯量越大，需要考虑的微扰效应也就越大，该微扰效应在改变角加速度和角速度上较明显，摆角上的偏差则在较短时间(几个周期)内相对不太明显。图10～图12为杆长远大于绳长的情况，很好地说明了这个问题。

图10 P5情形下的绳、杆的摆角变化关系图横轴为时间，长度为60s。其中黑色曲线为假设绳杆严格共线得到的摆角θ(t)，灰色曲线为绳与近似结果的摆角差θ1(t)-θ(t)，虚曲线为杆与绳的摆角差θ2(t)-θ1(t)

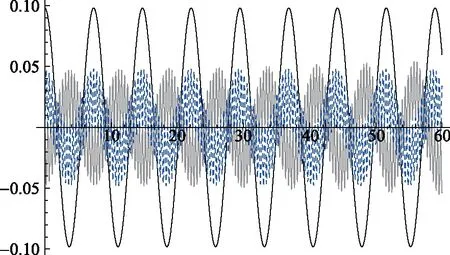
图11 P5情形下的绳、杆的角速度变化关系图横轴为时间，长度为60s。其中黑色曲线为假设绳杆严格共线得到的角速度灰色曲线为绳与近似结果的角速度差曲线为杆与绳的角速度差

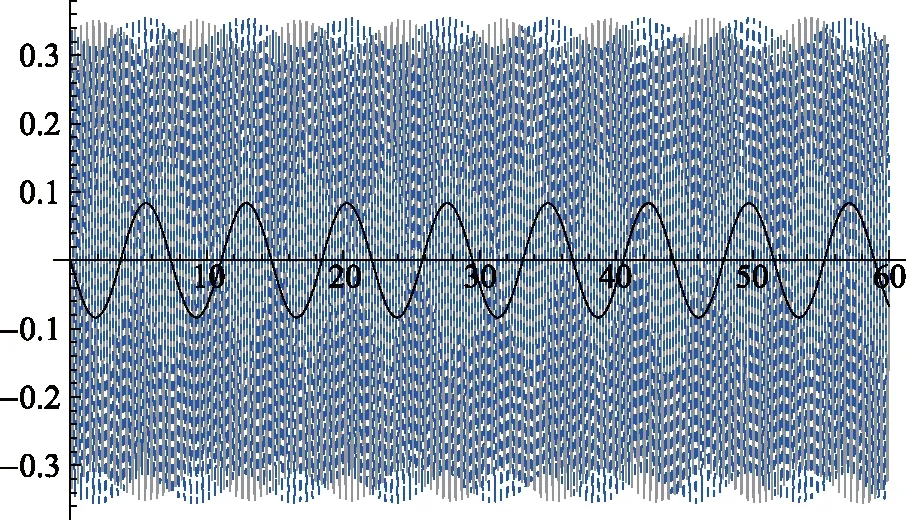
图12 P5情形下的绳、杆的角加速度变化关系图横轴为时间，长度为60s。其中黑色曲线为假设绳杆严格共线得到的角加速度灰色曲线为绳与近似结果的角加速度差虚曲线为杆与绳的角加速度差

4 总结

本文从一道全国中学生物理奥林匹克竞赛题目出发，研究了绳杆复合摆的问题。首先引用题目，然后简要阐述各种解法，包括牛顿定律和转动定理、守恒定律和定理、拉格朗日力学、哈密顿力学、哈密顿原理等。接着对题目进行拓展，重点分析了绳杆近似共线的问题，包括近似共线的依赖条件、假设严格共线的近似处理方法及其与实际情况的偏差等，并对该问题进行了详细的数值模拟，以及通过绘图形象地展示了我们的结论。

通过一系列分析和验证，得出在绳杆复合摆系统中，绳和杆近似共线同步摆动的条件为：

(1) 冲量作用点一定，使得绳和杆初始角速度相同；

(2) 冲量较小，使得偏转角度较小，实际上偏转幅度小于0.5rad时线性都比较明显；

(3) 杆长小于绳长。

满足这3个条件时，绳杆近似共线，并且在短时间内假设绳杆严格共线是一个很好的近似。

值得注意的是，在以上条件下绳和杆的摆角、角速度都近似相等，并且几十个周期内与假设严格共线的近似结果符合较好。角加速度虽然与假设严格共线的近似结果也近似相等，但绳和杆之间可能会有相对较大的差别。特别是对于杆相对于绳较长的情况，角加速度、乃至角速度的偏差会较大。在长时间内，为了更精确地描述绳杆复合摆问题，尤其对于杆相对于绳较长时，应该考虑杆在共线位形附近的微扰。