平面化的引力波及其振幅的估算
宁 专 宋振宁 邢志忠
(中国科学院大学物理科学学院,北京 100049)
爱因斯坦创建于1916年的广义相对论预言了引力波的存在[1],其本质在于时空曲率由于大质量物体的波动而产生周期性的变化,同时造成能量辐射。直到2016年2月11日,美国的LIGO合作组才第一次宣布直接探测到了令人信服的引力波信号,后者是由双黑洞系统从渐进旋近到融为一体的过程中产生的[2]。这一具有里程碑意义的发现正式开启了引力波天文学的大门,随后引力波也成为科学普及工作的重点之一。但时至今日,科普文献中鲜有针对引力波振幅的浅显描述。本文旨在避开利用广义相对论计算引力波源处的振幅的复杂性,直接考虑引力波在空间传播过程中造成的两物体之间距离的周期性增减,从而定义相应的振幅,并利用大学本科一年级的知识估算引力波振幅的大小。

图1 在二维平面上形象化的引力波
引力波在三维空间中自由传播时,自身强度不会发生变化,而波形可以形象化地在二维平面上展示出来,如图1所示。从科普的角度出发,我们提出一个简单的玩具模型:假设引力波在二维空间中传播,其波形可以用诸如正弦曲线等平面曲线来描述。在这种情况下,给定“空间”中两个物体A和B,设它们之间的距离在不受引力波影响时为L,而在引力波经过时距离的最大改变为ΔL(取正号),则引力波的振幅即可定义为h=ΔL/L。
以LIGO实验为例,其观测引力波的基本思路是直接测量引力波经过探测器时所造成的臂长的微小变化。取LIGO探测器的原始臂长为L,实验过程中测得的最大臂长记为L+ΔL,则引力波的振幅即为前面所定义的h=ΔL/L。由于LIGO探测器的距离分辨率精度达到了质子直径的千分之一,即10-18m的量级,而其臂长为4km,因此可以探测振幅处于10-22~10-21水平的引力波信号。
当基于上述玩具模型在二维空间中考察A和B两个物体之间因引力波经过所造成的距离变化时,至少存在两种形象化的理解方式:一种理解是把引力波的效应想象成波浪,A和B两者之间的水平距离为L,但从A到B沿着测地线所走的路程增大,其长度为L+ΔL;另一种理解是将引力波效应想象成绳子,A和B两者之间的绳长L不变,但当它变得弯曲之后,两端的水平距离变小,其长度为L-ΔL。本文拟以第一种方式说明引力波振幅的计算。
首先以正弦曲线函数y=sinx为例做初步的振幅计算演示。取一周期的正弦曲线波形如图2(上)所示,当引力波未经过二维空间时,物体A与B之间的距离为L=2π。引力波造成的两者之间的测地线长度即为正弦曲线的长度为

图2 玩具模型中的正弦曲线(a)与抛物线(b)波形
其中积分可表达成如下形式:
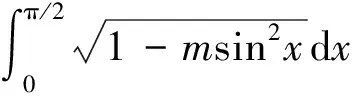
从而该平面正弦引力波的振幅为
其实引力波的振幅极其微小,其数量级大致在10-36~10-20之间。因此当取正弦曲线作为二维引力波的波形时,前者的振幅必须比1小很多。
考虑一般的正弦曲线函数y=asinbx,用同样的方法得到L=2π/b,以及
从而得到振幅
由此可以看出引力波的振幅只与正弦曲线的振幅及其角频率的乘积有关,这意味着由曲线y=a1sinb1x和y=a2sinb2x描述的引力波在a1b1=a2b2时其实具有相同的振幅。在ab≪1的情况下,可以把第二类完全椭圆积分作级数展开到次领头阶,于是上面的振幅表达式简化为
因而当h≈10-36~10-20时,即得到ab≈10-18~10-10的限制。可见引力波造成的时空涟漪,是极其微弱的。
上面的例子由于涉及第二类椭圆积分而无法用常见的基本函数来表达它的精确解析解。下面再举一个解析上严格可解的例子,来说明二维引力波的振幅计算。不妨采用二次函数y=-4ax(x-π)/π2的图像在[0,π]区间的x轴上方部分作为波形的1/2周期代替正弦曲线的1/2周期,如图2(b)所示,则该抛物线在[0,π]区间内的长度就是抛物线y=-4ax2/π2在[-π/2,+π/2]区间内的长度,即
其中b≡4a/π。于是该引力波振幅的严格表达式如下:
当a取值非常小时,上式的解析近似结果为h≈b2/4。因此h≈10-36~10-20意味着b≈10-18~10-10,与前面正弦曲线的例子类似。
最后需要说明的是,虽然引力波在空间的传播依赖于时间,但上述估算引力波振幅的方法只考虑了一周期内波形的变化,因此与时间无关。真实的引力波具有极其复杂的波形,自然不是简单的基本函数所能描述的。尽管如此,我们相信简化了的玩具模型仍然具有一定的科普意义。

