陀螺进动中的“角动量不守恒”问题
邵怀华 卓玉霖
(六盘水师范学院电气工程学院,贵州 六盘水 553000)
在回转效应演示实验中,为了突出进动这一“反抗”重力的神奇力学现象,往往通过给陀螺仪一个较大的自转角动量等方式减小其章动,但是这样会产生竖直方向的进动角动量从何而来的疑问。图1所示为回转效应演示仪简化模型,L为自转角动量,R为回转半径,O为支点。为了讨论方便,假设陀螺质量为m,质心在悬空端P点。

图1 回转效应演示仪简化模型示意图
均匀进动时,由力学基本知识可知
(1)
1 陀螺动力学分析

图2 陀螺转动的矢量分析图(a) 纵向转动; (b) 横向转动
令ωp和ωn分别表示进动和章动角速度的大小。分析图2(a),可得如下方程组
(2)
式中ax表示陀螺在惯性力作用下水平运动加速度的大小。上式可解得关于ωp和ωn的微分方程
(3)
同样,分析图2(b)可得
(4)
解得
(5)
联立式(3)、式(5),结合初始条件ωp(0)=0,ωn(0)=0可得进动和章动角速度大小随时间的变化关系
(6)
进而对两个角速度分别求积分,可以得到进动角θ和章动角α随时间的变化关系,结合初始条件θ(0)=0,α(0)=0可得
(7)

图3 理想情况下陀螺仪悬空端P的空间轨迹
此即理想情况下,关于回转仪悬空端P运动行为的一个较为精确的解。图3是对理想情况下回转仪悬空端P轨迹的数值模拟结果。可以看出水平释放后陀螺并不是做稳定的进动,而是以其进动角速度和章动角速度均周期性振荡变化的规律“抖动”前进。
但在实际情况中,由于摩擦的存在,式(6)、式(7)中的振荡项将很快衰减为零。去除振荡项之后的稳定值为
(8)
下面对此做出证明:
在章动很小的情况下,
(9)
稳定进动角动量的大小为
(10)
可见二者大小相等,但方向相反。
因此,实际情况应该是这样的,水平释放后陀螺开始抖动着前进,稳定后其悬空端会稍微向下倾斜,使自转角动量L有一个向下的分量抵消了进动角动量,从而保证了竖直方向角动量守恒。
2 阻尼条件下的动力学分析
为了弄清实际陀螺进动从开始到稳定的过程,我们考虑有阻尼的情况,其主要来自于陀螺转动时与支架的摩擦。类似于运动物体在空气中运动受到的阻力在速率不高时为f=-k,k为阻力系数,转动中摩擦产生阻尼力矩,大小与角速度成正比,方向相反。即,Mr=-krω;kr为转动阻尼系数。然而,一般情况下进动阻尼远小于章动阻尼。忽略进动阻尼,只考虑章动阻尼后,式(2)、式(3)保持不变,但式(4)改写为
(4a)
式中kn为章动阻尼系数。化简可得
(5a)
同样,上式联立式(3),结合初始条件可得有章动阻尼时的进动角速度ωp和章动角速度ωn的大小
(11)

这即是引入章动阻尼时,关于陀螺运动的一个较为精确的解。图4是考虑章动阻尼时P点空间轨迹的数值模拟结果。如图4所示,为保证系统竖直方向的角动量守恒(恒为零),从水平位置P(t=0)释放后陀螺开始抖动着进动,稳定后其悬空端会稍微向下倾斜至P′,使其自转角动量L有一个向下的分量正好抵消进动角动量。
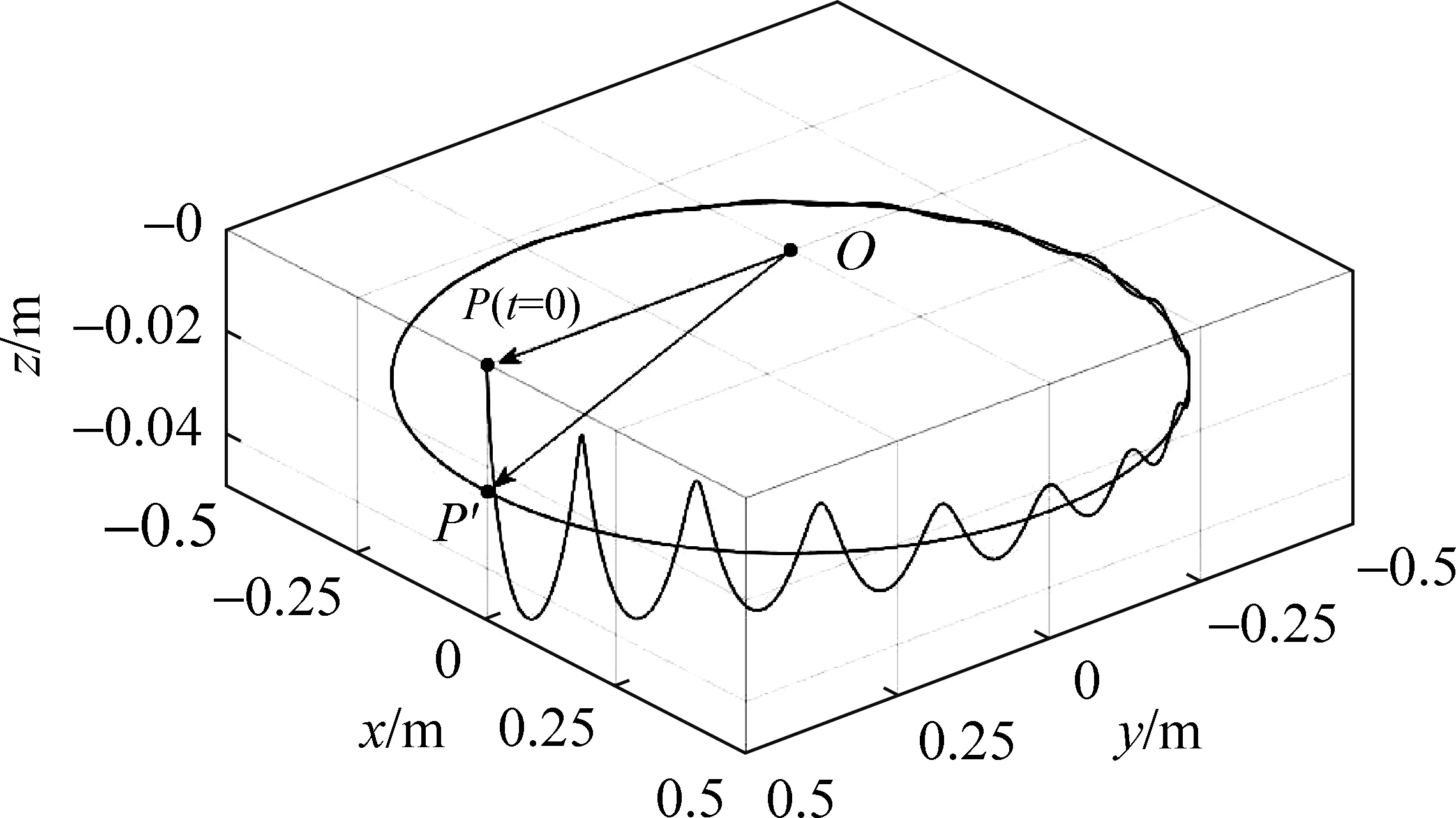
图4 章动阻尼下陀螺仪悬空端P点空间轨迹
3 全阻尼情况讨论
实际上摩擦也会产生进动阻尼,并且进动阻尼力矩沿竖直方向,使系统在竖直方向受到的合力矩不再为零,该方向的角动量也不再守恒。我们也对全阻尼情况作了计算,此时进动角θ随时间的变化关系为
(14)
式中kn,kp分别为章动和进动阻尼系数。章动角α随时间的变化关系
(15)

图5所示为全阻尼下陀螺仪悬空端P的轨迹的数值模拟结果。可以看出,摩擦逐渐消耗系统的能量,陀螺最终会“屈服”于重力,慢慢掉下去。只是一般演示实验中,由于重力力矩远大于阻尼力矩,几个进动周期内陀螺下落不明显。

图5 全阻尼情况下陀螺仪悬空端P的空间轨迹
4 结语
本文通过解析计算和数值模拟,系统研究了回转效应中的陀螺运动规律。首先考虑理想情况,发现水平释放后陀螺并不是作稳定的进动,而是以进动和章动角速度均周期性变化的规律“抖动”前进。实际情况,由于摩擦,抖动会逐渐消失,稳定后陀螺下倾,使自转角动量有一个向下的分量抵消了进动角动量,从而保证了竖直方向角动量恒为零,解释了进动演示实验中由于进动角动量出现导致的看似竖直方向上的角动量“不守恒”问题。进而为了弄清陀螺从水平释放达到稳定的动力学过程,我们逐步在模型中引入章动和进动阻尼,并详细分析了陀螺在阻尼条件下的运动行为。

