简论初中数学课堂中学生猜想能力的培养

猜想是思维训练的一种有效途径，它是通过人们对生活的见解，并加上自身的经验、感觉等推理出的可能性结论，在学习数学的过程中合理运用猜想能力可以起事半功倍的效果。新课程改革背景下，培养学生的猜想能力一方面是创新型人才的必备条件，另一方面是学生学习数学的需要。因此，教师在教书育人的同时应注重培养学生的猜想能力，帮助学生理清思路，使学生通过猜想进一步求证答案，给出证明或是举出反例，实现培养学生猜想能力的目标。

一、巧设规律性问题，激发猜想兴趣

近些年，中考试题中常出现的一种题型为规律性问题，目的在于考核学生的观察、分析及归纳能力。规律性题型不仅有利于教师掌握学生学习数学的情况，同时有利于高一级的学校选拔优秀的人才。在初中数学课程中，常出现的规律性题型分别有：与数列有关的规律，与图形有关的规律及与平面直角坐标系有关的规律等。教师要善于抓住这种规律性题型，巧设规律性问题引导学生进行猜想，在猜想的过程中激发学生的猜想兴趣，并拓展学生的思维，促使学生的思维与观察能力得到均衡发展。以一道中考数学题为例：图1的正六边形分割后可得到图2，将图2中最小的正六边形分割后可得图3，再将图3的最小的正六边形进行分割……则第n个图形中，一共有___个正六边形？

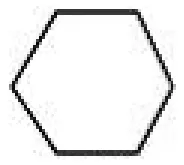
图1

图2

图3

学生仔细观察这道题后就会发现一个规律：图1是1个正六边形，图2是在图1的基础上添加了3个正六边形，图3是在图2的基础上添加了3个正六边形。因此，教师可以根据这一规律指导学生通过三个图形中正六边形的数目分析数据特点，接着根据这些图形进行猜想：如果每分割1次，正六边形增加则3个，那么第n个图形应是 “3n-2”个。教师巧设规律性问题，而学生通过对规律性问题进行猜想，很容易就能发现题目中已经给出的条件，有利于学生利用条件解开难题。学生可以通过这种方式观察、比较每个图形，同时将图形问题转变为数量问题，接着开动脑筋去思考，更容易理解其中的概念，由于难度已经相对降低，学生的猜想兴趣也会得到激发。

二、创造问题情境，锻炼猜想思维

教师可以抓住初中生好奇心强的这一特点，有目的、有意识地为学生创设不同的问题情境，并且灵活运用于课堂，吸引学生的目光，让学生全身心参与课堂学习，促使学生发现问题、解决问题，跟上教师的思路学习新知识，从而提高数学成绩。以 “平行四边形”一课教学为例，教师可以利用多媒体设备向学生展示一个四边形与平行四边形的模型，让学生观察两个图形的区别，然后展示四边形演变为平行四边形的过程，最后提出问题： “平行四边形和四边形之间有什么联系？通过运用多媒体设备演示四边形演变为平行四边形的过程，你从中发现了什么现象？”教师向学生提供相对简单的学习材料，这样很容易让学生陷入沉思，有个学生对此进行了猜想： “首先平行四边形是四边形，并具有四边形的一般特性，从平行四边形的对边来看，平行四边形即特殊的四边形，说明它有着专属的特殊性质。”通过创设问题情境，指引学生深入研究教材内容，在探究的过程中大胆猜想，并且寻求证据验证猜想，有利于学生掌握教材知识。需要引起注意的是，教师的提问必须与教材内容有关联，具有针对性与连贯性，使教师传授的知识环环相扣。

三、利用多媒体设备，培育猜想能力

如今，网络技术飞速发展，教育手段不断提高，多媒体设备也在学校中得到广泛应用。多媒体设备教学的最大优点是可以改变教师仅靠一支粉笔、一张嘴进行教学的局面，可以将枯燥乏味的教材内容变为图文并茂的内容向学生展示，同时将课堂氛围变得充满趣味、生动活泼，让学生产生学习的兴趣，容易理解与掌握所学知识。因此，教师要充分利用多媒体设备，适当转变教学方式，调动学生的积极性，在提高学生成绩的同时培育学生的猜想能力。以 “多边形的内角和与外角和”为例，教师可以利用多媒体设备引导学生对多边形的内角和与外角和进行探究。教师在多媒体上展示三角形、四边形、五边形等，向学生提问 “经过它们的顶点可以引出几条对角线，同时又能将多边形分成几个三角形？”然后指导学生动手操作。教师在多媒体上演示，待学生发现其中的规律后，就可以马上引入本节课的知识，学生保持着高度的热情及时进入学习状态，能够很好地吸收与消化教师传授的知识。通过这种方式形成悬念，充分唤起学生的好奇心，此时教师再指引学生展开思考、探索未知，达到培育学生猜想能力的效果。

四、借助数学练习题，巩固猜想能力

数学学习没有捷径，只有保证做题的数量与质量，才能一步步地学好数学。日常生活中普遍出现一种现象：学生在解题过程中没有解题的思路，或是解题思路中断。而出现这种现象的原因多数是学生没有牢牢掌握所学的知识，同时在做题时因为题目中缺乏引导性材料，学生无法理解题目表达的意思、给出的条件，从而失去解题的耐心。因此，在学生解题过程中，教师需要指引学生分析习题中给出的条件，提示学生发现题目中的已知与未知关系，并根据自己的经验猜想出答案，以此不断拓展思维。

譬如， “你可以比较20162015与20152016的大小吗？”这一道题目主要考察学生的猜想与探索能力，学生在思考两个数的大小时，如果盲目猜想很可能会对答案感到茫然。此时，教师可以提示学生从简单的情形入手，发现规律后再猜想结论，这样就可以降低习题的难度。可以将原题分解为几个小步骤： （1）请你计算下列每组中两个数的大小：①12__21②23__32③34__43④45__54⑤56__65。 （2） 根据上题的计算结果，试着猜想n（n+1）与 （n+1）n的大小关系为___。 （3）结合上两题猜想得到的结果，比较20162015与20152016的大小。教师的提示帮助学生找到突破口，此时学生仿佛茅塞顿开，通过猜想找到了题目的规律，同时想象力与观察能力也得到提升。教师在培养学生猜想能力的一系列过程中，需要注意几个问题： （1）猜想要同验证结合，没有经过验证的猜想属于空想，毫无意义。因此，在学生猜想的过程中，教师要提示学生寻求证据去验证，从而促进猜想能力与判断能力的提高。 （2）学生的猜想不可能全是正确的，有时候其想法比较稚嫩。教师应时刻注重培养学生的猜想能力，对于学生的猜想应以鼓励为主，保护学生的积极性，让学生在猜想中不断进步。

总之，教师的职责不仅是教书，将毕生所学毫无保留地传授给学生，还要注重学生的全面发展，让学生在猜想中不断思考，培养学生的猜想能力，促进思维能力的提升。