以学材设计为抓手,引导学生走出认知误区
——以“三角形的面积”教学为例
江苏海门市货隆小学(226144)
学生在日常生活中逐步形成的前概念与科学的概念往往大相迳庭,由此就产生了认知误区。作为教师,要在学生的认知基础上,选择有效的学习材料,对学生进行纠正和引导。笔者通过研究发现,学习材料的选择和设计是一个非常重要的环节。因此,教师应找到学生出现认知误区的原因,并以学材设计为抓手引导学生走出认知误区。下面以“三角形的面积”的教学为例进行探讨。
一、典型学材的设计误区及缺陷分析
典型的学材设计1:给学生提供3个三角形。
教师给学生提供3个三角形,让学生结合原有的经验进行操作,通过这个学材的使用,把学生的思维从“把一个三角形沿高剪开来拼”调正到“用两个完全相同的三角形来拼”,学生的思维也能从只会转化等腰三角形调正为能够转化任意三角形。但此学材设计存在的误区也是很明显的,当学生面对三角形无法转化成功的情况时,教师让学生从“三角形可以分为两个完全一样的三角形”这个原有认知调正到“两个完全一样的三角形,才能拼成平行四边形”,过程太过生硬,学生无法调动原有的拼接经验,不能独立寻找到“倍拼法”。在这个过程中,教师的探究方式又比较单一,学生的探究主动性没有被充分调动起来。
典型的学材设计2:给学生提供以方格图为背景的直角、锐角、钝角三角形图形各一个(如图1)。

图1
大部分教师都是先让学生尝试求直角三角形的面积,然后得出直角三角形的面积等于两条直角边的积除以2。而在研究锐角三角形的面积时,则将锐角三角形看成是两个直角三角形“”,再将较大的直角三角形分割、旋转“”,形成平行四边形。最后再引导学生完成钝角三角形面积公式的推导。
这个学材的设计,使学生能够在方格图中用“中位线割补法”完成“倍拼”的构想,将三角形转化成已学过的图形,因此推理出三角形的面积计算公式。然而,这一学材设计由于是从直角三角形出发到锐角三角形再到钝角三角形的尝试探究,整个过程比较繁杂冗长,探究的背景也始终都是在方格图中,导致学生在面对没有任何数据背景的任意三角形,需要测量数据时,就束手无策。
典型的学材设计3:给学生提供以平行四边形为背景的一个直角三角形ABE(如图2)。

图2
这个学材设计是借助平行四边形和直角三角形之间的特殊关系,让学生完成“加倍”的认知,从计算平行四边形中直角三角形的面积出发去推导三角形的面积计算公式,从而逐步完成任意三角形的面积计算公式的推导。这样使用学材设计的推导方式比较单一。
二、学材设计的调正策略及设计意图分析
学材设计片段一:
先给学生出示直角三角形和方格图。直接追问学生怎么算三角形的面积,需要什么数据条件。根据学生的反馈,再给学生提供一整张以方格图为背景的A4纸,纸上印有3个三角形,让学生有创作的空间。
[设计意图]这样设计学材,是基于两个方面的考虑:其一,直接向学生提出研究的内容,大部分学生在看教材、做作业的过程中,发现了公式,并能够运用公式来进行面积计算,学生由此发现这节课并不只是研究怎么算,而是重点研究为什么这样算,这给本堂课注入了核心的思考力。其二,给学生提供方格图,能够让学生对照具体数据,研究其中的数理,这让学生面对底和高这些抽象的名称时更容易说理和分析。
学材设计片段二:
提问:“三角形的面积公式中为什么要除以2?”学生展开讨论,有的认为从三角形的中位线割开,通过旋转拼成一个长方形,这个长方形的长与原来的三角形的底一样,但它的宽是原来三角形的一半,因此高需要除以2。也有学生认为将三角形转化成长方形之后,底边只有原来的一半,所以底边要除以2。在这个环节中,笔者向学生直观呈现中位线割补的动态过程,让学生直观看到怎么样切割才能够拼成平行四边形或是长方形。(如图3)

图3
学生由此认识到,将三角形转化成平行四边形或者长方形,需要沿着三角形高的中点到斜边的中点或从底的中点到斜边的中点进行分割,将高割掉一半或者是将底边割掉一半来拼成学过的平行四边形或者长方形。
[设计意图]这一学材是根据学生的经验来进行设计的,此设计以方格图为背景,使学生能够利用割补转化的方法将单个直角三角形直接分割转化为已学过的平行四边形或是长方形,促使学生轻松理解三角形面积公式的本质内涵。
学材设计片段三:
给学生直观呈现一个平行四边形,已知平行四边形的面积是6平方厘米,要求学生观察思考:能否从平行四边形中看到三角形?学生认为,平行四边形的对角线能将其等分成两个三角形,三角形的面积是平行四边形面积的一半。紧接着,又给学生一个“单身”的三角形,要求学生找到“单身”三角形的“伙伴”——平行四边形(如图4)。
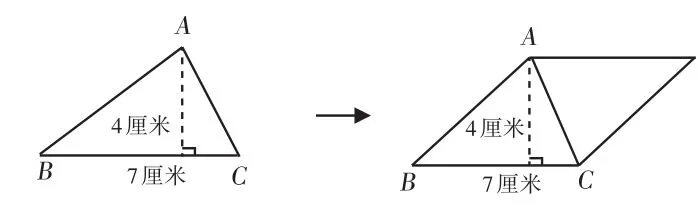
图4
[设计意图]设计这样的学材,有两个方面的目的,一是强化学生的直观感知。先让学生将一个平行四边形分割成两个三角形,然后再从单个的三角形去想象拼成的平行四边形,这样配合动态直观的感知过程,能够让学生进一步内化数学知识。二是通过故事化的语言,让学生牢牢记住三角形的“好伙伴”是平行四边形。在后续的练习中,学生加深了对“÷2”的印象,感受到“底乘高”算的是平行四边形的面积,要“÷2”才是三角形的面积。
综上可知,教师要以学材设计为抓手,调正原有认知和最终认知之间的差异。只有这样,才能够让学生经历从不完整的原有认知到构建完整认知的过程。这样的过程正是学生数学能力发展的过程,也是提升学生数学思维能力和自主探究能力的根本所在。

