浅谈基于目标的模块化教学设计——“解决问题的策略——列举”的教学与反思

江苏南京市天妃宫小学（210011）

模块化教学模式是在汲取模块化思想的基础上，将学科知识分解成一个个知识点，再将各知识点按其内在逻辑组合成相对独立的模块（单元），先定目标，再定内容，目的性强，教学效果显著。为此，我在教学苏教版教材五年级上册“解决问题的策略——列举”时，进行了一些有益的尝试和探索。

【模块一】激活经验，初步感知列举

师：10可以分成几和几？你用什么方法？

生1：可以把和是10的算式都写出来。

生2：我用列举的方法。

师：你是怎样列举的？

生2：我想10可以分成5+5、1+9、7+3、2+8、6+4。

生3：9+1、8+2、7+3、6+4、5+5。

生4：1+9、2+8、3+7、4+6、5+5。

生5：我觉得生2的方法有点乱。

生6：我认为生3、生4的方法都可以，但是我更赞成生4的方法。

师：说说你们的理由。

生5：因为这样列举很有序，我喜欢从小到大来找。

生6：我认为有了顺序，才不会遗漏。

师：像生3、生4这样按照一定顺序进行列举，就是有序列举。通常我们从小到大进行列举，这样列举的好处是不重复、不遗漏。

【反思】“10可以分成几和几”是一年级的知识。通过解决这个问题，让学生在交流互动中初步感知什么是有序列举，有序列举的方法以及注意事项，感受有序列举的好处——列举结果不重复、不遗漏。

【模块二】自主探索，亲身体验列举

师（出示例1：王大叔用22根1米长的木条围一个长方形花圃，怎样围面积最大？）：从题中你获得了哪些数学信息？

生1：22米是围成长方形的周长。

生2：长和宽的和是11米，而且长和宽都是整米数。

生3：长和宽都不确定，所以围的方法有很多种。

师：你们准备怎样解决这个问题？

生4：我把所有的围法一一列举出来，再比较，找到面积最大的围法。

生5：

宽/米长/米面积/平方米1 10 10 2 9 1 8 3 8 2 4 4 7 2 8 5 6 3 0

师：你是怎样列举的？又是根据什么来列举？

生5：我从宽开始列举，因为宽比长小；根据长和宽的和是11米来进行列举。

生6：为什么你列举到长6米、宽5米时就停了？

生5：因为再往后列举就和前面的重复了。

生7：

长/米宽/米面积/平方米1 10 10 2 9 1 8 3 8 2 4 4 7 2 8 5 6 3 0

师：列举时，你先列举的是什么？

生7：我从长开始列举。

生8：长比宽还短吗？

生7：我认为长和宽是相对的（一边说一边用长方形纸比画着）

师：生5和生7列举的相同点是什么？

生9：都是按照从小到大的顺序列举的，而且长和宽的和都是11米。

生10：都是列举到长6米、宽5米或长5米、宽6米时就停止了。

师：这样列举有什么好处？

生11：不重复、不遗漏。

【反思】让学生在解决问题中经历一一列举的全过程，体会有序列举的方法“一般从较小的量开始列举，这样可以使结果不重复、不遗漏”，感受有序列举的好处，同时让学生明确“理解题意”是解决问题的关键。

【模块三】回顾整理，完善列举建构

师：回顾解决问题的过程，你有什么体会？

生1：先要弄清题意，明确已知条件和所求问题。

生2：确定解决问题的方案，也就是解题策略。

生3：例1要用列举策略来解决。

师：你为什么用列举策略？

生3：因为只有把所有的围法一一列举出来，再比较，才能找到面积最大的围法。

师：在进行列举时，需要注意些什么？

生4：列举一定要有顺序，一般从较小的量开始列举。

生5：还要根据题意，找到要列举的量。

生6：有序列举出现重复情况时，就不能再往后列举了。

师：列举结束后，还要做什么？

生7：要检查列举的情况是否有重复或有无遗漏。

生8：根据列举的情况计算结果。

生9：根据题意，认真分析列举的结果，找到需要的答案。

【反思】通过回顾整理解决问题的全过程，概括、归纳出“在列举前应弄清题意，明白需要列举什么，根据什么进行列举”，从而掌握有序列举的方法。

【模块四】解决问题，体会列举价值

师：一张靶纸共三圈，投中内圈得10环，投中中圈得8环，投中外圈得6环。小华投中两次，可能得多少环？

生1：我先列举投中的两次中环数不同的，有3种情况，再列举投中的两次中环数相同的，也有3种情况，所以一共有6种不同情况。

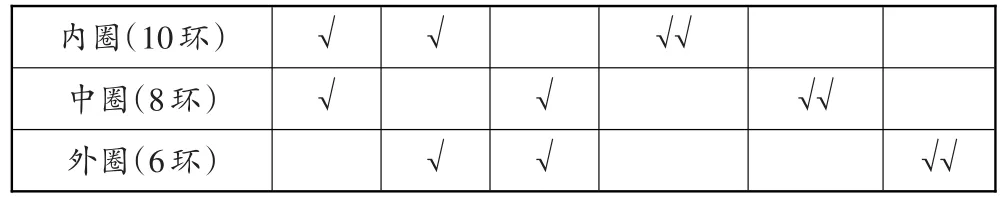
√√内圈（10环）中圈（8环）外圈（6环）√ √√ √√√√ √√√

生2：我是用算式列举的。10+10=20，8+8=16，6+6=12；10+8=18，10+6=16，8+6=14。我还发现10+6和8+8的结果相同，都是16环，所以这两种可能只能算作一种结果，因此一共有5种结果。

师：你是按什么顺序列举的？

生2：我是分类列举的，先列举投中环数相同的两次，再列举投中环数不同的两次。

师：对生1和生2的解答，你们如何评价？

生3：我赞成生2的。她用算式列举出6种情况，算出结果，再根据题意选择答案。

生4：我认为生1用列表方法列举的6种情况是对的，但没有对结果做出判断，不符合题意。

师：你们从中能得到什么启示？

生5：列举一定要有顺序。

生6：不仅要有顺序，还要根据题意对列举的结果进行判断和选择。

师：生1和生2在解决问题时有什么相同之处？

生7：都是有序列举。

【反思】通过解决实际问题，使学生理解列举策略呈现形式虽然不同，但本质都是一一列举，体会列举策略的价值，同时，渗透具体问题要具体分析的辩证思维，发展学生的数学思维。

【教学思考】

1.有效导入是实现教学目标的前提

没有欢欣鼓舞的心情，学习就会成为学生沉重的负担。因此，课堂导入既要能引起学生的学习兴趣，又要能围绕知识结构建立新旧知识之间的联系，这样的课堂导入才是丰富和有效的。

本节课从“10可以分成几和几”这个学生熟悉的问题开始，让学生从心理上感到亲近，正确的解答又能使学生心情愉悦，快速建立学习本课知识的自信心。虽然学生没有正式学习列举，但是已经在使用列举方法解决简单的问题，这个导入的目的不仅是解决10可以分成几和几的问题，更是让学生通过解答几加几等于10的过程，知道什么是列举、列举的方法以及列举需要注意些什么等，为实现本节课教学目标做好铺垫。

2.经历过程是实现教学目标的关键

课程标准指出：“学生是学习的主体，教学过程中教师要依据学生的年龄特点和认知水平，设计探索性和开放性的问题，给学生提供自主探索的机会。”

本课的例题具有较强的探索性。首先，要想知道怎样围面积最大，就需要将所有的围法全部列出来；其次，思考根据什么进行列举，长方形的周长是22米，则长与宽的和就是11米，从中就能发现列举的依据；对于怎样进行列举，一般应从小到大列出所有的情况，这就是有序；最后计算每一种围法的面积，得出怎样围面积最大。这里的每一步都是学生在自主探究中获得的，学生在亲身体会为什么要进行有序列举，怎样进行有序列举，体验有序列举的价值，真正实现教学目标。

3.回顾反思是实现教学目标的保证

回顾和反思是建立和完善学生知识结构的重要环节，是对已学知识进行整理提升的过程，有利于发展学生的数学思考能力，提高学生的应用能力。

本节课始终围绕列举的探究过程，以问题引领学生进行回顾反思。通过“解决问题（例1）的过程，你有什么体会？在进行列举时，需要注意些什么？列举结束后，你还要做什么？”引导学生反思：列举前，要找到列举的依据；列举中，要使列举有一定顺序；列举后，要对结果进行分析和处理。至此，加深了学生对所学知识的理解，培养了学生运用列举策略解决实际问题的能力，达成教学目标。

总之，在课堂教学中，通过模块化的教学设计，可以细化教学目标，使每一模块目标明确，思路清晰，同时各个模块之间又互相联系、相互影响。经过分层实施，分步操作，落实好每一模块的教学目标，就能提高课堂教学的有效性，提升学生的学习能力。