钢管混凝土拱桥静力特性研究

丁峥时 卢 波

（江苏省无锡交通高等职业技术学校 214151）

1 工程背景

本文以张-唐段（张家口-唐山铁路路段）工程通用设计建设的一座下承式简支拱桥为研究对象。工程位于石家庄与张家口之间的一条铁路上，起点桩号K1+650，终点桩号K1+655，拱桥建模选取的是杆件模型，桥主梁部分类似于鱼骨架结构，即主梁为单根杆件，在其两侧延伸出5组刚臂分别与拱桥的吊杆和拱连接，只起到传力作用。

该桥采用拱脚与桥墩完全分离的简支下承式柔性系杆刚性拱，拱的主拱材料为钢管混凝土，此钢管混凝土拱桥的跨度为5.0m，宽度为10.08m，桥面厚度为0.5m。拱架截面为圆形，钢管外径为0.2m，共5对10根吊杆。图1为钢管混凝土拱肋桥的简易模型（图中单位为mm）。

2 结构特点

大跨度无推力的下承式钢管混凝土简支拱桥，其设计构思是在该拱桥两拱脚下设置支座，在两拱脚之间设置强大的系杆以平衡拱的水平推力，这样该拱桥和简支梁桥一样没有水平推力，属于内部超静定而外部静定的结构体系。故此该桥型具有拱桥的较大跨越能力和简支梁桥对地基及温度变化适应能力强的双重特点，而且还具有建筑高度低、受力合理、能够充分发挥不同材料的优势、建筑材料用量相对较少和施工速度快等优点，在沿海软基、平原地区是具有较强优势的一种桥型。

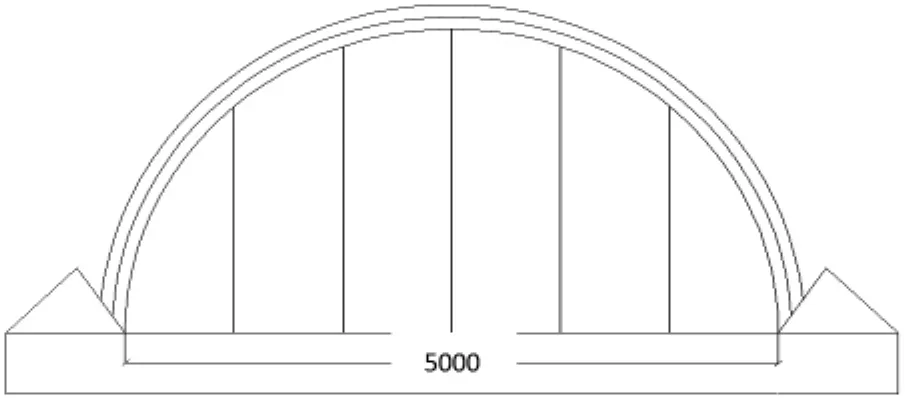
图1 拱桥简图

3 材料参数

拱桥的几何模型建立完成后，就要对其进行材料属性进行定义以及网格划分，转化为有限元模型（见图1）。首先，对桥的主梁部分，要采用beam单元并定义其横截面是一个矩形，高宽分别为2m和10.8m。不记其内配置的普通钢筋，所以将其等效成C50混凝土材料，弹性模量为3.45E10Pa、泊松比为0.2和密度为2500kg/m3。桥主梁两侧延伸出的刚臂，也采用beam单元，并定义弹性模量为3.45E13Pa，因为刚臂部分只起到主梁与吊杆之间的传力作用，其变形可以忽略，因此泊松比和密度均定义为0。

4 钢管混凝土拱肋的施工

该拱桥的钢管混凝土拱肋施工时，采用的施工流程为：搭设拱肋安装支架→铺设运送拱肋轨道→吊装拱肋→吊装风撑→焊缝探伤→灌注两侧拱脚混凝土→拱肋内浇筑填充混凝土→安装吊杆→吊杆张拉，封端→拱肋填充混凝土密实度检测→拱肋油漆。

5 材料应力-应变关系

钢管和混凝土在共同受力承受荷载作用时，两者之间的相互作用机理是非常复杂的。为了能够更好的模拟两者的应力-应变关系，本文引入了钢材和混凝土的应力-应变关系。其原理就是先分别确定钢管和混凝土的应力-应变关系曲线，然后利用数值方法对两者的应力-应变关系曲线进行耦合，将耦合得到的曲线作为钢管和混凝土共同作用时的综合曲线，然后推导出两者的组合刚度和组合模量。

为了方便计算钢管混凝土的刚度矩阵，我们用综合应力-应变关系将钢管混凝土的力学性能指标统一为组合性能指标。该指标根据下列步骤获得：

（1）分别导出钢材和混凝土这两种材料在多轴应力状态下本构关系的数学表达式；

（2）利用有限元方法得到钢管混凝土在各种应力状态下的荷载-变形关系曲线；

（3）根据得到的关系曲线，确定极限准则，定出承载力组合设计指标，如图2所示。

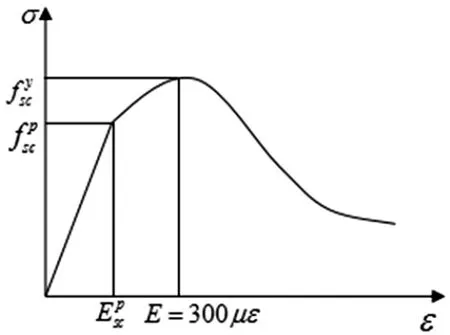
图2 应力-应变曲线

由图2可知，钢管混凝土轴心受压时表现很好的弹性和塑性性能，可把全过程曲线分成弹性、弹塑性和强化三个阶段，强化阶段的斜率主要取决于含钢率大小，含钢率大时斜率大，强化程度高；反之，则较低。

6 恒载作用下拱桥力学性能分析

6.1 拱桥的挠度分析

完成对拱桥的有限元建模后，接下来要考虑拱桥的自重和二期恒载的影响以及如何施加在拱桥上。首先，对于拱桥的自重，在建立拱桥有限元模型时，定义了拱桥各部分材料的材料属性，只需在MATLAB命令流中加入重力加速度即可完成拱桥的重力施加。而拱桥的二期恒载的施加需要特别考虑。拱桥的二期荷载就是在桥梁主体完成建设后在桥面上铺装的附属设施重量，包括人行道板以及沥青路面等等。通常这一部分荷载可以以均布荷载的形式施加在拱桥主梁上，其大小在拱桥的设计图纸上已经给出，为107kN/m。

6.2 拱肋轴力分析

相比于主梁的弯矩和挠度，拱肋的弯矩非常小，几乎可以忽略不计，但是拱肋的轴力很大，且由于拱肋每一点的轴力值都不相同，所以本节中只对几个特殊位置的拱肋单元所受的轴力进行了分析。由于拱桥的对称性，两条拱的受力状态相同，所以只需研究一条拱的轴力状态即可。

6.3 吊杆内力分析

对于简支拱桥，吊杆的安装是有一定的预张力的，吊杆在经过张拉之后安装在拱桥主梁与拱之间，使得桥拱能更好的帮助主梁分担一部分荷载。吊杆在选取单元类型时，采用的是link单元，所以，在设置吊杆材料实常数时加上吊杆预张力对应的应变作为初应变，即可在拱桥模型中对吊杆实现预张拉。

7 小结

本章主要对拱桥在恒载，桥梁、拱肋以及吊杆的内力和变形进行了分析研究。指出了在恒载作用下主梁，拱肋以及吊杆内力和变形的最大位置以及在静活在作用下主梁、拱肋及吊杆内力最大值的变化情况，具体成果如下：

（1）在横载作用下，拱桥的变形相对于跨中是对称的，其中跨中的竖向挠度最大，向两端逐渐变小。跨中最大挠度为20mm，这与理论计算结果的20.3mm是非常接近的，说明建立的模型与理论情况是相符的。

（2）拱肋的轴力主要为压力，相对于拱顶是对称的，其中位于拱顶的轴力最小值为13320kN，拱肋两端的轴力最大为15990kN。最大值与最小值相差16.7%，因此在进行拱桥设计时，要考虑拱肋两端桥墩的抗压强度是否能够满足要求。