燃气流场算法程序实现及对比

王 帅，陈劲松

（北京航天发射技术研究所，北京，100076）

0 引 言

近年来随着计算机技术的发展，数值模拟已成为燃气流场研究的重要手段，在航天领域有着广泛应用。通过数值模拟方法能够掌握燃气流场的流动特性和场内结构的力热环境，并且高精度的燃气流场数值模拟技术是燃气流场噪声仿真的基础，所以选取更适合燃气流场模拟的计算格式，提高燃气流场数值模拟的准确性和计算效率，具有重要的意义。

因计算流体力学（Computational Fluid Dynamics，CFD）商业软件所提供的计算格式有限，要综合比较多种计算格式只能通过编程实现，现选取计算格式中文献引用较多的 Roe格式、AUSM+格式与 NND格式[1～4]编写了燃气流场计算程序，完成了二维前台阶激波反射算例、三维喷管燃气内流场算例和三维燃气自由喷流流场算例的数值模拟。通过3种格式计算结果的对比分析，一方面能够总结燃气流场的流动特性，另一方面也能比较分析3种格式的特点和性能。

1 数值计算方法

程序采用有限体积法求解笛卡尔坐标系下三维Euler方程，其积分形式如下：

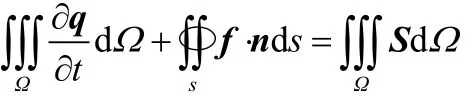
式中 q为守恒变量， q = [ ρ ,ρ u , ρ v, ρ w , ρ E ]T。f为对流通量，为单元网格体积；s为单元网格外表面；n为外表面微元法向单位向量；S为源项，在喷管流计算中源项为零。

根据有限体积法对上述方程在单元网格(I,J,K)上离散可得：

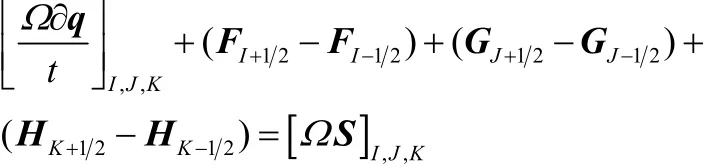
式中 下标“ I + 12”表示单元网格（I ,J,K） 上I方向正向面；“ I - 1 2”表示单元网格（I ,J,K） 上I方向负向面；F，G，H为各面上对流通量，数值上等于格心对流通量沿外表面法向分量与该面面积的乘积。

其中时间项采用显式三阶 Runge-Kutta法离散求解，而对流项分别采用3种迎风格式处理。为便于比较，将3种格式以一种统一形式表示：

式中 第1项可看作中心差分项，第2项为耗散项。所有矢通量均取 I + 12面法向面通量。线性近似系数矩阵 A (qˆ)、单元界面马赫数 M aI+12等特征参量在各计算流体力学书籍中均有提及，这里不再展开[5]。

本文 Roe格式属通量差分分裂（Flux Difference Splitting，FDS）格式，通过线性近似系数矩阵得到近似Riemann解，在具备高间断分辨率的同时也存在非物理解出现的可能性，所以在计算中需要加入熵修正条件，但熵修正也会引入额外耗散。在喷管流场计算中，选用Harten型熵修正。

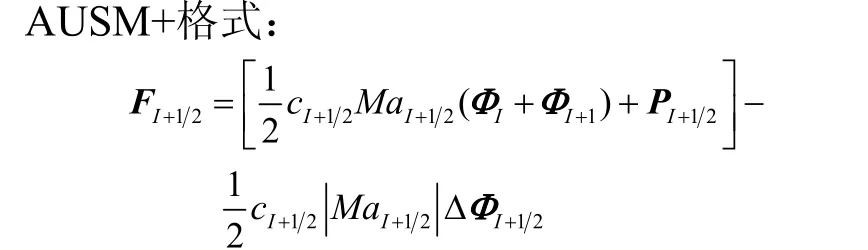
AUSM+格式将对流通量分裂为流动项Φ和压力项P分别处理，从耗散项分析，其耗散项系数在差分算子∆之外，类似于FDS格式，但其耗散项系数为标量形式，类似于矢通量分裂（Flux Vector Splitting，FVS）格式，所以 AUSM+可看作两类格式的复合形式，AUSM+格式数值耗散小，间断捕捉能力强，无需熵修正，也避免了大量的矩阵运算，具有较高的计算效率。

NND格式：

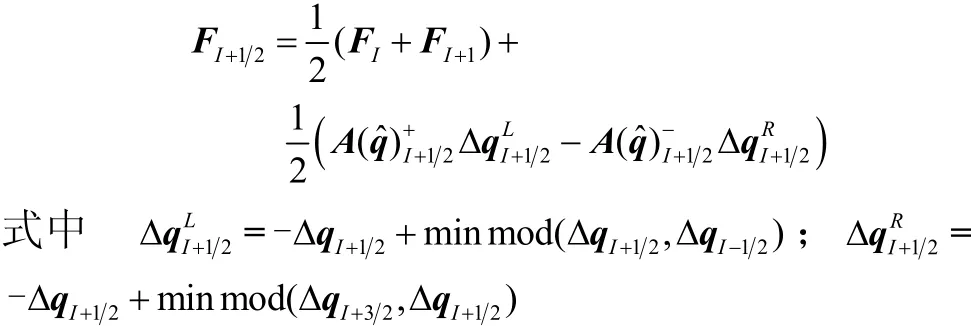
NND格式是由张涵信院士建立，具有TVD性质的、空间二阶精度的计算格式，在中国应用广泛。而在推广到三维有限体积法的过程中，发现原始的通量型NND格式效果不太理想，所以采用了一种类似FDS的迎风型NND格式[6]，该格式在计算中表现了更好的稳定性。

Roe格式与AUSM+格式本身为空间一阶精度，而NND格式为空间二阶精度，所以在Roe与AUSM+格式中采用MUSCL重构的方式将二者提高至二阶精度，同时引入Van Leer限制器避免MUSCL重构产生过大数值振荡。

2 算法程序验证

2.1 验证算例计算模型

前台阶激波反射流场是CFD研究中的经典算例，有充分的文献结果作为比对，能够验证计算程序的正确性，此算例采用无量纲化处理，计算模型见图1。

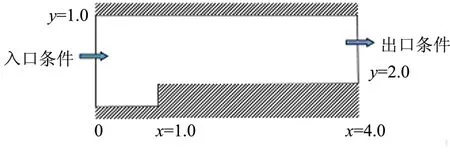
图1 前台阶流场计算模型Fig.1 Computational Model of Forward-facing Step Flow Field

计算网格为边长0.01的正方形网格。计算包含3类边界条件：左边界处为速度入口，固定来流马赫数为3。上下两面与台阶前面均为刚性壁面，满足滑移反射边界条件。右边界处为自由边界，满足自由输出条件。初始流场取自由来流均匀流场。

2.2 计算结果验证

文献[6]给出了Roe格式和 AUSM+格式的马赫数等值线图，文献[7]给出了NND格式的密度分布云图。程序计算结果与文献结果比对如图2至图4所示，其中横、纵坐标表示流场各点的位置坐标。

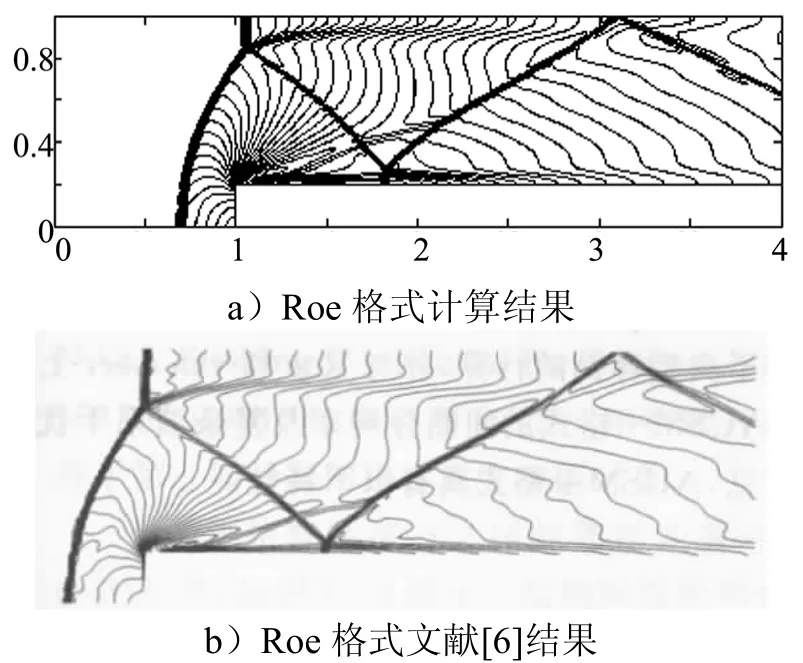
图2 Roe格式程序计算结果与文献结果对比Fig.2 Comparision of Simulation Result and Literature Result Using Roe Scheme

图3 AUSM+格式程序计算结果与文献结果对比Fig.3 Comparision of Simulation Result and Literature Result Using AUSM+ Scheme

图4 NND格式程序计算结果与文献结果对比Fig.4 Comparision of Simulation Result and Literature ResultUsing NND Scheme

从程序计算结果来看，3种计算格式能够清晰地捕捉到激波位置，且激波位置基本一致，表现出了良好的数值稳定性和激波捕捉能力。与文献结果对比来看，程序计算结果与文献结果基本一致，尤其NND格式结果非常吻合。而文献[6]所示Roe格式与AUSM+格式结果与程序计算结果相比具有较高的数值波动，这是由于文献所用限制器为superbee限制器，由此可见程序所用Van Leer限制器具有更明显的数值耗散作用，但同样能够清晰分辨整个流场结构。

通过与文献结果的比较，能够确认算法程序的计算结果是准确可靠的。之后通过喷管内流场和自由喷流的计算，详细比较分析计算格式在燃气流场计算中的特性。

3 喷管内流场模拟

3.1 计算模型

喷管内流场计算模型选取了某试验用直锥喷管，收缩半角为45°，扩张半角为18°。根据喷管的对称性，建立了双对称面的四分之一喷管网格模型，见图5。

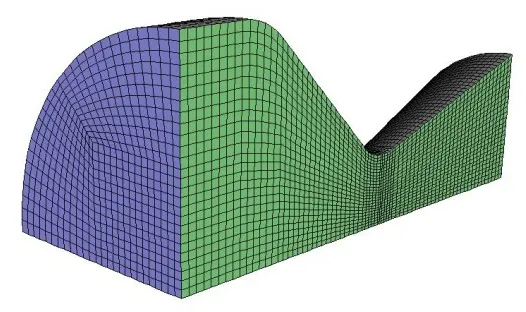
图5 喷管计算网格模型Fig.5 Computational Grid of Nozzle Flow Field

计算过程需处理4种边界条件：入口边界为压力入口，固定总压为5 MPa，总温为3000 K，速度方向垂直向内；出口边界分2种情况，当出口速度为超声速时，边界变量由内点插值得到，当出口速度为亚声速时，边界取环境压力，其余变量由黎曼边界条件得到；壁面边界为绝热光滑反射壁面；对称面边界满足标量法向梯度为零，垂直对称面的速度分量为零。

3.2 喷管对称面计算结果对比

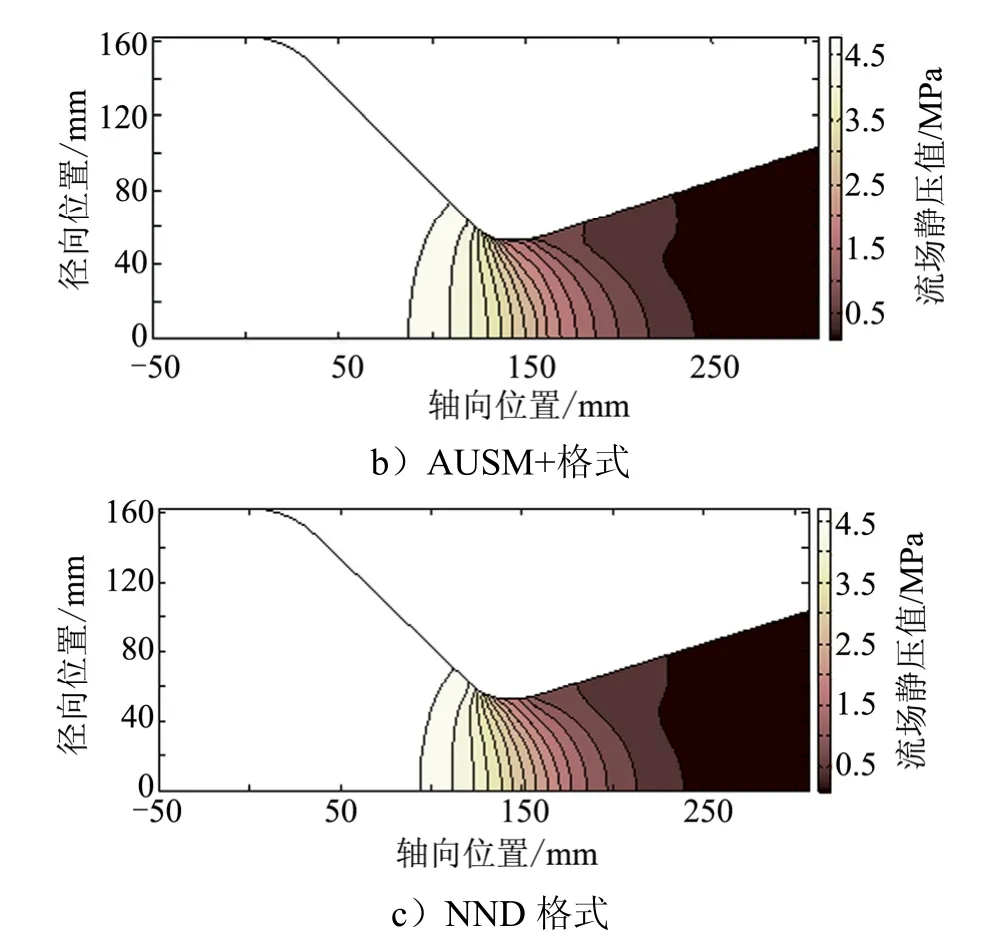
3种格式计算所得静压分布云图如图6所示。

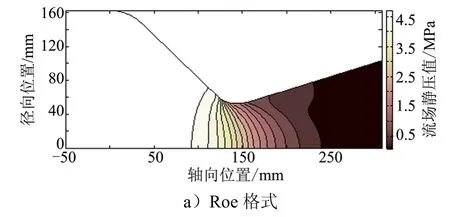
图6 喷管对称面静压分布云图Fig.6 Contours of Static Pressure at the Symmetry Plane of the Nozzle Flow Field

续图6

经比较可见，3种结果静压分布规律基本一致。管内静压沿轴线方向逐渐减小，且在喉部附近静压梯度最大。对比轴线与壁面静压，可见壁面静压在喉部变化更剧烈，且在喉部之后存在明显的低压区。3种格式计算结果在扩张段稍有差异，扩张段静压等值线存在一个凹陷，AUSM+格式与Roe格式捕捉的比较明显，而NND格式捕捉的较平缓。

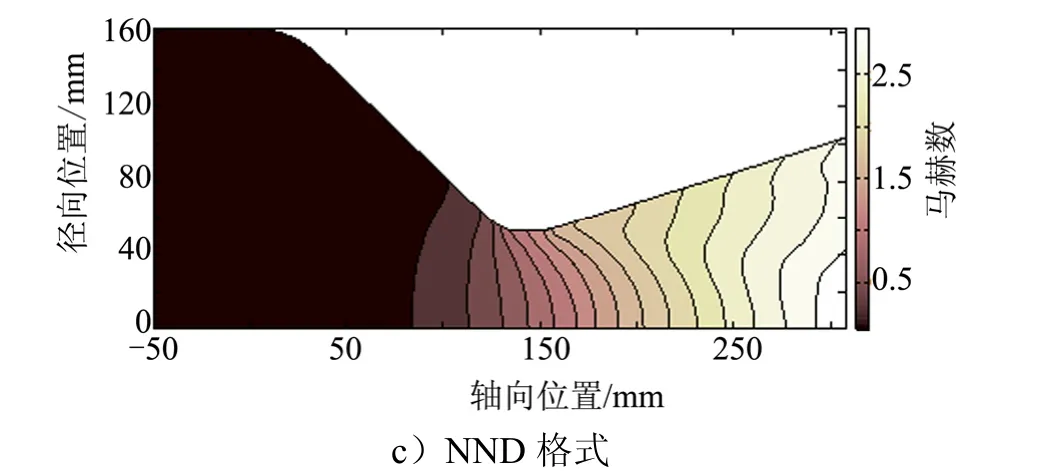
3种格式计算所得马赫数分布云图如图7所示。

图7 喷管对称面马赫数分布云图Fig.7 Contours of Mach Number at the Symmetry Plane of the Nozzle Flow Field

续图7

从整体看，三者所表现出的马赫数分布规律是一致的，马赫数沿轴线方向逐渐增大。3种格式在收缩段与喉部附近结果非常接近，而在扩张段存在细节上的差异，Roe格式所得扩张段等值线较平滑，无明显振荡，AUSM+格式等值线在壁面附近存在小幅震荡，而NND格式等值线在壁面附近同样产生了波动，但波动产生于扩张段后半部分，且越靠近出口越明显。

由图6和图7可见，3种格式在收缩段和喉部结果基本一致，主要差异存在于流动较复杂的扩张段，且马赫数差异较明显。为更细致的比较3种结果的差异，读取了喉部、扩张段中部和出口处沿喷管径向的马赫数分布，通过马赫数沿径向的变化详细比较3种格式的区别，并分析造成差异的原因。

3.3 沿喷管半径计算结果对比

3种计算格式在喉部、扩张段中部和出口处马赫数沿喷管径向的分布如图8至图10所示。

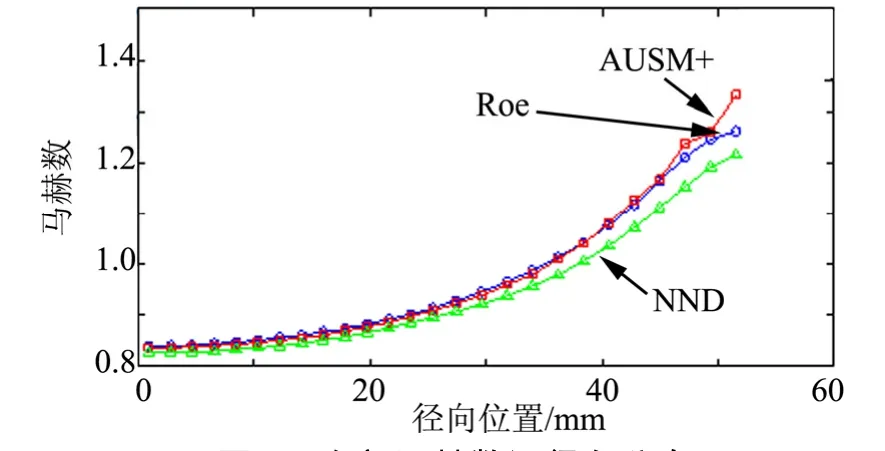
图8 喉部马赫数沿径向分布Fig.8 The Radial Mach Number Distributions at the Nozzle Throat

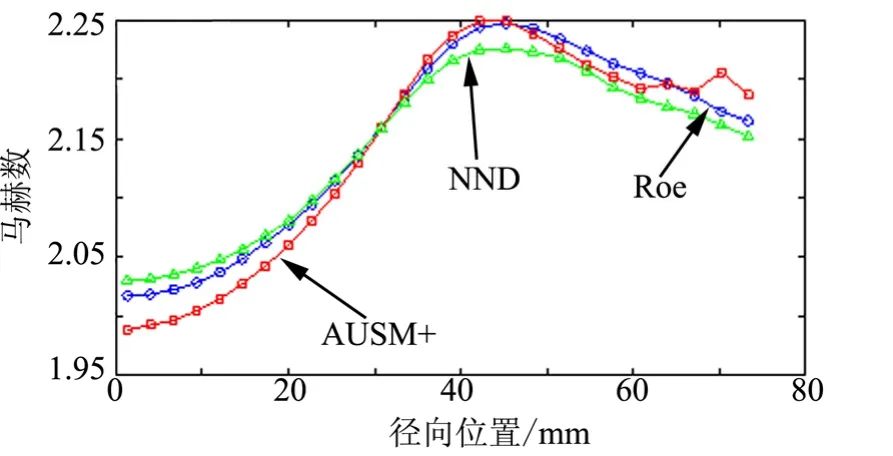
图9 扩张段中部马赫数沿径向分布Fig.9 The Radial Mach Number Distributions at the Middle of the Nozzle Divergent Section

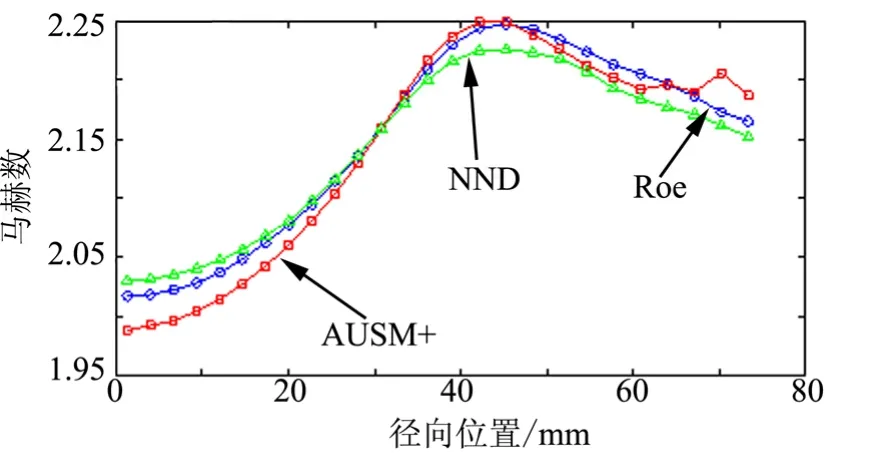
图10 出口马赫数沿径向分布Fig.10 The Radial Mach Number Distributions at the Nozzle Exit

首先分析3种格式计算结果的相同点：马赫数沿径向的变化规律基本相同。在喉部，马赫数沿径向向外逐渐增大，在壁面附近达到最大值；在扩张段中部，马赫数沿径向先增加后减小，在径向中段到达最大值；在出口处，马赫数沿径向先几乎不变，然后逐渐减小，在中段梯度最大，在壁面附近变化较缓。

下面着重比较3种格式之间的差异，Roe格式在3处截面所得曲线均较平滑，表现出了良好的数值稳定性；AUSM+格式在3处截面马赫数曲线壁面附近均存在数值振荡；而NND格式在喉部、扩张段中部曲线较光滑，而在出口处壁面附近存在较大波动。纵向比较来看，两种格式数值振荡产生的原因是不同的。

AUSM+格式在壁面附近均产生振荡，可见振荡是由壁面条件引起的。从格式本身来看，AUSM+的耗散项系数为标量形式，主要与单元界面马赫数相关，而根据壁面边界条件，壁面处流通量为零，再根据质量守恒，贴壁网格壁面的对面流通量也几乎为零，所以这两面的单元界面马赫数也近似为零，即在垂直壁面方向耗散项系数近似为零，所以可认为壁面附近网格计算中缺少了垂直于壁面方向的数值耗散，从而导致壁面附近产生了数值振荡。

NND格式只在出口附近的壁面处存在数值波动，且越靠近出口，波动越明显，可见波动主要由出口条件引起。虽然本文采用的是迎风型NND格式，但NND格式本身对正负流通量的处理仍分别采用迎风差分和中心差分，所以其受下游数据的影响程度要高于另两种迎风格式。流动达稳态时，出口处为超声速，数值上取出口边界为内点的插值，而对于真实流动，出口参数并不是简单的内点插值，这一误差对NND格式造成了更大的影响。

除去上述数值振荡的差异，3种格式在径向还表现出了变化幅度的差别，以扩张段中部处马赫数曲线最明显，AUSM+格式变化幅度最大，Roe格式次之，而NND格式变化幅度最小，且之前在对称面静压云图的比较中同样发现NND格式有较明显的抹平现象。既然3种格式同为空间二阶精度，那么可以认为这种幅值的差异主要是由格式不同的数值耗散造成的。相同条件下，3种格式中 AUSM+格式数值耗散最小，而 NND格式的数值耗散最大。

3.4 计算结果验证

一维等熵喷管马赫数曲线与3种格式喷管截面平均马赫数曲线比较如图11所示。

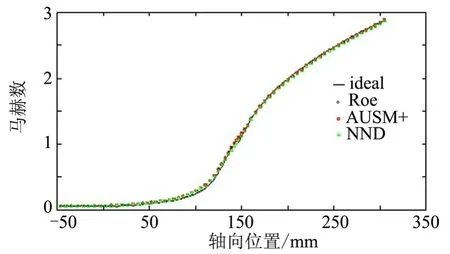
图11 一维等熵喷管马赫数曲线与截面平均马赫数曲线Fig.11 The One-dimensional Isentropic Nozzle Mach Number Distribution and the Average Mach Number Distributions

由图11可见，3种格式所得平均马赫数曲线与理论曲线基本一致，数值误差不超过马赫数为0.045，说明计算结果与理论分析结果是相符的。同时可以发现主要偏差出现在收缩段，这是由于喷管收缩段斜率较大，气流存在较大的径向速度分量，与拟一维流动状态存在较大差别。

另外，3种格式同样可以互为校验，经过之前的比较分析，除去格式本身特性所造成的差异外，3种格式的计算结果表现出了高度的一致性，彼此差异很小，这同样能够验证计算结果是可靠的。

4 喷管自由喷流流场模拟

4.1 计算模型

喷管自由喷流计算模型是在之前喷管模型的基础上加入外流场得到的，轴向计算范围由喷管出口前1 m到喷管后 10 m，径向计算范围为 5 m。网格模型如图12所示。

图12 自由喷流网格模型Fig.12 Computational Grid of Free Jet Flow Field

续图12

实际计算中发现5 MPa、3000 K的入口条件要得到稳定的外流场需要很长的计算时间，所以将入口总压降为1 MPa，总温降为2000 K。对自由喷流流场而言，只靠格式本身耗散难以得到稳定流场解，所以计算中加入了黏性耗散项和标准 -kε湍流模型。

4.2 计算结果对比分析

图13和图14分别给出了燃气自由喷流流场对称面静压分布云图和马赫数分布云图。图13中数值表示等值线上静压值，单位为MPa，图14中数值表示等值线上马赫数值。

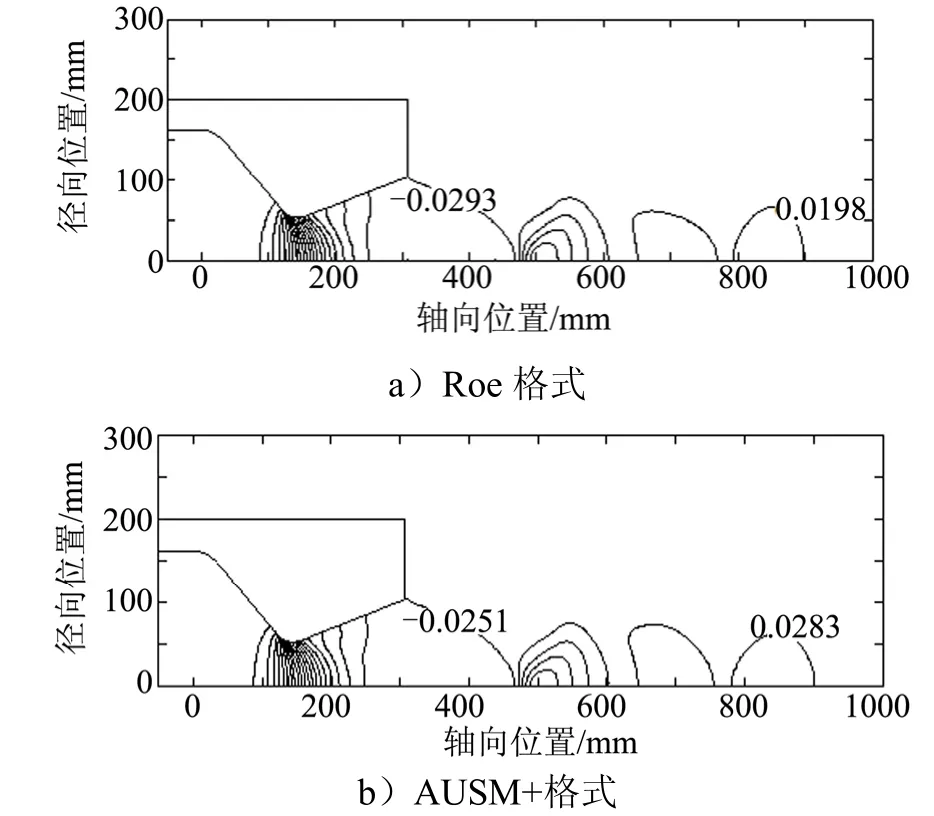
图13 自由喷流对称面静压分布等值线Fig.13 Contours of Static Pressure at the Symmetry Plane of the Free Jet Flow Field

自由喷流是经典的燃气流场算例，燃气由喷管射出后，交替出现收缩扩张现象，呈葫芦状分布规律。由图13和图14可见，Roe格式与AUSM+格式计算结果充分反映了自由喷流的流动特性，且两者表现出了高度一致性。主要区别在于AUSM+格式所得马赫数云图在燃气流边缘等值线存在波动，这同样是其标量形式的数值耗散所造成的，结合之前喷管内流场计算结果，可见AUSM+格式具有流动边界处易产生数值波动的特点。

5 结 论

a）开发了基于Roe格式、AUSM+格式和NND格式的燃气流场计算程序，3种格式在各算例中模拟结果基本一致，表现了良好的数值稳定性和激波捕捉能力。前台阶激波反射流场计算结果与文献结果相符，验证了程序计算结果的可靠性。

b）在喷管内流场算例中，由于AUSM+格式在壁面附近垂直壁面方向耗散项数值几乎为零，导致计算结果在壁面附近产生数值振荡，由于类似原因，在自由喷流算例中，其计算结果在燃气流边缘也产生了波动。

c）在喷管内流场算例中，由于NND格式对正负流通量的处理分别采用迎风差分和中心差分，其受下游数据的影响高于另两种迎风格式，导致计算结果在出口附近产生波动。

d）由于数值耗散不同，3种格式计算结果在喷管径向数值变化幅度上存在差异，AUSM+格式变化幅度最大，NND格式变化幅度最小。