液体火箭发动机试验台健康评估与故障预测方法

陈文丽，周 磊，刘瑞敏

（北京航天试验技术研究所，北京，100074）

0 引 言

液体火箭发动机试验台健康评估与故障预测是确定试验台当前状态偏离正常态的程度（故障级别）以及预测试验台后续的健康性能。在液体火箭发动机试验台上实施健康评估和故障预测，对指导试验技术人员实施规划维修[1]具有重要意义。当前，大多数文献都是对液体火箭发动机试验台进行故障诊断研究[2～5]，也有一些针对机械设备进行性能预测方面的研究[6～8]，但是针对液体火箭发动机试验台的健康评估和故障预测研究甚少。

模糊综合评判是一种基于模糊数学的综合评判方法，其根据隶属度理论对受多种因素制约的对象做出一个总体的定量评价，可解决模糊的、难以量化的计算问题。自适应相关向量机（Adaptive Relevance Vector Machine，ARVM）是一种基于贝叶斯概率学习模型的有监督小样本学习理论，其在贝叶斯框架下，利用自相关判定理论移除不相关的数据点，获得稀疏化的模型[4～7]。它能够克服神经网络故障预测需要较多训练样本的缺陷，也能够克服支持向量机故障预测核函数必须满足Mercer条件[8,9]的限制。

本文在研究液体火箭发动机地面试验参数特征的基础之上，提出将模糊综合评判理论和自适应相关向量机理论相结合，建立液体火箭发动机试验台健康评估和故障预测体系模型。计算结果表明，该方法能够对试验台健康状况进行定量的、合理的评价和预测，对试验系统指导实施故障前维修具有参考价值，该方法也可扩展应用于其他复杂系统的健康评估和故障预测中。

1 健康评估方法

1.1 健康度的定义

健康度hd是对试验台健康状况的定量度量。由于液体火箭发动机试验台系统复杂，测量参数众多，分为很多子系统，因此影响各个部分正常运行的因素也是多样的，如温度、湿度、电压波动等。为了全面、准确地反映试验台各个测点、子系统和试验台的整体健康状况，定义了单参数健康度、子系统健康度和试验台综合健康度。设试验台分为k个子系统，第j个子系统有m个测量参数，且第i个测量参数在发动机点火各时刻的值为 Xi=( xi1,xi2,…, xin)，则单参数健康度可表示为

1.2 模糊综合评判的数学模型

模糊综合评判是模糊集合理论在风险评价中的具体应用，是利用模糊变换原理，考虑与被评价对象相关的各个因素后，作出综合的评价，其数学模型如下：

a）建立因素集。

根据所研究的对象，确定影响对象的因素，组成普通因素集，即：

式中 vi(i = 1 ,2,…, m )为影响评价对象的第i个因素。

b）确定权重集。

因为普通因素集中各个因素对评价对象的影响程度是不同的，为了反映各个因素对评价对象的影响，为因素 vi分配一个相应的权值 αi(i= 1 ,2,…,m)，形成权重集，即：

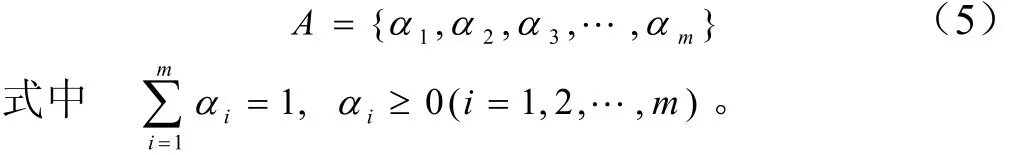
c）确定评价集。

评价集是对评价对象做出的各种评价结果组成的集合，即：

式中 uj为第j个评判结果。

单因素模糊评判是单独从一个因素 vi出发进行的评判，目的是确定评价对象对评价集元素uj( j = 1 ,2,… ,n )的隶属程度 rij。对第i个元素评价结果的单因素模糊评价集为

以各个单因素模糊评价集的隶属度为行向量构成单因素模糊评价矩阵，即：

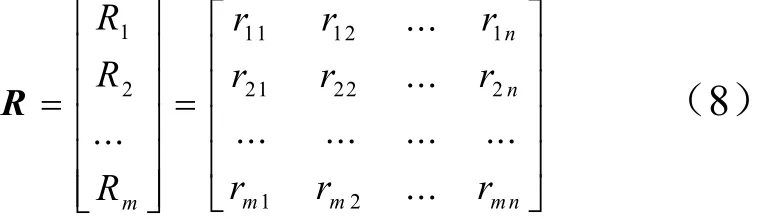
显然单因素模糊综合评判仅仅反映了一个因素对评价结果的影响，不能反映所有因素的综合影响，因而并不能准确反映评价结果。为得出客观、正确的评价结果，综合考虑所有因素的影响，形成对研究对象的综合评价。应综合评价集B由权重集A与单因素模糊评价矩阵R合成得到，即：

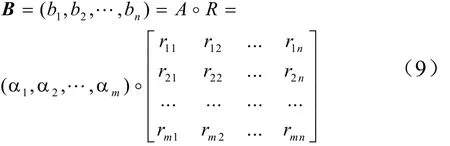
根据权重集A与综合评价集R的合成求取综合评价集B，有如下3种模型。

模型一：考虑评价的主要因素，采用算子对M(∧,∨)，其中∧为取小（min）运算；∨为取大（max）运算，则：

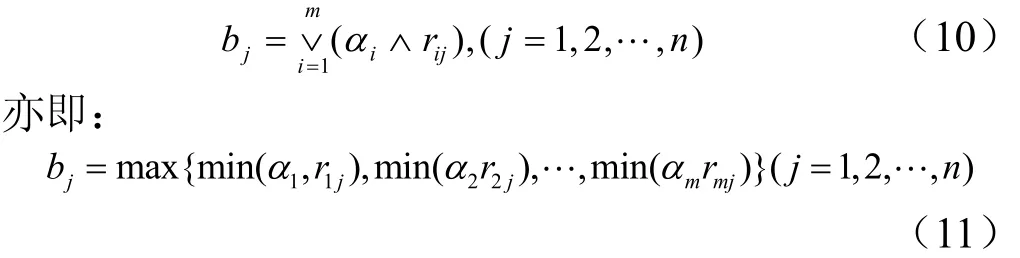
模型二：采用算子对 M (•,∧)，其中•为普通实数乘法运算，∧为取小（min）运算，则：

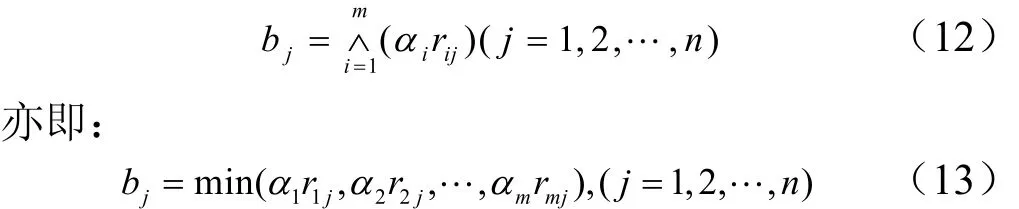
模型三：认为每个评价因素对综合评判结果都有贡献，采用算子对 M (•,+)，其中•为普通实数乘法运算，+为求和运算，则，

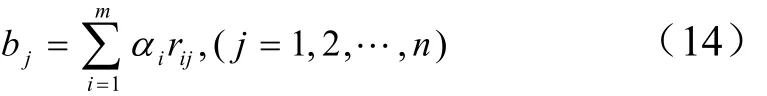
该类模型不仅考虑了所有评价因素的影响，而且还保留了单因素的评判信息。

1.3 健康度计算

在试验台运行的开始阶段，认为各个时刻点的参数对系统运行的重要程度是相同的。随着时间推移，参数会发生相应的变化，对系统性能的影响也会改变，因此在初始融合时，采用如下模糊综合评判的3种简化模型：

a）对于 M (∧,∨ ) ，令 rij（j=1,2,…,n)中最大值 rxj对应的权值 αx=1，其余的权值为0，得到第1种模型的评判指标：

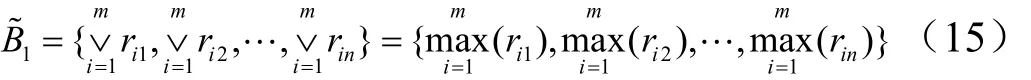
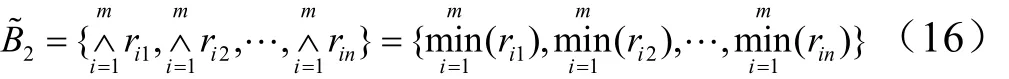
c）对于 M (•,+)，令 α1= α2=…=αm= 1/m，得到第3种模型的评判指标：

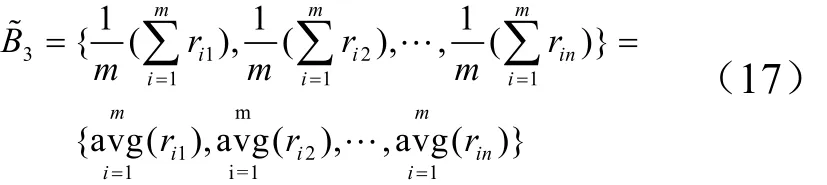
指标1B~是从最突出的优点考虑问题，指标2B~是从最突出的缺点考虑问题，指标3B~是从平均角度考虑问题。在实际应用中，如果仅取最大值、最小值或者平均值之一作为评判指标，具有片面性，因此可综合使用这3个指标，进行二级评判，得到二级综合评判矩阵R~。

表1 重要程度系数表Tab.1 Coefficients of Importance

隶属度函数完成了从精确的测量值到模糊量-隶属度的模糊化过程，而由隶属度计算健康度则实现了从模糊量-隶属度到精确量-健康度的去模糊化过程。由隶属度计算健康度的公式为

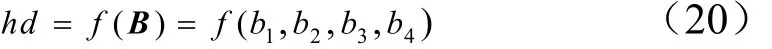
式中 B为经过模糊综合评判后得到的对于健康、亚健康、故障边缘和故障模糊集的隶属度。在实际计算中，根据试验台的具体情况采用下式的计算方式：

2 预测模型构建

给定训练集 { xn, tnn∈ Rd,tn∈ R ，同时假设所有输出变量ti全部由带有噪声的εi的模型产生。

式中 w为权值向量， w = [w1,w2, …, wi](i = 1,2,…, n )。

在液体火箭发动机试验中，受恶劣试验环境和各种物理因素的影响，试验现场测得的数据中通常会包含一些波动较大的数据点[1]，这些数据点可看作是正常的试验数据中夹杂了不规则的噪声所致，因而实际的试验数据集的噪声分布不能单纯地假设为服从同方差的高斯分布。设训练数据集中第i个样本的噪声εi服从的密度分布为

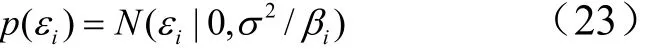
式中 σ2为所有样本的平均方差；βi为引入的噪声方差系数，并且假设其先验分布满足γ分布，即 p ( βi) = γ( ai, bi)。定义噪声方差系数向量 β =[β1, β2,…,βN]T，则训练样本的似然函数 p (t|w,β,σ2) 可表示为

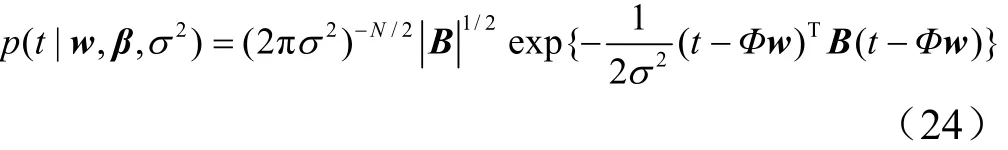
2.1 ARVM预测数学模型[9]

式中B为矩阵的行列式， B =diag(β1,β2,… ,βN) ，依据贝叶斯定理得到权值向量w的后验分布为

由于w后验分布均值µ和协方差矩阵Σ中含有超参数 α ,σ2以及噪声方差系数向量β，需要对其进行优化。根据相关向量机学习理论以及贝叶斯证据过程，超参数和噪声方差系数的优化通过最大化边缘似然函数p(t|α,β,σ2) 和 β 的先验分布 p (β)的乘积来实现。由前文假设可知，βi的先验分布为γ分布，即：

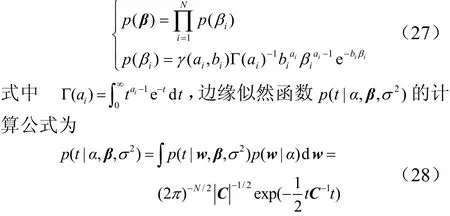
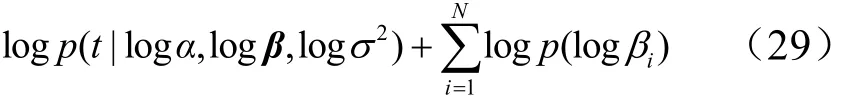
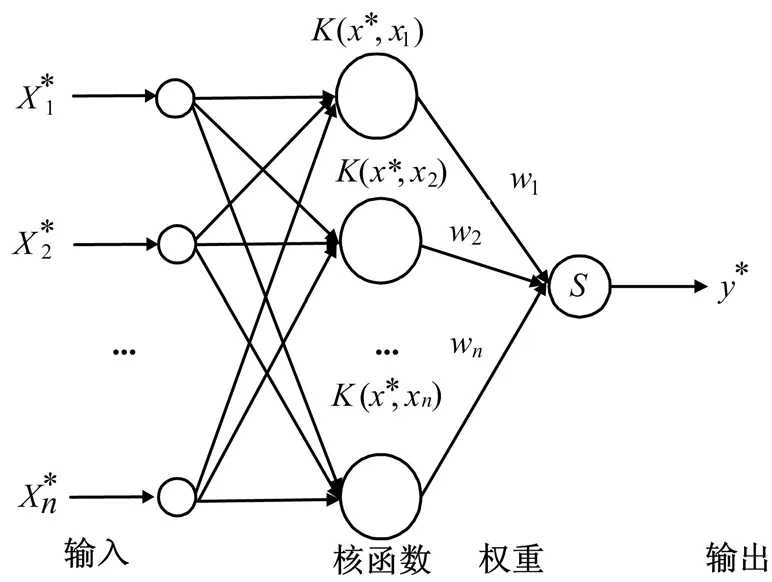
图1 ARVM回归预测模型结构Fig.1 Structure of ARVM Prediction

2.2 ARVM模型超参数优化[10]

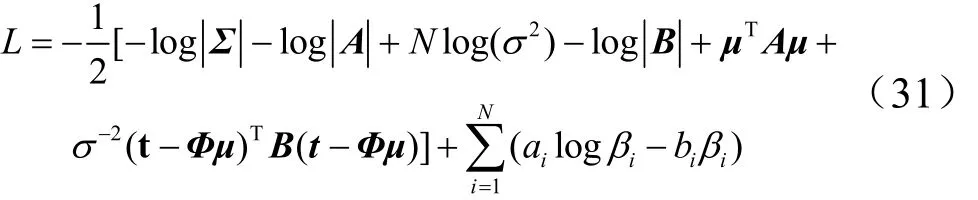
分别对logβi，logαj和logσ2求偏导，并令导数式等于0即可得到超参数α,β和σ2的迭代计算公式。

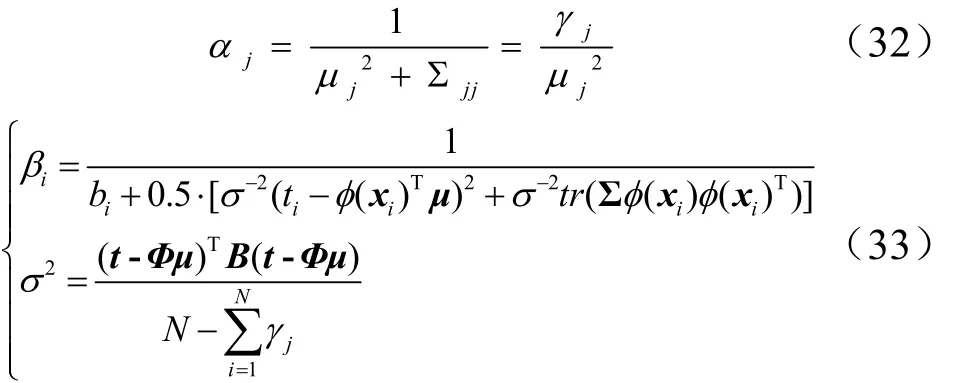
式中 µj为均值向量µ的第j个元素；Σjj为协方差矩阵 Σ 的第j个对角元，γj= 1-αjΣjj。ARVM算法流程如图2所示。

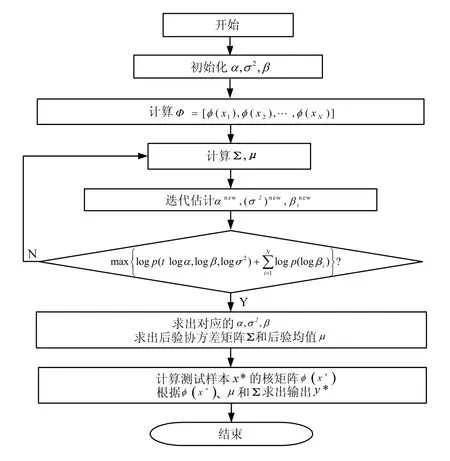
图2 ARVM计算流程Fig.2 Calculation Process of ARVM

3 测试分析

3.1 评价指标

引入MSEE 来评价模型的预测性能，其计算公式为

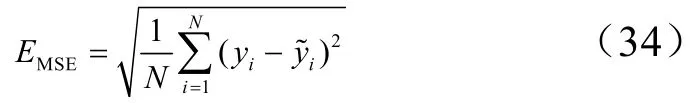
式中 N为数据点个数；iy为预测数据值；iy~为实际数据值。

3.2 时间序列的相空间重构

液体火箭发动机试验台健康度是表征试验台健康状况的定量指标，是多参数多变量相互融合的结果。由于试验台在运行过程中受多种因素的影响，导致基于时间的健康度值之间存在很强的非线性。那么在进行试验台健康状况预测之前，首要的是挖掘出非线性健康度序列中存在的关联关系，找出健康度值中隐藏的试验台故障演化规律，从而使一维时间健康度序列能够纳入ARVM预测模型的应用框架内。相空间重构法为挖掘一维时间序列的试验台健康度值中隐藏的关联信息提供了一条途径，其基本方法是将一维的时间序列进行反向迭代以构造出原系统的相空间，具体为：对于给定的原始健康度序列 X = { x1,x2,… ,xn}，将时间序列中的元素进行样本重排，设嵌入维数为 m，则通过相空间重构后的数据矩阵如表2所示。

表2 相重构数据矩阵Tab.2 Matrix of Phase Reconstruction

通过上述方法可构造出预测模型的输入和输出样本，即建立起映射f： Rm→ Rm+1，满足：

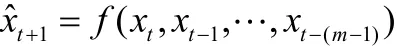
3.3 时间序列健康度预测

用本文提出的方法对某型液体火箭发动机试验台燃料增压系统进行健康状况评估和故障预测。数据来源于某次试验50 s点火程序稳态阶段的试验数据，通过模糊综合评判方法计算得到燃料增压系统健康度，曲线如图3所示。通过间隔计算获得了40组健康度值构成数据序列 X = { x1,x2, …, x50}。对数据序列进行相空间重构，获得了数据间的关联关系，形成ARVM预测模型的输入输出训练样本数据矩阵 Xtrain和 Ytrain，训练样本25组，测试样本15组，相空间重构嵌入维数m=3。

根据重构后的训练样本阵列进行ARVM预测模型的训练，并采用一步迭代预测法预测试验台未来15个时刻点的健康度值。根据离散数据特点，核函数选取为线性样条函数Spline，如式（36）所示。

通过网格搜索法得到当核参数σ=1时，ARVM 模型的预测效果最优。根据相空间重构后的ARVM预测模型得到的试验台稳态阶段燃料增压系统健康度发展趋势如图 4所示，训练样本和测试样本的预测误差如图5和表3所示。

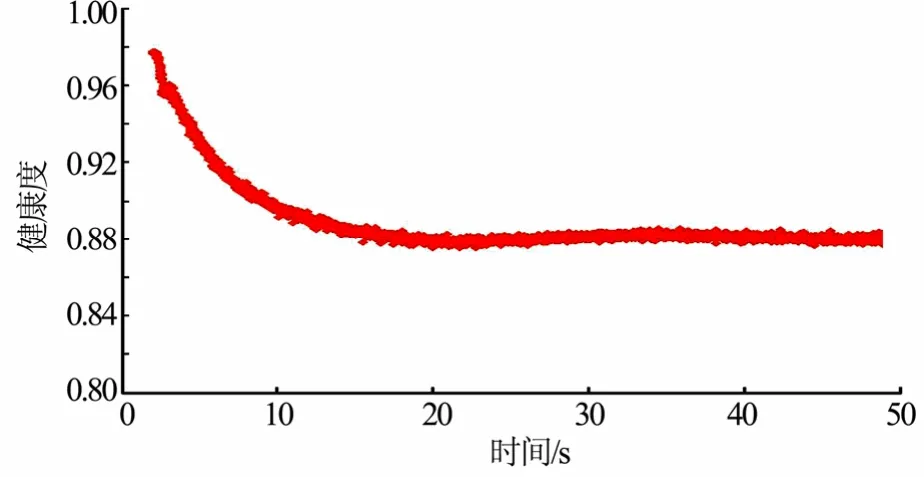
图3 燃料增压系统健康度曲线Fig.3 Health Degree Curve of Fuel Booste System

由图3可知，从点火开始至点火结束，试验台稳态工作段燃料增压系统健康度有缓慢下降的趋势，说明在发动机点火过程中测得的试验数据中有逐渐恶化的迹象，产生此种现象的原因是随着点火的进行，测量燃料入口压力Pif的传感器受发动机热辐射的影响发生了温漂。

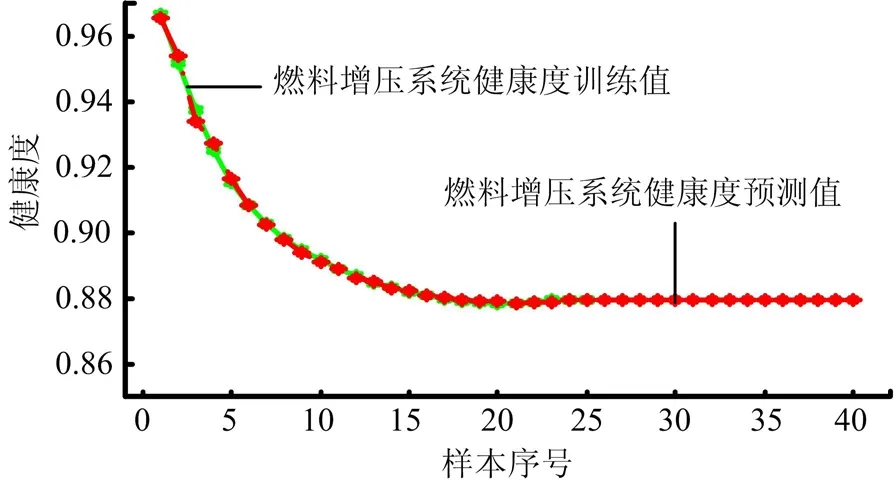
图4 ARVM健康度预测曲线Fig.4 Health Degree Prediction Curve with ARVM

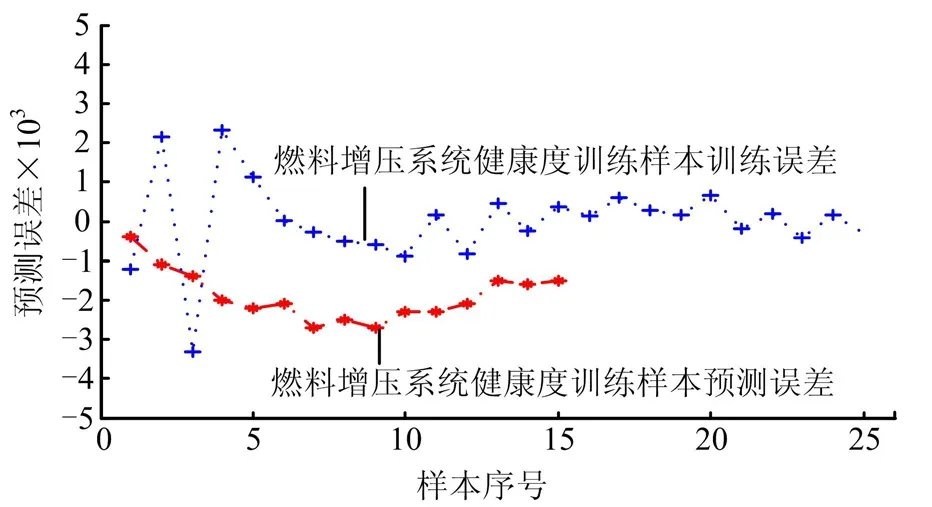
图5 基于ARVM算法的健康度预测误差曲线Fig.5 Error Curve of Health Degree Prediction Based on ARVM

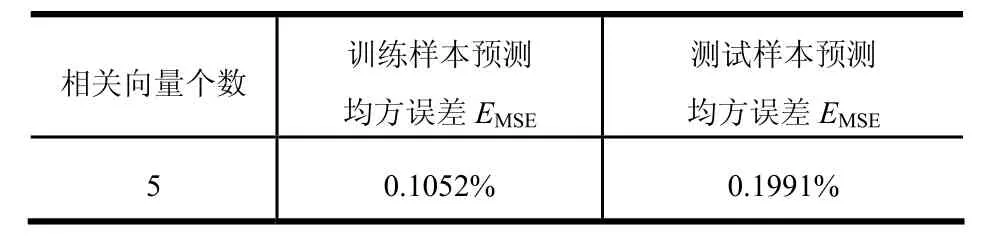
表3 预测效果分析Tab.3 Analysis of Prediction Result

由图4、图5和表3可知，ARVM模型输出的健康度预测结果符合试验台健康度的发展趋势。在模型稀疏性方面，仅使用了5个相关向量;在预测精度方面，训练样本预测的均方误差为 0.1052%，测试样本预测的均方误差为0.1991%，预测精度较高。

4 结束语

本文针对液体火箭发动机试验台健康状况退化的问题，研究并给出了基于模糊综合评判和ARVM的健康评估与故障预测方法，并将其应用于某型轨控发动机燃料增压系统的健康度计算和预测仿真中。研究结果表明，本文提出的方法能够对试验台的健康状况给出定量的、合理的评价，并且对试验台的健康发展趋势给出精度较高的预测结果，从而为技术人员对试验台实施规划维修提供了有利依据。