基于近邻元分析算法的滚动轴承复合故障诊断

余 震

(黄河科技学院 医学院,郑州 450063)

作为旋转机械的关键支撑部件——滚动轴承,其安全高效运行及研究其有效的故障诊断方法具有重要的意义.当滚动轴承发生单一故障时,包络解调分析方法及新的旋转机械信号处理方法如谱峭度[1]、品质因子可调小波变换[2]等能有效提取出相应的故障特征频率.但当滚动轴承发生复合故障时,由于故障之间的相互耦合效应,包络解调分析方法及常规信号处理方法往往难以对其进行有效的特征提取.滚动轴承的复合故障智能诊断是一种有效的方法.文献[3]提出一种基于隐马尔科夫模型的卷积神经网络算法,并将其用于滚动轴承的智能故障诊断,取得了理想的诊断结果.文献[4]提出一种集成深度自动编码的智能算法,将其用于滚动轴承的故障分类、故障严重程度及故障发展趋势.文献[5]建立一种滚动轴承动态仿真模型,利用仿真模型数据来训练智能算法模型,解决了现有滚动轴承智能诊断算法依赖于设备历史运行数据的缺点.文献[6]将极限学习算法、静态小波变换以及奇异值分解方法相结合,用于滚动轴承故障的智能诊断,取得了理想分类效果.虽然基于智能诊断算法的滚动轴承故障诊断方法取得了相当的成绩,但上述算法大多存在实时性差或只针对滚动轴承单一故障有效的弊端.针对此问题,本文提出一种基于近邻元分析(Neighborhood Component Analysis,NCA)方法的滚动轴承智能诊断方法.虽然NCA方法在其他领域，如语言识别[7]、图像识别[8]等领域取得了相当的应用,但其在旋转机械故障诊断尤其是滚动轴承的复合故障诊断中还鲜有研究.

1 NCA

假设D维空间中分布有N个输入样本{x1,x2,…,xN},样本相应的类标签{c1,c2,…,cN},则样本点间的马氏距离为

(1)

式中:A为d×D维矩阵;ATA为马氏距离变换矩阵.

NCA中变换矩阵A的获取是通过优化留一法交叉检验,并通过优化留一法优化NCA分类结果.在优化过程中,通过约简维数以减少计算复杂度.

任意两样本xi与xj之间的类标签概率定义为

(2)

样本xi被正确分类的概率为

(3)

式中:Ci={j|cj=ci}.

如下NCA最大化式所示的目标函数在约简维数的同时,保证分类正确率为

(4)

式(4)满足如下关系式:

(5)

式中:xij=xi-xj.

NCA大致算法流程如下:

步骤1对变换矩阵A进行初始化;

步骤2利用式(2)和式(3)分别计算pij,pi;

步骤3利用式(5)对矩阵A进行更新.

在更新过程中当∂f(A)小于设置阈值时，停止迭代;否则重复步骤2及步骤3,直至满足迭代终止条件.

由上述NCA计算过程可知,相对于支持向量机、支持向量数据描述及隐马尔科夫等智能算法,NCA具有算法原理更加简单、实现效率更高的优点.

2 所述方法流程

基于NCA的滚动轴承复合故障诊断流程(见图1)如下:① 利用电火花技术分别加工滚动内圈、外圈、滚动体及保持架上点蚀故障;② 组合不同的滚动轴承复合故障(内圈、外圈复合故障，外圈滚动体复合故障以及内圈、外圈滚动体复合故障),并分别采取不同不和故障状态下的振动信号;③ 取部分振动信号作为测试样本训练NCA模型,对振动信号进行多源特征提取组成NCA输入训练向量,其中多源特征提取指标及相应的计算公式如表1所示;④ 取部分振动信号作为测试样本,同样对测试样本用表1所示的指标进行特征提取组成测试特征向量,具体步骤如图1所示.

图1 基于NCA的滚动轴承复合故障诊断流程Fig.1 The flowchart of diagnosis of bearing compound fault based on NCA表1 多源特征指标及计算公式Tab.1 The multi-source feature indexes with their calculation equations

序号时域特征计算公式1峰值x^=max{x(1),x(2),…,x(N)}2峰-峰值xp-p=max(|x(n)|)-min(|x(n)|)3平均幅值x—p=1N∑Nn=1x(n)4方根幅值xr=1N∑Nn=1x(n) 25有效值xRMS=1N∑Nn=1x2(n)6波形指标SF=有效值平均幅值=x^xr=1N∑Nn=1x2(n)1N∑Nn=1|x(n)|7脉冲指标IF=峰值平均幅值=x^x—p=max|x(n)|1N∑nn=1|x(n)|8峰值指标CF=峰值有效值=x^xRMS=max|x(n)|1N∑Nn=1x2(n)9裕度指标CLF=峰值方根幅值=x^xr=max|x(n)|1N∑Nn=1|x(n)| 210歪度指标SK=1N∑Nn=1x(n)-均值σ 3=1N∑Nn=1x(n)-x—σ 311峭度指标KU=1N∑Nn=1x(n)-均值σ 4=1N∑Nn=1x(n)-x—σ 4

3 实验

滚动轴承试验台如图2所示.滚动轴承类型及相关参数如表2所示.滚动轴承外圈、内圈及滚动体上所加工的故障如图3所示.根据表2相关参数及式(6)～式(8)滚动轴承故障特征频率计算公式得到试件的外圈、内圈及滚动体故障特征频率分别为fo=64.41 Hz,fi=95.38 Hz,fb=5.38 Hz.

式中：fr为转频.

图2 实验台实景图Fig.2 The test rig

表2 试件轴承相关参数Tab.2 The type and parameters of the test bearing

图3 试件故障Fig.3 The machined fault on bearing

滚动轴承4种运行状态(正常,外圈滚动体复合故障,外圈、内圈滚动体复合故障以及内圈、外圈复合故障)的时域波形图分别如图4(a)～图4(d)所示.用图1所示流程图分别对4种运行状态的时域数据进行处理,最终得到的NCA分类效果如图5所示.图5中,NC代表正常状态样本,ORF代表外圈滚动体复合故障样本,REF代表外圈内圈滚动体复合故障样本,IRF代表内圈外圈复合故障样本.由图5可以看出,利用所述方法对滚动正常的4种运行状态进行了正确的分类.

为突出所述方法的优越性,图6所示为主成分分析(Principle Component Analysis,PCA)方法对4种运行状态的分类结果,相对NCA方法存在着较高的误分率,说明了所述方法的优越性.

图4 滚动正常4种状态的时域波形图Fig.4 The time-domain waveforms of bearing’ four states

图5 基于NCA的滚动轴承复合故障诊断的分类结果Fig.5 The classification result of the bearing compound fault based on NCA

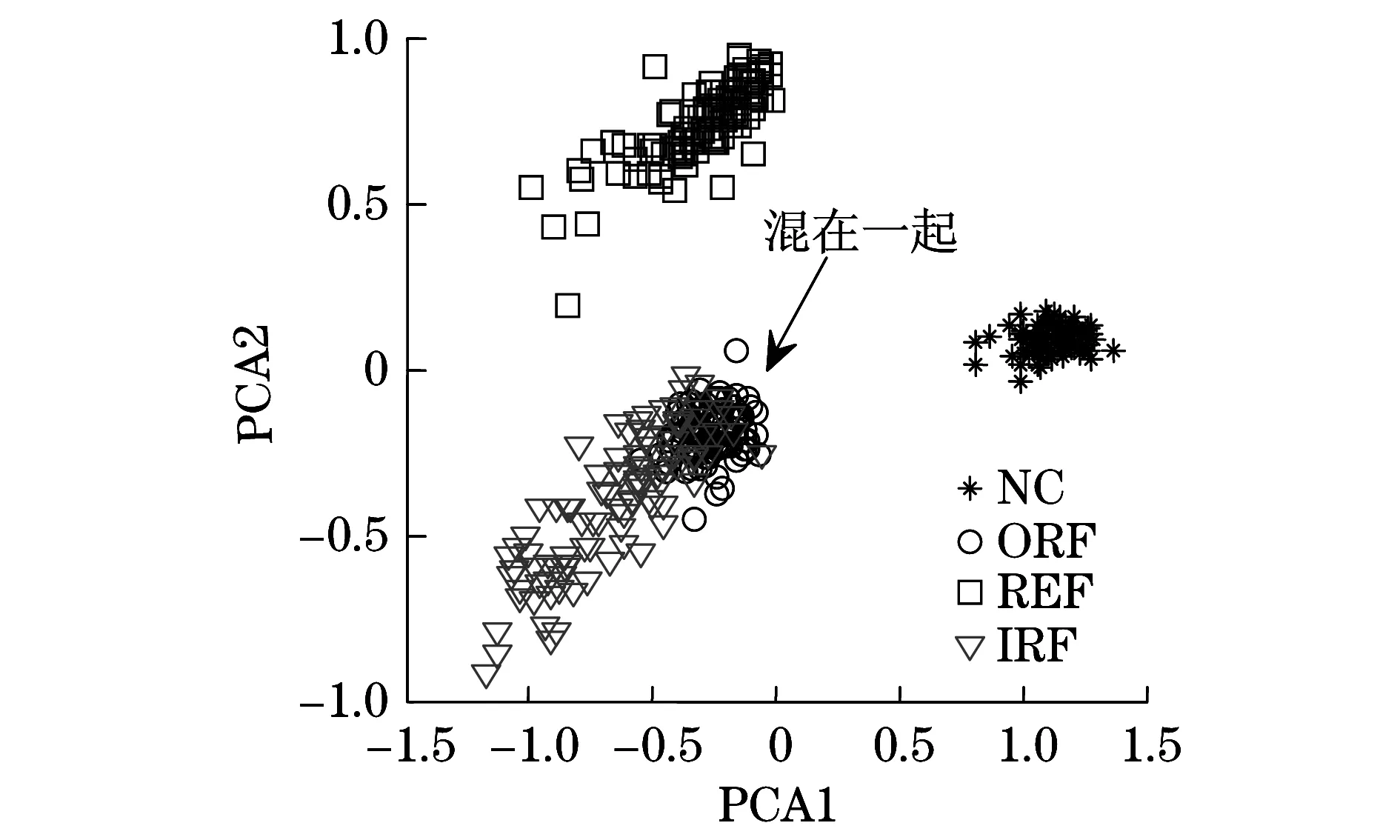
图6 基于PCA的分类结果Fig.6 The classification result by using PCA

4 结论

针对基于信号处理的滚动轴承复合故障诊断难的问题,提出一种基于NCA的滚动轴承复合故障智能诊断方法.为提高NCA的分类正确率及效率,用常规时域特征提取方法,对滚动轴承不同运行状态的信号进行特征提取,将提取后的特征向量作为NCA的训练及测试样本,取得理想的分类效果.通过滚动轴承3种复合故障振动数据及正常状态数据,验证了所述方法的有效性.此外,通过与PCA分类效果对比,证明了所述方法的优越性,具有更高的分类正确率.