基于0-1规划的五连珠问题求解

吴亚东，肖华勇



基于0-1规划的五连珠问题求解

吴亚东，肖华勇

（西北工业大学 理学院，陕西 西安 710129）

五连珠问题是五子棋中抽象出来的问题，通过建立0-1规划模型，求解得出一维、二维以及三维情况下五子连珠问题的可行解。类比晶体学中晶体的成核与生长过程，建立了晶胞构成模型。相比单纯的0-1规划模型，晶胞构成模型有运算规模小、运行速度快等优点。拓展至高维度情况下的连珠问题，讨论不同维数规划模型的约束类型的个数。该模型对于N子连珠问题以及八皇后的求解有一定的借鉴意义。

五子连珠；晶胞构成；0-1规划；N维约束

五子连珠问题是基于五子棋演变而来，规则为在一个棋盘中的每个小方格子的中心点各放一个棋子，如果两个棋子所在的小方格有公共边或公共顶点，那么则称这两个棋子相连。

针对五连珠问题的规则要求，我们建立了0-1规划模型，通过Lingo软件编程得到了在一维、二维以及三维空间下的可行解[1]。借鉴晶体学中晶体生长与晶胞构成，建立了晶胞构成模型求解连珠问题，讨论了在N维空间下的五子连珠问题的约束类型数目。

1 0-1规划模型建立

1.1 二维一般问题

以6×7的长方形棋盘为例，对前5列，每行至少需要去掉1个棋子，则前5列至少需要去掉6个棋子。对后两列，每列至少需要去掉1个棋子，因此后两列至少需要去掉2个棋子。则总的至少需要去掉8个棋子。如图1所示。

图2是一种去掉8个棋子而能满足条件的方式。

图1 6×7长方形棋盘

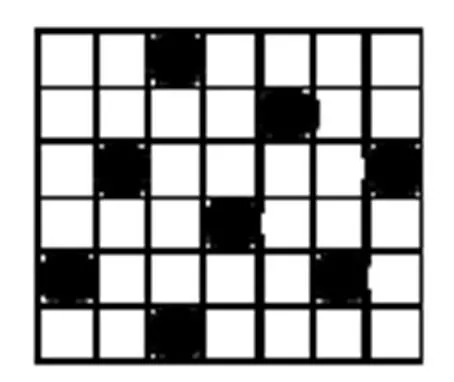
图2 6×7情况的一种解法

1.2 二维一般模型

对×的五连珠问题，建0-1决策变量[2-4]，设

去掉棋子数最少的目标函数设为：

每行连续5个格子中至少要去掉一个棋子，则有：

每列连续5个格子中至少要去掉一个棋子，则有：

每条反斜线上连续5个格子中至少要去掉一个棋子，则有：

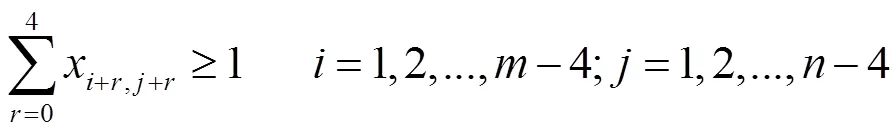
每条正斜线上连续5个格子中至少要去掉一个棋子，则有：

因此总的线性规划模型为：

约束总数：

当=13，=17时，=556，其约束条件如下：

13×17的棋盘需要44个棋子。

图3 13×17棋盘情况一种解法

1.3 三维一般模型

对××的五连珠问题，建0-1决策变量，设

去掉棋子数最少的目标函数为：

三个方向分别称为、及轴方向。

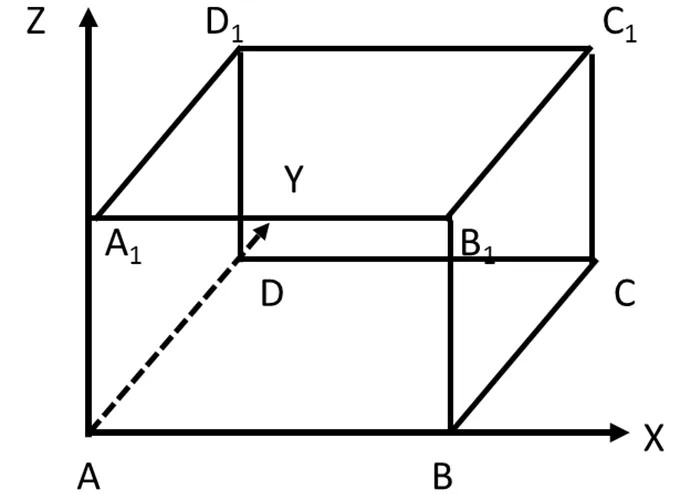
图4 4条空间对角线方向示意图

（1）只变一个方向的约束：

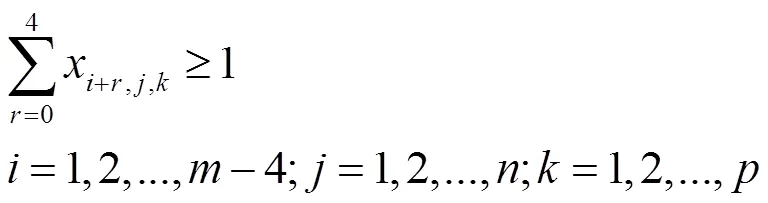
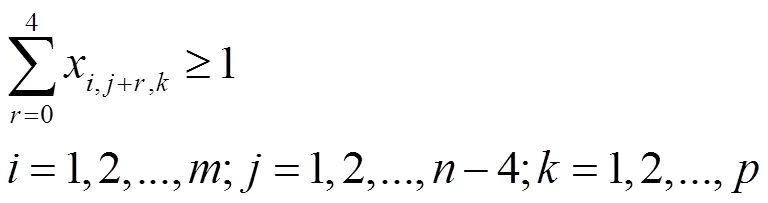
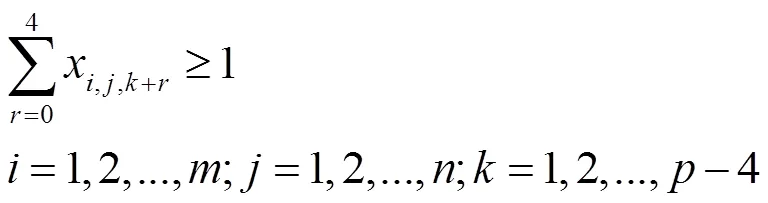
（2）变两个方向的约束：

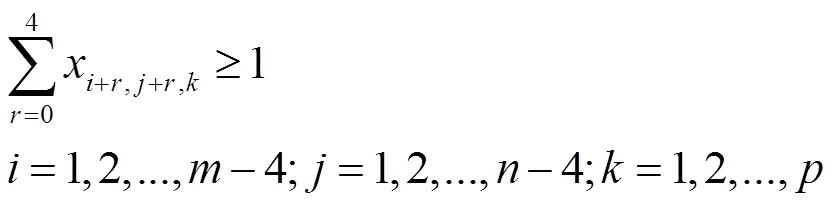
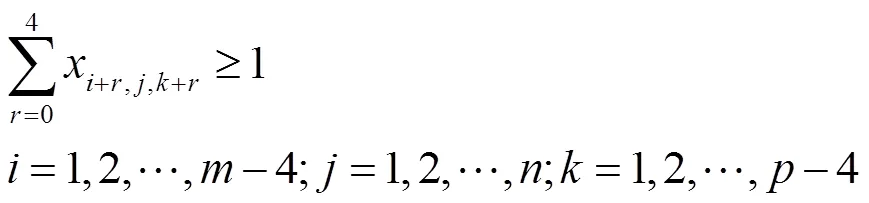
（3）变三个方向的约束

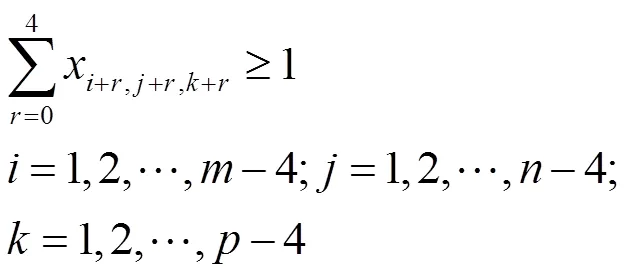
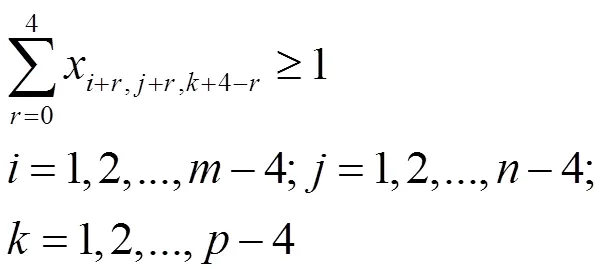
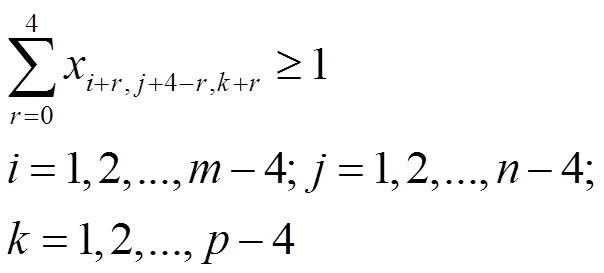
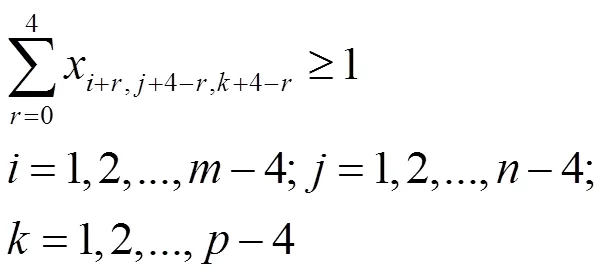
总共约束有3+6+4=13类。

约束总数：

线性规划模型为：

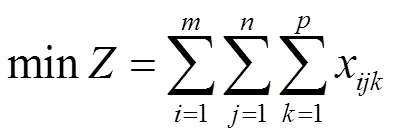
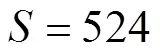
对于6×7×6棋盘，求解结果为64。

2 晶体生长模型建立

建立的0-1规划模型，可以求解小规模低维度的问题，但对于高维度大规模的棋盘，其求解速度有待提高。为此我们引入晶体学中晶胞的概念以简化问题。

晶胞：构成晶体的最基本的几何单元，是能完整反映晶体内部原子或离子在三维空间分布之化学结构特征的平行六面体最小单元[5]。

2.1 一维晶胞模型

当我们将二维问题降维到一维问题（以=13为例）时，其一般的结果如图5所示。

图5 一维一般问题

从图5可以发现，黑棋子总是每隔4个就出现一次，同理，5连续的5个棋子可以看做是一个循环单元，如果恰巧就是5的整数倍，那么只是循环单元在反复地、完整地出现，这与晶胞的概念类似。将连续的5个棋子视为“一维晶胞”，一维棋盘的增长、扩张就类似晶体由晶核生长为晶体的过程。可以将问题简化如下：首先求解出一个有效的晶胞，然后让其“生长”为边长是5的整数倍的棋盘，最后根据给定的棋盘大小从中统计出最少的棋子的排列方式。例如，对于边长为13的棋盘来讲，先求解边长为5棋盘，再将其平移复制2个成为边长为15的棋盘，统计连续13个格子中黑子的数目，即可找到最少黑子的边长为13的棋盘分布，此为一个可行解。避免了直接求解大规模棋盘就可以得到可行解，而且还可能得到多个可行解。

2.2 二维晶胞模型

二维13×17棋盘的一种解如图6所示。

可以发现类二维棋盘中的二维晶胞（图6中虚线内部分），其大小为5×5。求解二维晶胞的思路可以用图7-图9示意。

一张二维平面，将其上下连接在一起，左右也连接在一起，两个斜对角线也连接在一起，见图7。由平面变成圆筒，再变为圆环，见图8。在每一个点处的横向、纵向、斜向都满足五连珠条件，则可得到原平面的二维晶胞，见图9。

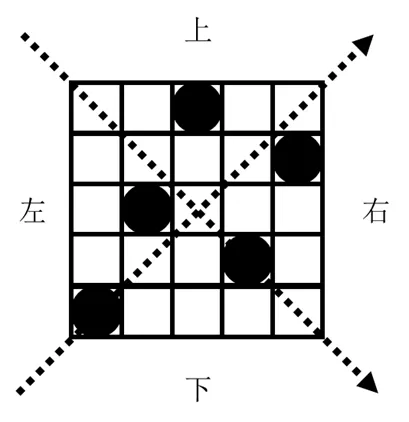
图7 有效晶胞的约束方式

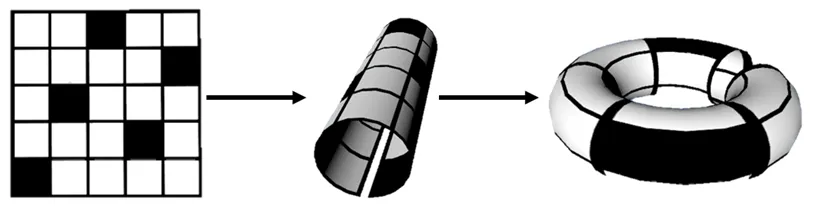
图8 二维有效晶胞约束示意图

图9 二维有效晶胞

有了二维晶胞以后，对其进行平移复制为20×25的二维棋盘，从中统计出以13、17为边长的长方形棋盘内最少的黑子数目（44个），得到图10中的2种完全不同的解，其中的一种在之前未求解出。若对其进行对称、旋转变换可得到更多的可行解。