这些高中内容该不该在初中补充？——以初中数学中考复习几个片段为例

江苏省无锡市港下中学 (邮编：214199)

1 问题的提出

在进行初中数学中考专题复习阶段，经常听到或看到这样的解法依据：

依据1 平面内“若直线L1⊥L2垂直，则斜率k1k2=-1(斜率存在的话)”；

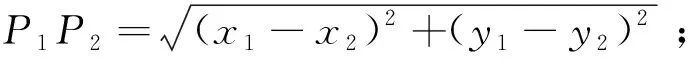
依据3 平面内点P(x0，y0)到已知直线L:Ax+By+C=0的距离为

显然，这是高中课程的内容，面对上述“咄咄逼人”的数学法则和依据，初中数学教师有时显得很难把握教学的度，比较困惑，现摘几例，以飨读者.

2 案例回放

2.1 片段一 求已知点关于已知直线的对称点——初高中解法“碰撞”

例1 已知，矩形ABCO两边与坐标轴重合，且B(1，2)，现将△ABC沿AC翻折，B的对称点为B′，则B′坐标为_________；

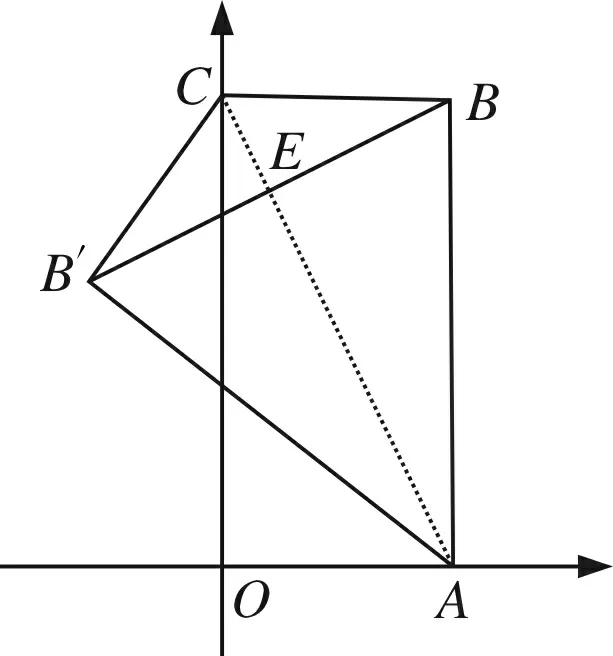
这是一道常见的中考复习题，学生常常觉得吃不消，教师感觉教学效果不理想，且往往找不到好的办法，引导学生功克难关.相关解法摘录如下：

解法一

步骤1 先用待定系数法求出直线AC的解析式为LAC：y=-2x+2；

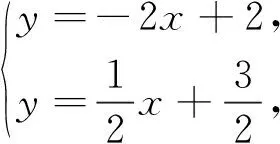
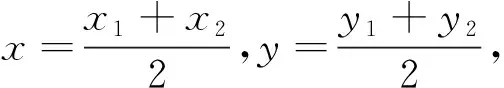
上述解法思路清晰，有高中解法的痕迹，但必须对初中学生补充两点

①平面内“若直线L1⊥L2垂直，则斜率k1k2=-1(斜率存在)”；②中点坐标公式；

解法二

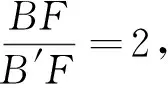
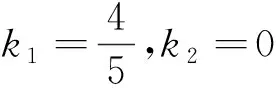
反思1 解法一忽略了初中数学求点坐标的基本方法，绕开了初中数学中的相似三角形和勾股定理这一主要运算工具.其中步骤1已涉及到高中解析几何内容，即k1k2=-1⟺L1⊥L2.初中数学课程中没有这样高的要求，是否拔高了？

反思2 解法二中求点的坐标是初中数学中考中的常见题型，通常做法是作垂线，法二中步骤1体现了这一基本理念.求点坐标最终转化为求线段长度，这是初中数学数形结合的重要体现.步骤1中构造相似三角形，步骤2中利用勾股定理就是集中体现.相似三角形和勾股定理是初中数学求线段长的主要手段，学生对此也十分熟悉.最后通过平移解决问题.涉及到初中数学常见的基本图形——“K”字形图；涉及到初中数学的核心运算工具——相似和勾股定理，涉及到求坐标的一般数学思想——数形结合思想.解法二是否具有普适性？能否体现这一类问题的基本解题思路和解题规律？现举例说明.

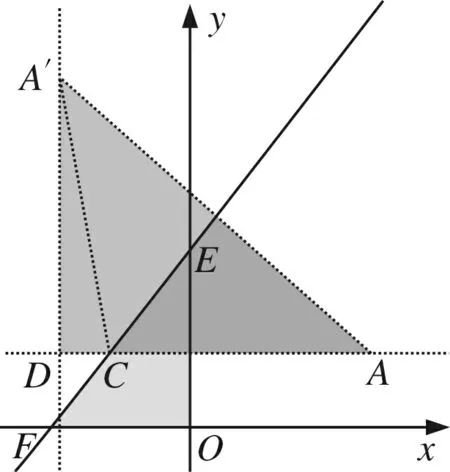
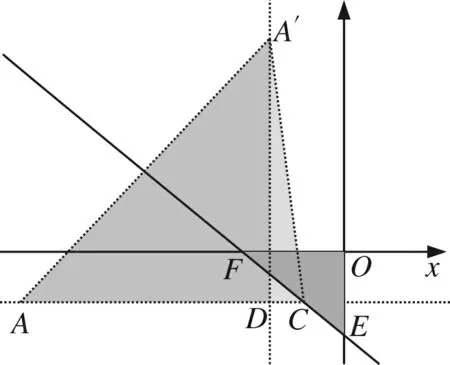
图3 图4

例2 已知，直线L：y=kx+c(k≠0)，求点A(a,b)关于直线L的对称点A′坐标.

解法回放如图A′和A关于直线L对称(如图3)

步骤2 由对称性知，CA=CA′，

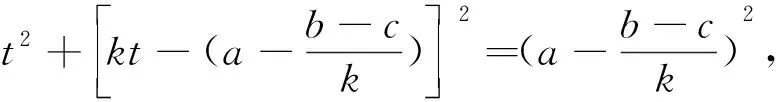
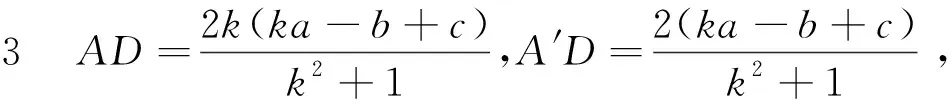
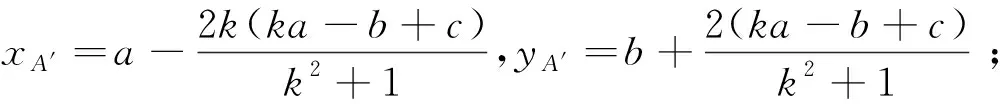
当k<0时，有类似的做法(如图4).

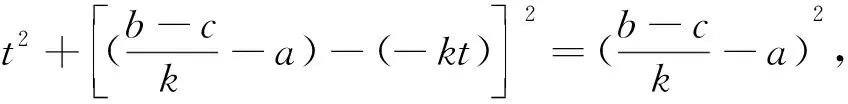
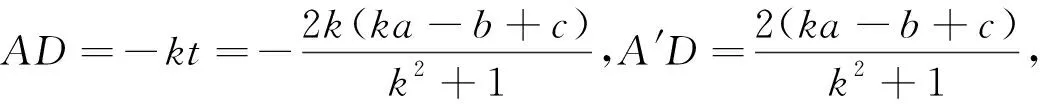
解后反思1 在上述解题过程中，构造Rt△A′AD与Rt△OEF相似是常用做法；在Rt△A′DC中利用勾股定理是初中学生的必然选择，结合轴对称性(CA=CA′),从而求出AD和A′D长，最终利用平移规律解决问题.

解后反思2 在上述解法中，有几点是学生必须掌握的技能，

(1)求点的坐标常常作垂线，

(2)构造Rt△找相似(往往用与已知直线与坐标轴围成的Rt△)

(3)利用勾股定理求线段长；

(4)利用平移求点坐标；

这些都涉及到初中数学的核心数学思想和方法，如数形结合思想，平移变换规律等.是学生能掌握且必须掌握的基本技能和思想方法.例1解法一不适合学生的胃口，可以避开.

2.2 片段二 初中阶段，两点距离公式有没有必要补充？

例3 如图A(1，5)，B(-2，-1),C(5，3)试说明△ABC为直角三角形.

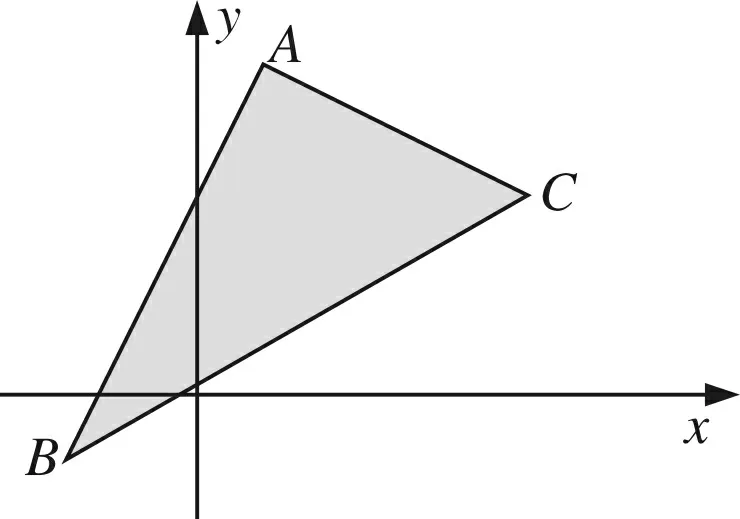
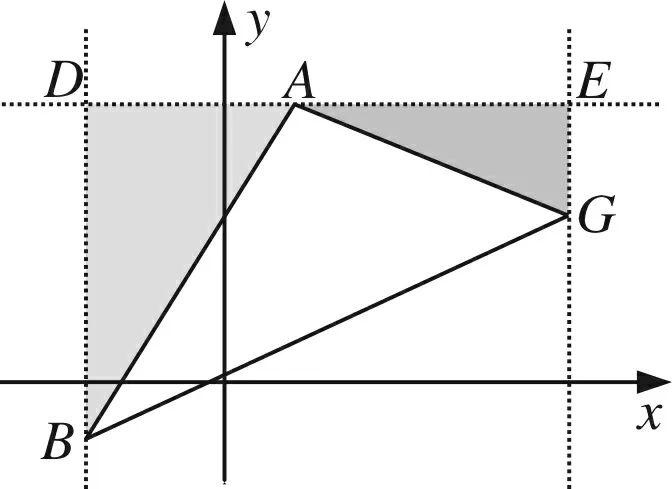
图5 图6

解法一预先给出平面内两点距离公式(或学生已经知道公式)，

步骤1 由距离公式，

步骤2AB2+AC2=BC2，利用勾股定理逆定理，∠BAC=90°.

解法二

步骤1 构造直角△(如图6)，产生“K”字形.

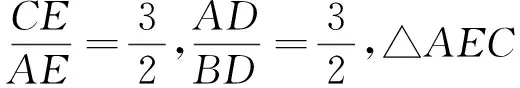
步骤3 得∠DBA=∠EAC，又∠DBA+∠DAB=90°，故∠BAC=90°.

解后反思1 解法一运用两点距离公式，实质也是运用勾股定理，学生解题的重心就是运算，很少关注图形本身，重“数”轻“形”.但解题思路十分清楚，效果不错，学生运用定理也不觉得陌生.不可否认，这里补充该距离公式有一定的合理性和现实意义.

解后反思2 解法二就是初中数学的基本解法，既有运算也有图形识别，用到几何知识，数形兼顾，适合学生“胃口”，也符合课程标准精神，是初中数学中考方向.从解题效果看法一和法二均可，但从学生教学要求和培养学生能力来看，似乎法二更恰当些.

2.3 片段3作为应试，用“点到直线距离公式”计算是否更快捷合算？

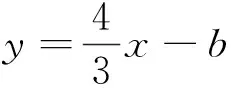
A.-2或4 B.2或-4

C.4或-6 D.-4或6

解法一

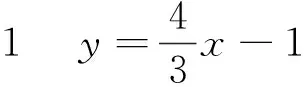
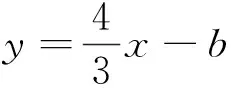
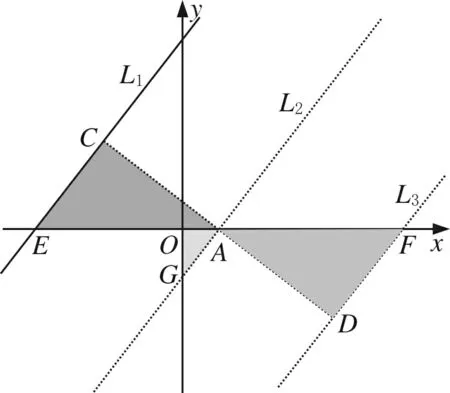
图7

解法二

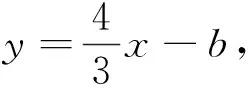
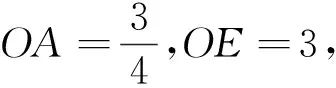
解后反思解法一显然用了高中解析几何中点到直线距离公式，绕开了相似工具，重“数”轻“形”，甚至可以不画草图轻松求得两解.作为选择题，既快捷又正确，非常划算.可能已经出乎命题者的意料，无法考查初中学生的数学解题能力，对没有学习到“点到直线距离公式”的学生来说，似乎不太公平.

解法二就很好地考查了学生的基本解题能力，构造相似△，考查了点到直线的距离概念，考查了分类思想，画图能力等等，但费时，易错.由于中考数学试题具有指挥棒的作用，一线教师到底该不该补充这一公式？值得深思！

3 几点教学思考

3.1 尊重初中数学课程标准，尊重初中数学基本教学要求

初中课程标准要求学生的形象思维与抽象思维并重，注重培养学生数形结合思想.相似与勾股定理是初中学生解决问题的重要工具.片段一中，解法二构造了直角三角形和相似三角形，用到了对称性质，完全符合中考考查要求，涉及到的基本知识和技能符合初中数学课程标准的精神.而解法一，则违背了初中课程标准的精神，超出了初中数学的基本要求.

3.2 尊重初中学生的认知能力，尊重数学知识的认识规律

初中学生的抽象思维能力尚不发达.数和形相结合呈现数学知识，最合适现阶段的学生.片段一中，解法二更适合初中学生现有的认知水平，学生对勾股定理和相似三角形十分熟悉，初中阶段有思维力度的题目主要围绕他们展开，如用高中知识解决，那么初中数学知识则完全被“架空”，也超出了学生的学习能力.片段三解法一用到点到直线距离公式，已超出了学生的认识水平，是应试教育的“不健康产物”.数学知识的掌握是“螺旋式”上升的，要循序渐进，逐步提升.

3.3 做好初高中教学的衔接工作，与时俱进，恰当对待高中知识

初高中数学知识并不矛盾，科学对待初中数学解题的局限性，合理处理初高中教学的冲突.片段二解法一学生普遍能接受，两点间距离公式虽是高中内容，但它是勾股定理的延伸，加以补充，便于学生计算长度，有一定现实意义.