三角形两个性质在四面体中的引申①

曾建国

(赣南师范大学数学与计算机科学学院 341000)

1 引言

文献[1]载有三角形的两个共线点定理(图1)：

性质1过一点O对直线OA，OB，OC作垂线，与△ABC的对边交于三个共线点(图1).

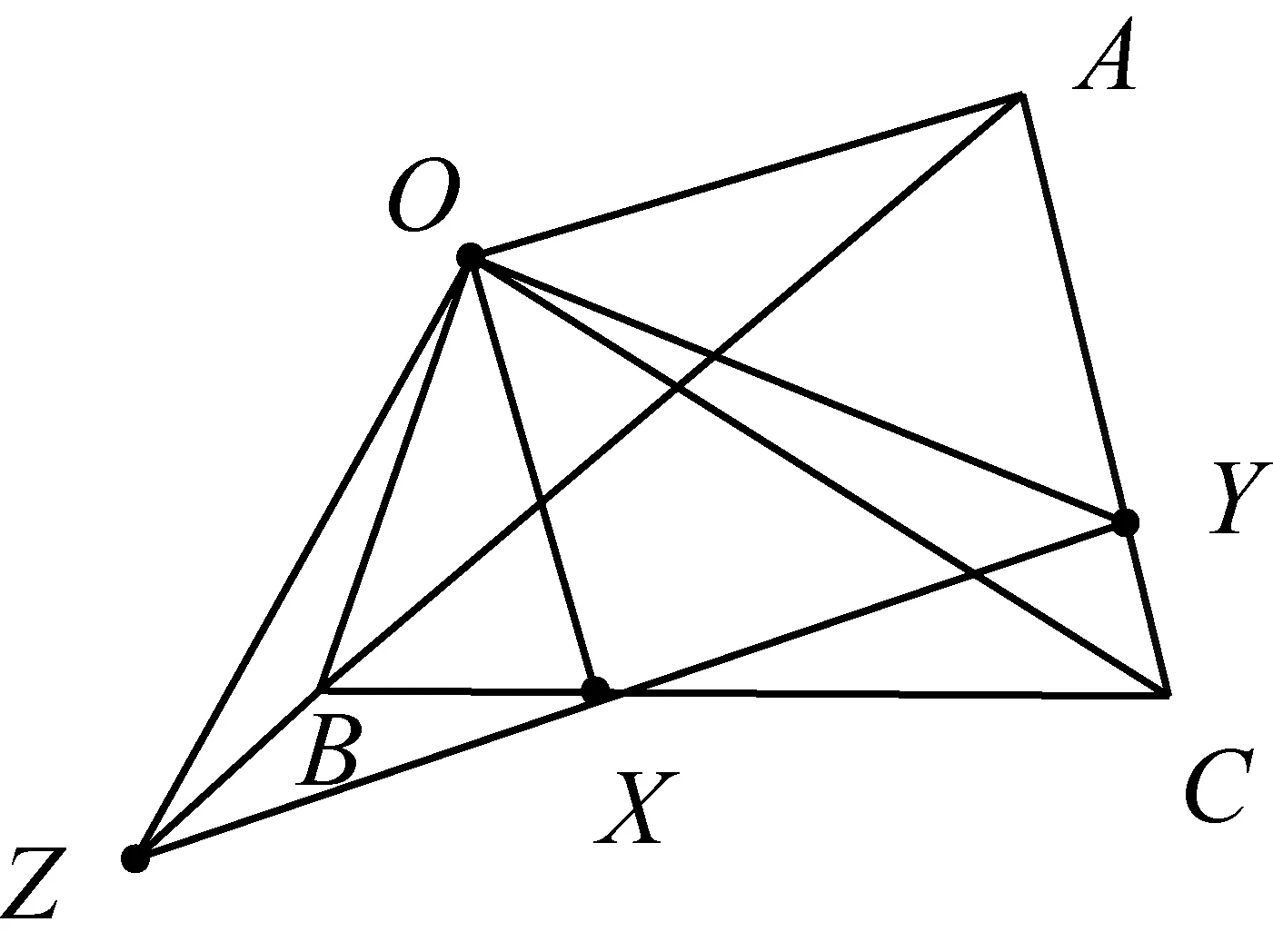
图1

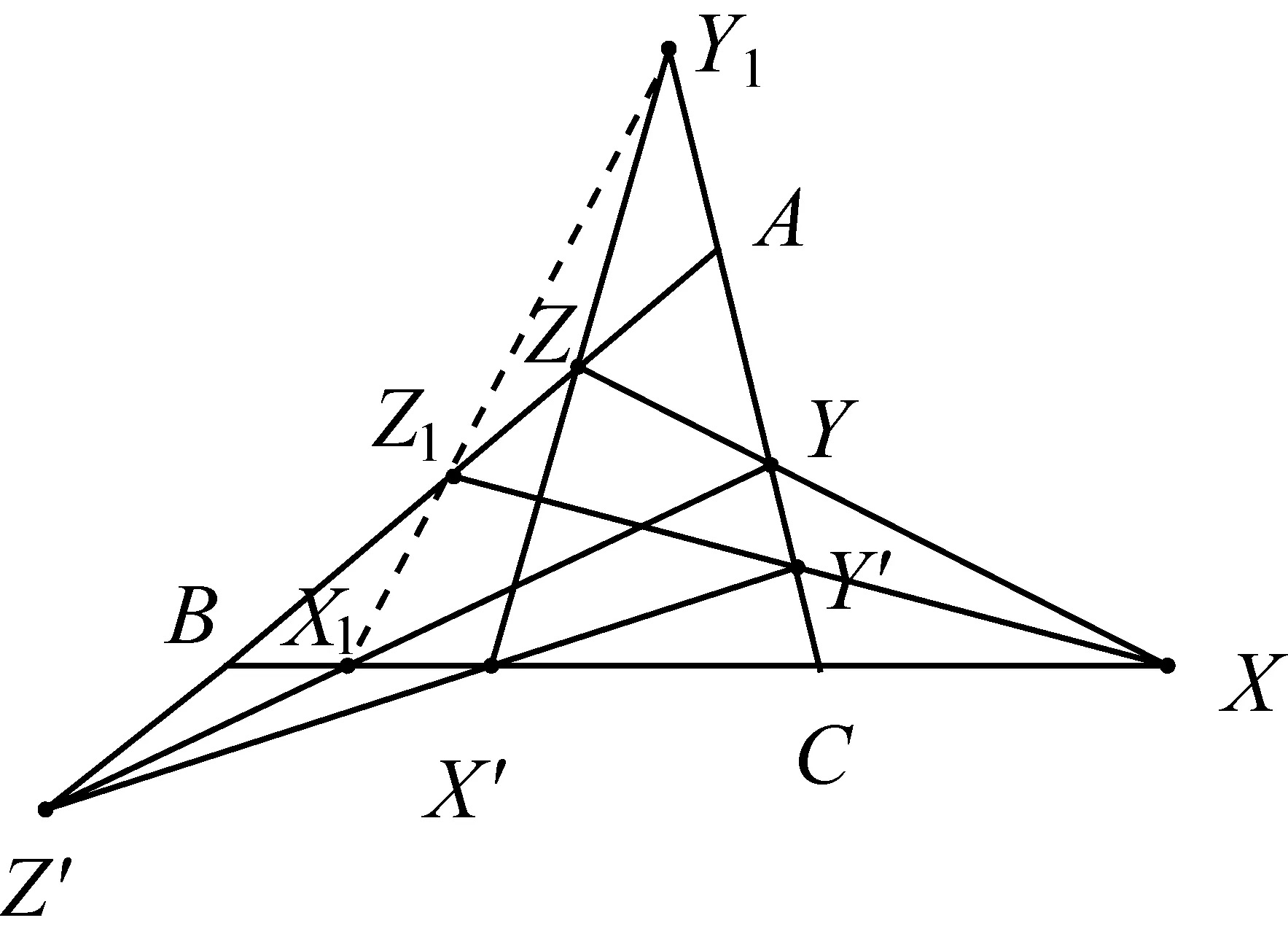
图2

性质2如果XYZ，X′Y′Z′是△ABC的任意两条截线，则直线YZ′，ZX′，XY′与BC，CA，AB交于三个共线点(即图2中X1,Y1,Z1共线).

本文将这两个性质引申至三维空间，证明关于四面体的两个共面点定理.

2 性质1的引申及证明

性质1可引申推广为：

定理1过四面体ABCD的棱CD，DA，AB，BC作与已知平面π垂直的平面π1，π2，π3，π4，分别与对棱AB，BC，CD，DA交于点X，Y，Z，W，则X，Y，Z，W四点共面.

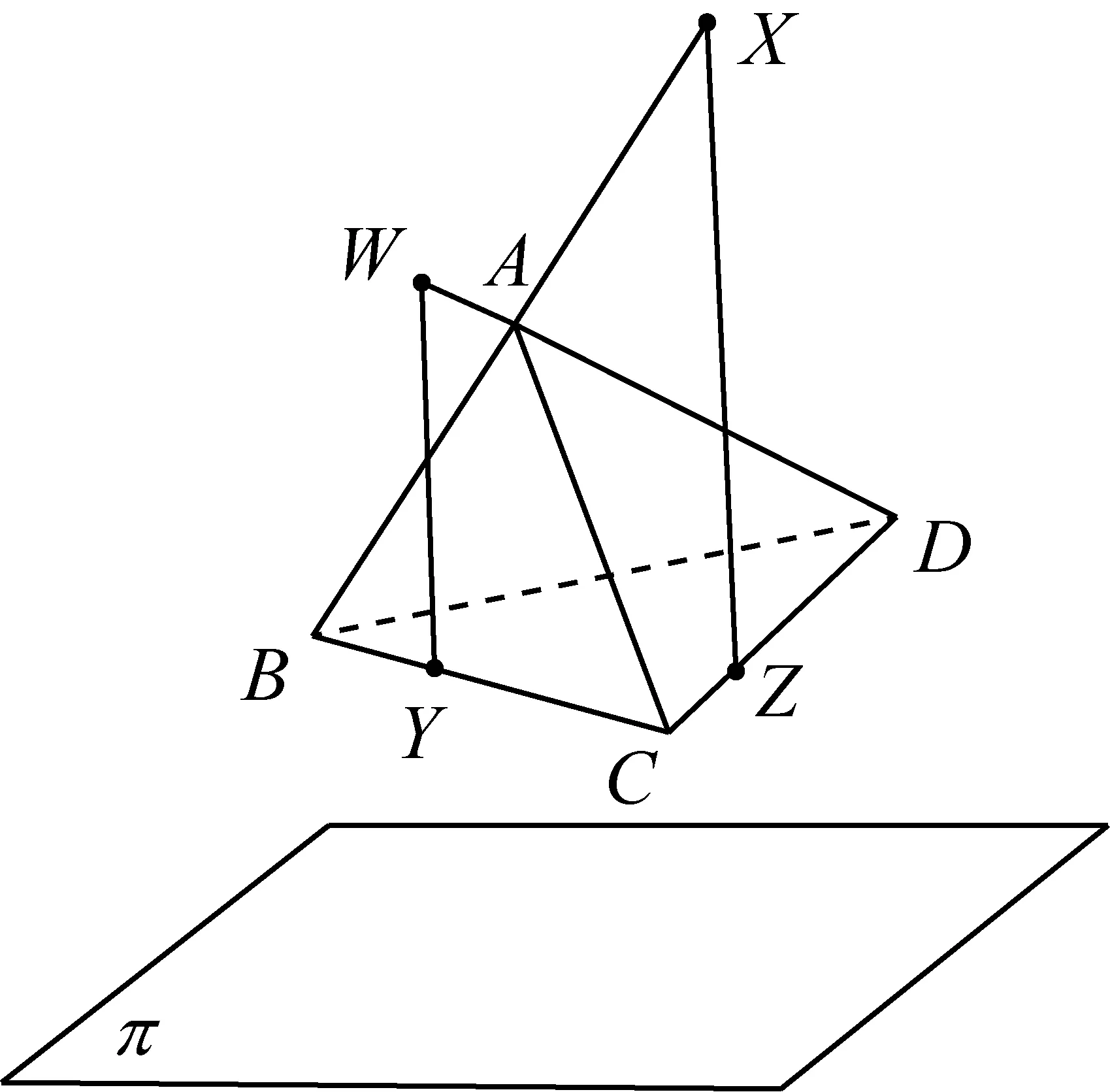
图3

证明如图3，依题设，过CD与平面π垂直的平面π1交AB于X，过AB与平面π垂直的平面π3交CD于Z，则有X∈平面π1，而Z∈CD⊂平面π1，表明直线XZ⊂平面π1；又Z∈平面π3，而X∈AB⊂平面π3，表明直线XZ⊂平面π3，由此可知直线XZ是平面π1与π3的交线，注意到平面π1与π3均与平面π垂直，因此XZ⊥平面π.

同理可证，WY是平面π2与π4的交线，且WY⊥平面π.因此有XZ∥WY，故此X，Y，Z，W四点共面.证毕.

3 性质2的引申及证明

性质2可引申推广为：

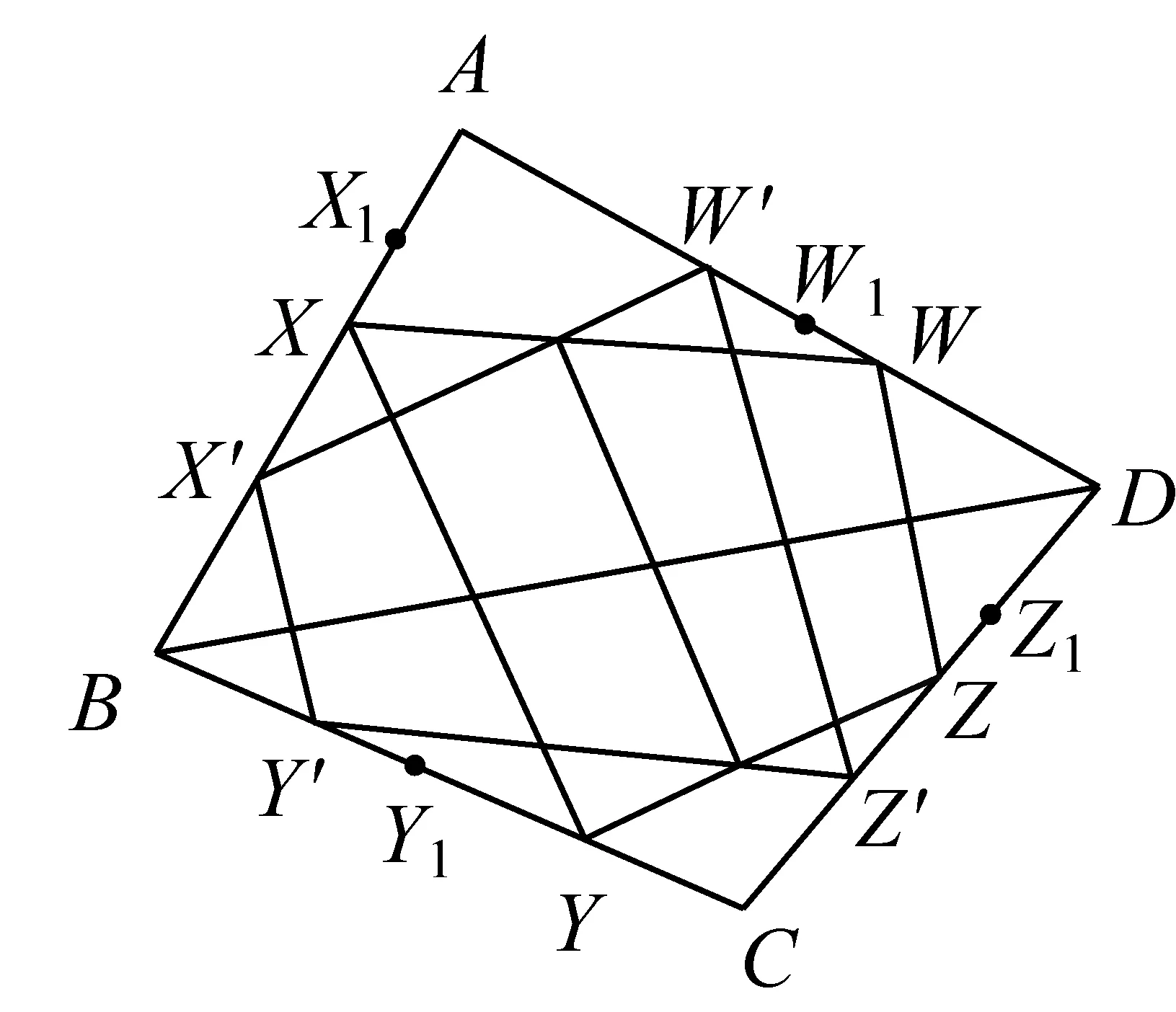
图4

定理2在四面体ABCD中，作两个平面π，π′分别与AB，BC，CD，DA交于点X，Y，Z，W和点X′，Y′，Z′，W′，设平面YZW′交AB于X1，平面ZWX′交BC于Y1，平面WXY′交CD于Z1，平面XYZ′交DA于W1，则X1,Y1,Z1,W1四点共面.

定理2的证明需要下面的引理：

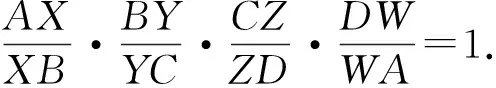
定理2的证明

如图4，由X，Y，Z，W四点共面及引理中的必要性知

①

同理，由X′，Y′，Z′，W′四点共面有

②

由X1，Y，Z，W′四点共面有

③

由X′，Y1，Z，W四点共面有

④

由X，Y′，Z1，W四点共面有

⑤

由X，Y，Z′,W1四点共面有

⑥

将③④⑤⑥四式两边分别相乘，并注意到①、②式就得

根据引理中的充分性知X1，Y1，Z1，W1四点共面.证毕.

4 结语

最后顺便指出，本文中三角形的性质1其实有多种方式引申至三维空间，定理1只是选择了其中一种方式引申所得.有兴趣的读者可以尝试其他方式对它进行引申推广，或许能得到更加优美、有趣的结论.