以“五要”为引领，提升试卷讲评效率

张忠才，梁小梅

（1.甘肃武威市天祝县第二中学，甘肃 武威；2.甘肃武威市天祝县职教中心，甘肃 武威）

一、要即时反馈，突出时效性

每次考试检测结束之后，学生对考试题目及解题思路和方法都有深刻的印象。而且，学生也想知道自己考得怎么样，会主动去查阅试卷。因此，教师应该在很短的时间内完成试卷的批阅，做出试卷分析，及时讲评反馈，这样可达到事半功倍的效果。如果试卷不能及时讲评，当学生把试卷内容忘记了再讲，则不利于学生对错题的纠正和知识的弥补，试卷讲评的效果便会大打折扣。笔者在每次考试结束后，利用多媒体及时公布答案，让学生按照评分标准先自行评分，反思实际分与评估分的差距及其原因。对于那些难度较大，对照答案也很难理解的个别题目，我会把解题思路分析和探究过程以微课的形式提供给学生学习，体现及时性和时效性。

二、要互换角色，突出激励性

不论什么样的课型，教师都应将“激励、呼唤、鼓舞”贯穿于课堂的全过程。在一般情况下，试卷讲评课前，教师自行对试卷答题情况进行分析。而笔者把课前分析试卷、统计错误、查找错因的机会交给学生。通过下面表格收集和整理数据后进行试卷分析。

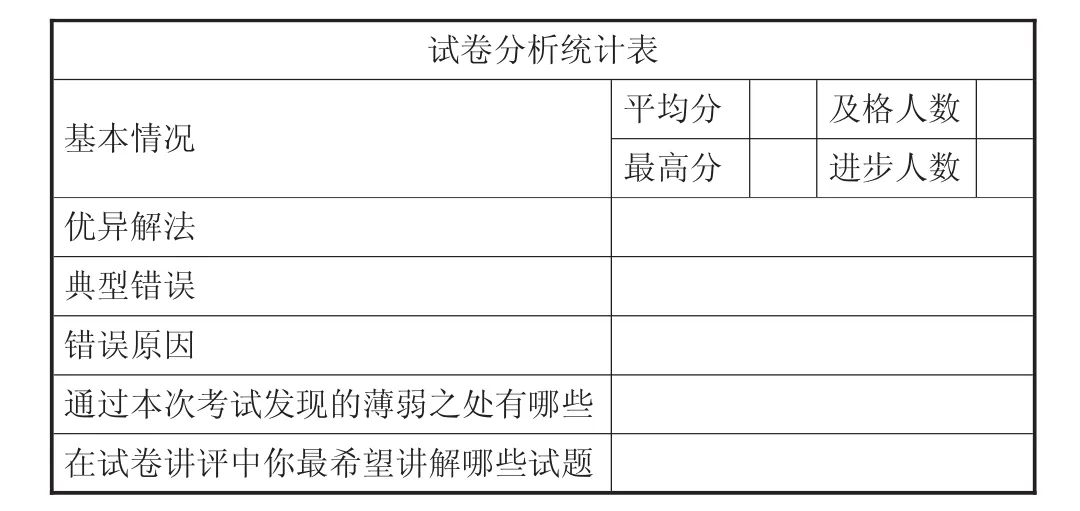
试卷分析统计表基本情况 平均分 及格人数最高分 进步人数优异解法典型错误错误原因通过本次考试发现的薄弱之处有哪些在试卷讲评中你最希望讲解哪些试题

讲评课开始，通过多媒体展示数据分析后的数据信息，让学生上讲台展示自己的思维过程，教师及时评价学生的答卷情况。表扬解题规范、思路清晰、解法独到的学生。对考试成绩不太理想的学生，通过解题思路、运算过程、语言表达方面入手捕捉其闪光点，让其看到自己的点滴进步。这种方式避免了成绩不太理想的学生在心理上产生落差，增强了他们学习数学的信心。

三、要洞察纠错，突出针对性

一份试卷批改下来，通过统计分析，总有一些错误是具有共性的，这类错误题目才是讲评的重点。讲评时不能面面俱到，要选择典型的、学生出错较多的、有代表性的题目来讲解。教师必须在试卷讲评前通过阅读、面批等多种渠道了解真实原因，只有搞清楚学生出错的原因及关节点，讲评才会有针对性，从而提高试卷讲评的效率。

例如：已知a，b，c分别为△ABC的三个内角∠A、∠B、∠C的对边，a=2 且（2+b）（sinA-sinB）=（c-b）sinC，则△ABC 面积的最大值是多少？

像这种题目，学生屡考屡错。经抽查发现，错解原因是学生找不到切入点或者想不到关注点（忽视了基本不等式应用条件）。

【审题过程】切入点：根据题目确定把边角关系转化为边边关系，还是把边角关系转化为角角关系。关注点：利用基本不等式求最值以及利用基本不等式的条件。

四、要借题发挥，突出延展性

对于一道题讲明思路，讲透方法是容易的，但就题讲题是难以提高学生分析问题和解决问题数学能力的。数学讲评时应更加注重的是从一道题中跳出去，拓展些类似的题目，力争讲一题，学生会一串，懂一片，能举一反三，触类旁通。

例如：已知函数f（x）=x3-3x（x∈R），求在点A（2，2）处切线L的方程。

本题利用导数研究“在点”处的切线方程问题，在讲解时可以拓展到利用导数求“过点”切线问题。通过变式讲解，让学生掌握“过点”与“在点”的差异；过点的切线中，点不一定是切点，点也不一定在已知函数图象上，而“在点”处的切线，必以此点为切点。

五、要主次分明，突出典型

试卷讲评绝不能面面俱到，从头讲到尾地讲，而要清楚地了解到学生存在的最突出、最主要的问题是什么，并且对试题逐一分类并恰当分类，根据学情对分析的试题有选择地进行讲解，应选学生在卷面上有独到见解的试题或者出现错误较多的典型例题进行讲评。

六、要回归课本，突出规范性

课本是基础，正所谓“万变不离其宗”，即不论考题如何变化，都要根据课本知识来变。所以，笔者通过试卷讲评来回归课本，掌握每一个定义、定理，以及重要定理的证明过程，不仅仅要知道结论是什么，结论有哪些变化，还要知道结论是怎么来的、怎么用。这样学生在解题过程中才能思路清晰、明确，正确解题。在试卷讲评时，对课本例题和课后练习教师要格外注意，它们是知识的基本应用，也是考题变形的基础，更是解决综合性试题必备的基础训练，更是规范解题的保证。