某型狙击榴弹发射器橡胶缓冲部件对其发射性能影响研究

赵排航， 王瑞林， 李永建， 贾云非， 康小勇

(陆军工程大学石家庄校区 火炮工程系，石家庄 050003)

某型狙击榴弹发射器是一种集面杀伤和破甲效能于一身，遂行狙击和精确打击任务的单兵武器，可有效应对工事或建筑物之后的有生目标及敌轻型装甲车辆等目标。

该武器是一款可抵肩发射的大口径、高精度狙击榴弹发射器，这要归功于其多级多重缓冲机构。其中，机匣尾部与导轨和自动机之间的橡胶缓冲垫对武器系统的性能起了关键作用。但是，橡胶缓冲垫材料的本构关系不仅在静载时体现出一定的非线性，在动载时也具有一定的应变率效应，且不同的橡胶材料，本构模型也有很大差别，这就给模型的理论计算带来了一定难度。

本文以该型狙击榴弹发射器为研究对象，对该发射器的关键部件进行运动分析，建立虚拟样机模型，分别进行静载和动载压缩实验，对橡胶缓冲垫材料的本构关系展开研究，得到该材料在不同平均应变率下的本构关系，根据实际情况在虚拟样机模型中加载合适的本构关系以提高模型的可信性。并对仿真结果进行分析，研究橡胶缓冲垫对系统平稳性和减后坐力的作用，为该发射器进一步的改进研究奠定基础。

1 虚拟样机的建立

该发射器主要由身管与机匣组件、浮动导轨组件、自动机组件、发射机组件、弹鼓、两脚架等组成；由于发射器零部件较多，模型复杂，考虑到Adams软件的建模功能相对较弱，故采用Pro/E软件建立其三维模型，并通过Mechanism/Pro模块导入到Adams软件中以保证模型的精度[1]。

1.1 模型的简化与假设

在研究过程中，主要对武器系统做以下简化与假设：

(1) 忽略对自动机运动影响微小的因素，合并无相对运动的组件，忽略掉小质量非关键零件；

(2) 不考虑所有弹簧的惯性，并根据弹簧的类型，用软件中弹簧阻尼器代替；

(3) 该型发射器为抵肩发射武器，后坐力较小，且仿真计算时考虑射角为零的情况下地面支撑力对射击过程影响较小，故将驻锄与土壤的相互作用问题简化为普通的刚体接触问题。

1.2 约束副的施加

整个发射器系统中共包含10个自由度。构件之间主要的运动包括：发射器与人体的相对运动、身管机匣组件与整体导轨的相对运动、自动机体与机匣的相对运动。身管与机匣连为一体在导轨内部运动，实现身管后坐分担后坐能量，减小后坐力，即身管后坐原理；自动机组件位于机匣内部实现后坐与复进，发射机组件、弹鼓、两脚架等固连于整体导轨。根据系统各机构的运动关系可知，自动机机体的运动x是由导轨在人体抵肩下的运动x1、机匣相对于导轨的运动x2和机体相对于机匣的运动x3叠加的结果，表达式为

x=x1+x2+x3

(1)

武器系统拓扑结构,如图1所示。其主要构件间的运动副,如表1所示。

图1 武器系统拓扑结构

约束副类型构件1构件2平移副身管机匣部件整体导轨平移副自动机机匣接触副击锤机体接触副机体枪尾旋转副机头左(右)闭锁片接触副机头机体接触副抛壳挺抛壳滚轮

1.3 力的施加

在发射器系统中存在的力主要有：弹簧力、接触力、枪膛合力、阻力、支架支撑力和射手抵肩力等。其结构受力简图,如图2所示。

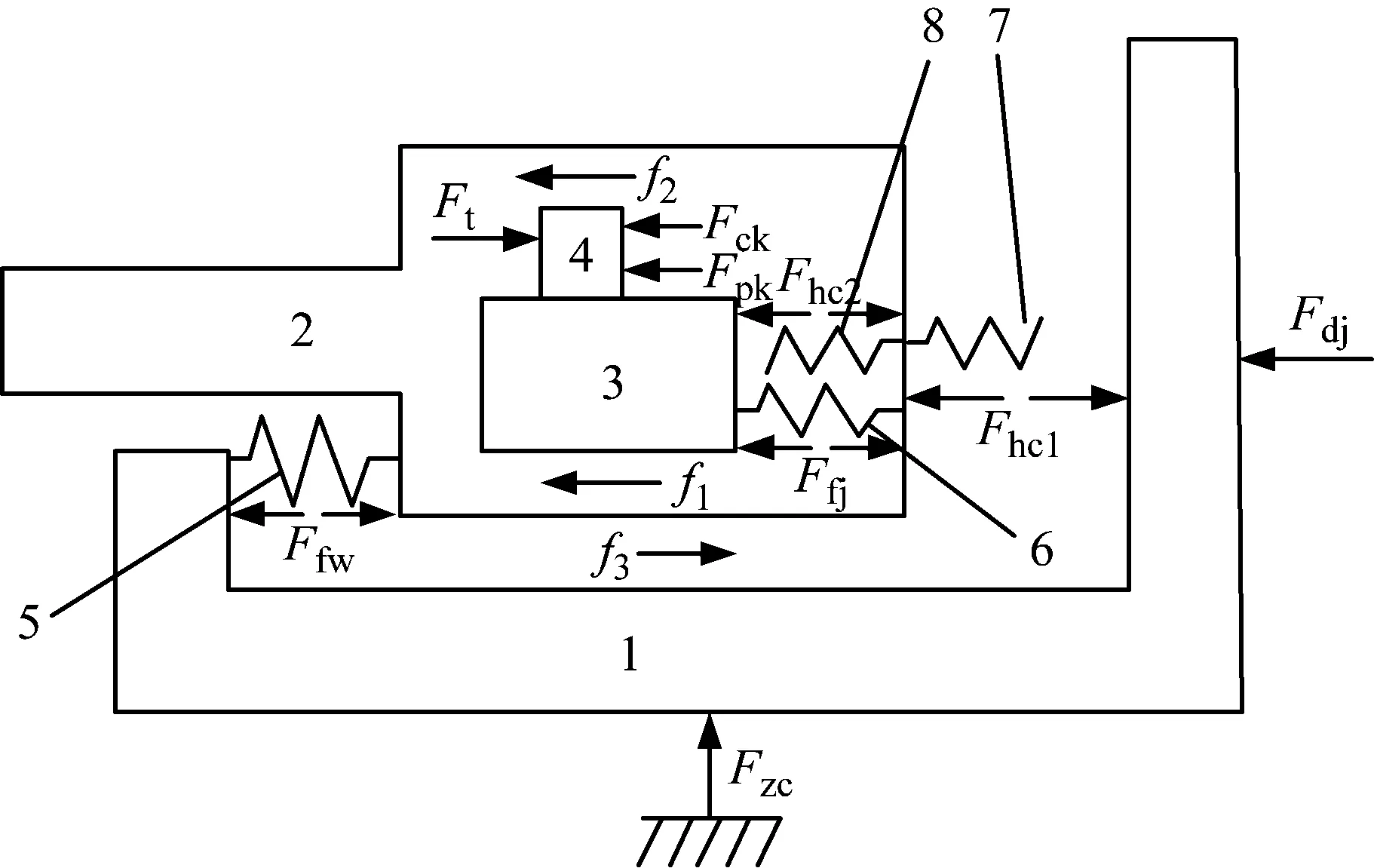
1-整体导轨部件；2-身管机匣部件；3-机体部件；4-机头部件；5-复位簧；6-复进簧；7-缓冲垫1；8-缓冲垫2

图2 发射器系统受力简图

Fig.2 Force diagram of launcher system

图2中，Fdj为抵肩力；Fzc为支架支撑力；Fhc1为机匣尾部与导轨之间缓冲垫的作用力；Fhc2为自动机组件与机匣尾部之间缓冲垫的作用力；Ffj为复进簧力；Ffw为复位簧力；Ft为内膛合力；Fck为抽壳阻力；Fpk为抛壳阻力；f1为机体与机匣间的摩擦力；f2为机头与机匣间的摩擦力；f3为机匣与导轨间的摩擦力。

1.4 枪膛合力计算

根据该武器所用弹药的相关参数，运用内弹道理论，计算得到内弹道时期平均膛压，膛底压强与平均膛压关系式为[2]

(2)

式中：ω为装药量；φ1为阻力系数；q为弹丸质量；p为平均膛压；pt膛底压强。

后效期的计算公式为[3]

p=pke-At

(3)

式中：p为后效期膛内的平均压强；pk为后效期开始时膛内的平均压强；e为自然对数的底；t为从后效期开始算起的时间；A为常系数。

枪膛合力的计算公式为

Ft=pt·S

(4)

式中：S为身管横截面积。

由此得到的枪膛合力曲线,如图3所示。

1.5 边界条件的确定

人体阻尼和弹性都具有明显的非线性，它取决于施加在人体上外力的幅度。研究表明[4]小幅度冲击时人体的响应可视为线性问题，狙击榴弹发射器作为抵肩发射武器，主要依靠各缓冲机构吸收后坐能量，对射手的冲击较小，因此，采用以集总参数表示的线弹性时不变系统模拟人体抵肩作用。抵肩参数模型,如图4所示。

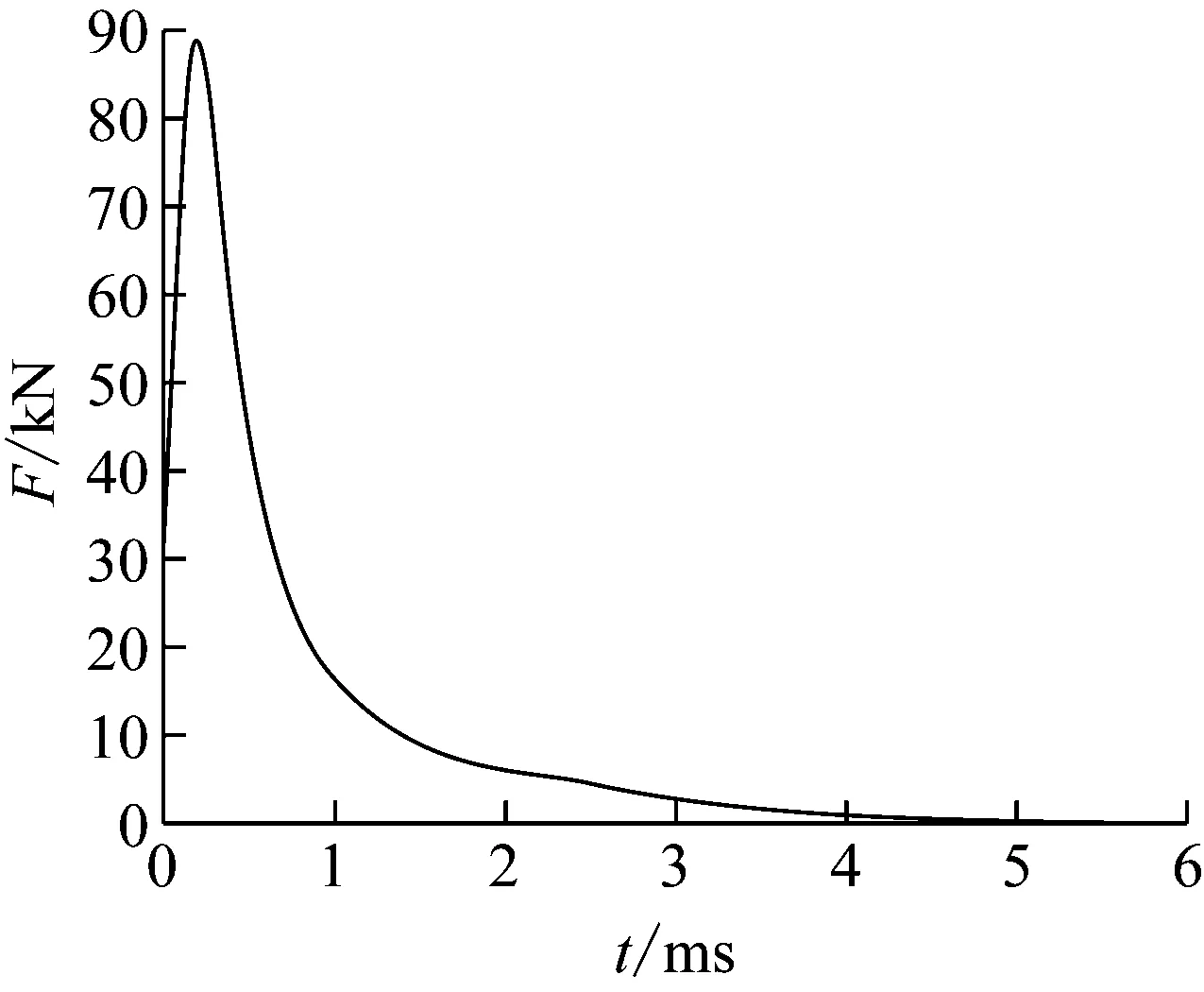
图3 枪膛合力

图4 抵肩参数模型

通过系统识别的方法，求出了该系统最小方差意义下的参数

(5)

2 橡胶缓冲垫作用力

该榴弹发射器作为一款抵肩发射武器，其多级多重缓冲机构大幅度减小了武器的后坐力。在该武器的自动机与枪尾和枪尾与导轨之间均安装有橡胶缓冲垫，分别对两处的撞击起缓冲作用。如何加载这两级缓冲作用中的橡胶材料作用力称为建立虚拟样机的关键。

橡胶材料是由长链、大分子和网状交连结构所构成的超弹性材料[5]，也是一种不可压缩材料，在压缩过程中体积和密度保持不变，且其应力应变关系较金属材料具有更强的非线性。橡胶部件在一个加载循环中一部分能量会通过热能形式被耗散掉，故其加载和卸载曲线是不同的，这种现象称为迟滞现象[6]。

由于Adams软件中零部件均作为刚体来处理，无法模拟其变形与作用力的关系，橡胶缓冲垫的变形与作用力又对武器系统射击过程起着关键作用。为了找到橡胶缓冲垫在虚拟样机中合适的加载方式，保证武器系统动力学仿真的准确性，对该材料的本构模型进行实验研究。

在动力学仿真模型中，橡胶缓冲垫的缓冲作用直接体现就是对其所连接的部件间相互作用力，其作用过程为动态加载的压缩和回弹过程。为了研究不同加载速率对其本构关系的影响，分别采用力学万能试验机和霍普金森杆对橡胶缓冲垫做静载和动载实验。

2.1 静载实验

在静载实验中，试件的作用面积和原始厚度均为已知，只需采集加载力与压缩位移的关系即可得到应力应变的关系，计算公式如下

(6)

式中：σ为应力；F为作用力；S为试件的原始横截面积；ε为应变；Δl为压缩位移；L为试件的原始厚度。

实验采用电子万能试验机，采用2 mm/min的加载速度近似静态加载，加载位移8 mm，采用加载再卸载的方式，采集压缩和回弹位移及载荷数据，经过数据处理得到缓冲垫静态加卸载应力应变曲线,如图5所示。

图5 静态加卸载应力应变曲线

2.2 动载实验

在武器射击过程中，榴弹击发后自动机在闭锁状态下带动身管机匣部件后坐，后坐到位后枪尾通过缓冲垫与导轨接触并相互作用，接触时后坐速度大约为10 m/s，考虑到橡胶材料的力学特性对应变率比较敏感，故采用霍普金森杆实验设备来研究该橡胶材料在不同应变率下的力学特性。霍普金森杆通过入射杆和透射杆的应变测量电路采集动载过程中入射波、反射波和透射波信号，根据一维应力波理论，可以推导出试件中应变率、应变和应力分别为[7-15]

(7)

式中：C为弹性波在杆中的波速；εI(t)、εR(t)、εT(t)分别为试件入射波、反射波、透射波的应变值；E为杆的弹性模量；A为杆的截面积。

通过调整发射杆的速度加载不同的载荷，分别记录入射波、反射波和透射波曲线，经过数据处理可得到应力应变曲线和应变率曲线，为了定量分析不同应变率对材料特性的影响，取应变率曲线峰值平台的平均值为平均应变率，得到橡胶缓冲垫在不同平均应变率下的加卸载应力应变关系曲线，如图6所示。不同平均应变率下的加载应力应变关系曲线对比，如图7所示。

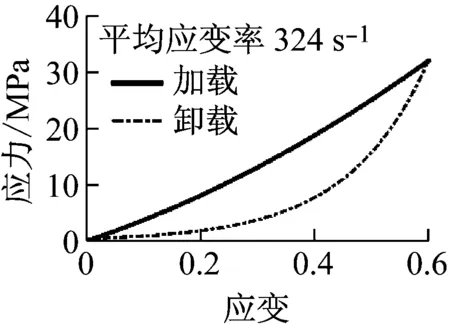
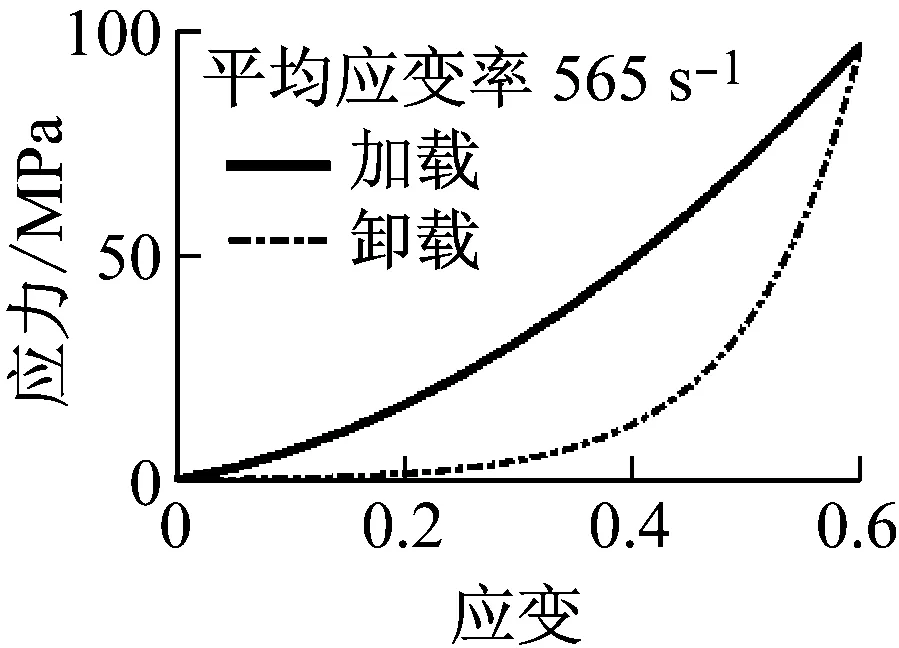
图6 不同平均应变率下的加卸载应力应变曲线

Fig.6 Loading and unloading stress-strain curve with different average strain rates

图7 不同平均应变率下的加载应力应变曲线

由图5和图6可知，无论是静载还是动载下，该橡胶缓冲垫材料均出现迟滞现象，表明材料具有迟滞特性。由图7可知，该橡胶材料的本构关系受平均应变率影响较大，且平均应变率越大发生相同应变时应力就越大，宏观上表现为材料越来越硬，强度越来越大。

根据该发射器的靶场实验数据计算两个橡胶缓冲垫的射击过程平均应变率，得到机匣尾部与导轨之间缓冲垫平均应变率约为580 s-1，自动机与机匣尾部之间缓冲垫应变率约为310 s-1，故采用四组动载实验中应变率为565 s-1和324 s-1的本构关系分别添加到机匣与导轨之间缓冲垫和自动机与机匣之间缓冲垫；根据缓冲垫的实际尺寸，计算出轴向压缩位移与作用力的关系，在虚拟样机模型中添加两个marker点，将缓冲垫变形作用面轴向位移与作用力关系导入到Adams软件成为软件可以调用的spline函数，以两点间x轴距离为变量调用spline函数值；由于该橡胶材料压缩和回弹过程本构关系不一致，故在动力学仿真软件中采用IF函数判断两作用部件的相对速度将缓冲垫压缩或回弹的作用力加载到其作用部件上。作用力函数表达式如下：

IF(VX(MARKER_840)-VX(MARKER_802): AKISPL(DIM(DX(MARKER_770,MARKER_777), 0),0,SPLINE_13,0),74675,AKISPL(DIM(DX(MARKER_770, MARKER_777), 0),0,SPLINE_11, 0))

由此，建立了发射器系统的虚拟样机模型。

3 自动机运动分析与校核

该型狙击榴弹发射器之所以能够抵肩发射，主要在于其自动机组件与机匣、导轨在多级缓冲作用下的运动耦合对减小武器后坐力、提高平稳性起了关键作用。

3.1 自动机运动分析

根据虚拟样机仿真结果，该发射器射击循环的机匣、导轨和机体的速度曲线,如图8所示。将发射器膛口方向定为运动的负方向，武器击发后，自动机在闭锁状态下带动机匣共同后坐，在标识1处机匣后坐到位，尾部缓冲垫撞击导轨，自动机机体在惯性作用下继续后坐，此时闭锁片开锁，机体将带动机头继续后坐；标识2处表示机匣与导轨接触后导轨在缓冲垫作用力下开始加速后坐，在抵肩力的作用下，其速度在短暂上升后迅速下降并向前运动；机匣在第一次与导轨接触并相互作用后仍然以缓慢的速度继续后坐，在复位簧的作用下后坐速度逐渐减小直至向前复位，在标识3处复位到位，之后与导轨共同运动；自动机不断后坐，在标识4处后坐到位与机匣尾部接触并相互作用，致使机匣再次相对于导轨后坐进而压缩复位簧，导轨则在复位簧力的作用下逐渐加速向前运动；自动机在复进簧力的作用下不断加速复进，机匣和导轨在复进簧力、复位簧力和抵肩力的共同作用下在标识5处复位到位，之后共同发生微小运动；标识6处为自动机复进到位，机头撞击身管尾端，机体继续复进关闭闭锁片，图8中速度波动即为闭锁过程，之后速度降为零，整个射击过程完成。射击循环中机匣、导轨和机体的位移曲线,如图9所示。

图8 机匣、导轨和机体速度曲线

图9 机匣、导轨和机体位移曲线

3.2 自动机运动速度校核

为了进一步说明仿真结果的可信性，将自动机机体的几个具有代表性的运动瞬时速度仿真结果与实验数据做了对比，如表2所示。

表2机体运动速度仿真值与实验值对比

Tab.2ComparisonofsimulationvaluesofAutomaticbodywithexperimentalresults

机体速度仿真计算值/(m·s-1)实验数据/(m·s-1)误差/%后坐最大10.3510.733.7后坐到位5.485.928.0复进开始0.340.333.0复进到位4.474.766.5

从表2可知，自动机机体的运动速度仿真结果与实验数据的误差均小于10%，符合虚拟样机建立要求，仿真结果具有可信性。

4 仿真结果分析

4.1 缓冲垫对系统平稳性的影响

为了验证橡胶缓冲垫对武器系统平稳性的影响，对有无橡胶缓冲垫的两种情况下机体、机匣与导轨的运动速度曲线进行对比，分别如图10～图12所示。

图10 机体速度对比曲线

Fig.10 Speed contrast curve of automatic body

图11 机匣速度对比曲线

Fig.11 Speed contrast curve of automatic casing

图12 导轨速度对比曲线

由图10可知，有无橡胶缓冲作用对机体的速度影响并不大，标识1处是在自动机后坐到位与机匣尾部接触后速度迅速减小，有缓冲比无缓冲时速度减幅度略大是由于在缓冲垫作用下，自动机与机匣之间的缓冲力作用时间更长，自动机所获得复进冲量也较大。

由图11可知，标识1处为机匣后坐到位自动机开锁过程，开锁后出现速度短暂增大是由于开锁时机体由于惯性后坐带动机头挤压闭锁片，闭锁片靠与机匣的作用力在开锁方向上的分力实现开锁，而在与之垂直方向上的分力则带动机匣短暂加速，开锁完成后作用力消失；由于缓冲垫作用力要小于无缓冲时刚体接触的作用力，故有缓冲比无缓冲时机匣与导轨接触后减速较慢；但由于有缓冲时缓冲作用时间较长，机匣所受缓冲作用力的冲量较大，故自动机开锁完成后有缓冲时机匣速度比无缓冲时小；机匣从自动机开锁完成到机匣向前复位完成是在复位簧的作用下进行的，这段时间内机匣所受外力的冲量是一定的，与有无缓冲无关，根据动量定理，标识2处有缓冲时机匣速度比无缓冲时大是合理的。

由图12可知，有无缓冲作用对导轨的运动影响较大，在标识1处，由于无缓冲时刚体之间的作用力要比缓冲垫作用力较大，故无缓冲时在机匣后坐到位与导轨接触后导轨的速度上升较快且最大速度较大，无缓冲最大速度是有缓冲的1.13倍；在标识2处，无缓冲时导轨速度出现波动而有缓冲时未出现；发射器的两脚架、弹鼓、发射机、瞄准镜等部件均固定于导轨，无缓冲作用时发射器整体后坐最大速度及振动较大。这表明，橡胶缓冲垫有效减小刚性接触对武器系统的影响，减少构件振动，提高系统的平稳性。

4.2 缓冲垫对后坐力的影响

为了更加直观的说明橡胶缓冲垫的作用，将虚拟样机中模拟抵肩力的刚度阻尼器的作用力当做后坐力，对有无橡胶缓冲垫的两种情况下的后坐力曲线进行对比。由图13可知，有缓冲作用时后坐力峰值约为6.1 kN，而无缓冲时后坐力峰值约为9.4 kN，是无缓冲的1.54倍；无缓冲时后坐力曲线的波动也明显较大。这表明缓冲垫可有效降低武器后坐力，提高人机工效。

图13 后坐力对比曲线

5 结 论

本文运用静载和动载实验对橡胶缓冲部件的本构关系进行了研究，结果表明：该材料的本构关系具有明显的非线性、迟滞特性及应变率效应，且应变率越大发生相同应变时应力就越大，表现为材料的强度越大；根据实际工况中应变率，在虚拟样机中采用以距离为变量的方式加载合适的作用力。

采用动力学仿真的方法，对比分析了有无橡胶缓冲垫作用下机体、机匣和导轨的速度曲线和后坐力曲线，分析结果表明：橡胶缓冲垫的缓冲作用可有效减小刚性接触对系统的影响，提高平稳性；有效减小后坐力，提高人机工效。