循环爆破荷载作用下小净距隧道中夹岩的累积损伤特征分析

曹 峰， 凌同华， 李 洁， 黄 阜

(1. 长沙理工大学 土木工程学院， 长沙 410114； 2. 长沙理工大学 桥梁工程高校重点实验室， 长沙 410114;3. 湖南省交通规划勘察设计院有限公司， 长沙 410008； 4. 新余学院建筑工程学院， 江西 新余 338004)

近年来，分岔隧道作为一种新型的隧道结构形式逐渐引起了人们的关注[1]，它包含连拱段、小净距段和分离段三种隧道结构形式，其特点是能够适应多变的地质地形条件，在展线困难和桥隧过渡工程中具有较好的应用前景。其中，小净距段是连接连拱段与分离段的关键工程。爆破开挖时，爆炸产生的能量一部分用来破坏介质，形成隧道，而其它大部分能量传递给围岩，造成保留岩体的损伤和破坏。国内外学者对岩体的爆破损伤进行了卓有成效的研究，凌同华等[2]提出基于多元判别分析理论的岩体爆破震动损伤安全判据方法；刘永胜等[3]分析了隧道松动圈的形成过程；左双英等[4]采用数值模拟方法探讨了圆形隧道的围岩损伤分布规律；陈俊桦等[5]采用数值模拟和现场试验手段研究了大型地下厂房的爆破损伤影响范围；Malmgren等[6-7]研究了矿山开采区的损伤分布范围以及岩体的损伤演化特征。但其结论主要是在单孔装药、单次爆破的条件下实现的。事实上，隧道的爆破作业往往是循环推进式重复爆破，对保留岩体同一部位的多次扰动极易导致微裂纹的扩展，使力学性能不断劣化，形成累积损伤。相关学者也对爆破荷载作用下岩体的累积损伤进行了探索[8-11]，但针对循环爆破荷载作用下小净距隧道中夹岩的累积损伤特征研究还较少，尚缺乏围岩的累积损伤安全判据。因此，研究循环爆破荷载作用下围岩的累积损伤特征具有重要意义。

本文结合湘西六月田分岔隧道小净距段的工程特点，采用数值模拟和现场测试相结合的方法，研究多循环推进式爆破开挖诱发的保留岩体累积损伤演化规律，探讨单次爆破和多次爆破荷载对中夹岩的累积损伤效应，分析装药量、损伤范围与振动速度三者的相互关系。

1 工程概况

六月田隧道位于湘西自治州永顺县，隧道左线长1 010 m(K10+445～K11+455)，右线长1 015 m(YK10+440～YK11+455)，属长隧道。隧道出口为分岔式隧道，出口前方与猛洞河大桥相连。工程所处路段属剥蚀溶蚀低山地貌，出口段山体自然坡度为30°～35°，地形起伏大。隧道范围内岩石主要为微风化灰岩[12]。其中，小净距段隧道全长77 m，埋深25～46 m，中夹岩净距3～6 m。隧道围岩以Ⅳ级为主。小净距段隧道设计断面，如图1所示。

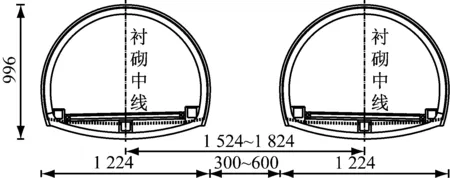
图1 六月田隧道小净距段设计断面图(cm)

六月田隧道采用新奥法设计和施工，小净距段隧道分上下台阶开挖，以减少爆破振动对保留岩体的影响，开挖完成后及时进行初期支护。上台阶开挖采用楔形掏槽的爆破方法，炮孔直径42 mm。周边眼采用光面爆破，间距50 cm。炸药选用2#岩石乳化炸药。

2 爆破损伤的数值模拟

2.1 计算模型及参数

根据六月田分岔隧道小净距段的实际工程尺寸，采用LS-DYNA有限元程序建立三维模型。根据圣维南原理，模型边界范围一般取3倍～5倍洞径[13]。因此，三维计算模型的边界范围取：左右宽度X方向为-55 m，55 m；Y方向上边界至地面，下边界为30 m；隧道纵向Z方向为100 m。模型的上边界设置为自由边界，左、右边界及下边界设置为无反射边界。岩体、炸药和空气的单元类型均为SOLID164，整个模型共划分180 622个单元，173 827个节点。计算模型及网格划分如图2所示。

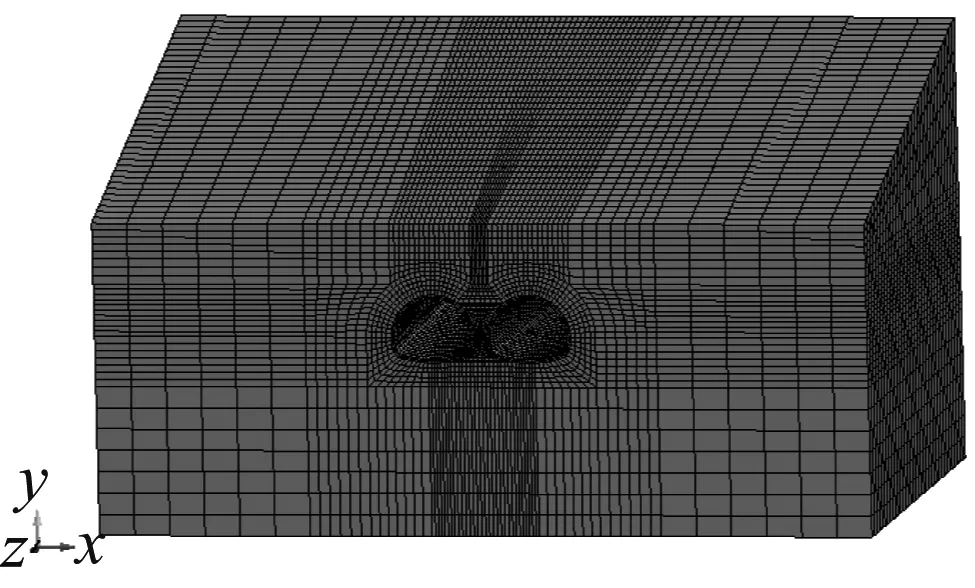
2.2 岩石的本构模型

岩石采用HJC(Holmquist-Johnson-Cook)本构模型，该模型综合考虑了高应变率、高压效应和大应变，主要用于岩石和混凝土的损伤模拟。其等效屈服强度是压力、应变率和损伤的函数，而压力是体积应变的函数。HJC模型的强度可以采用规范化的等效应力描述为[14-17]

(1)

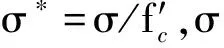
(2)

式中：ΔεP和ΔμP分别为等效应变塑性增量和等效体积应变增量；f(P)=ΔεP+ΔμP为常压P下材料断裂时的塑性应变；T*为材料所能承受的规范化最大拉伸应力；D1和D2为损伤常数。

HJC本构模型参数包括极限面参数、损伤参数和压力参数等。根据相关文献对石灰岩的实验数据和现场的工程地质勘查资料，石灰岩的 HJC本构模型参数见表1。其中ρ0为岩石密度 (kg/m3)，T为最大静水压力(GPa)；SFmax为岩石所能达到的最大断裂强度；G为剪切模量(GPa)；EFmin为岩石破碎的最小塑性应变；D1和D2为岩石的损伤常数；K1，K2，K3为实验确定的相关材料参数；Pcrush和Plock分别为失效压力和极限体积应力(GPa)；μcrush和μlock分别为失效体应变和极限体积应变。

表1 HJC本构模型参数

2.3 炸药的控制方程及材料参数

炸药的爆炸过程采用JWL状态方程进行模拟。其表现形式为

(3)

式中：A，B为材料常数(GPa)；R1，R2，ω为状态方程的常数；V为相对体积；E0为初始内能密度(GPa)。

根据林从谋等的研究，在数值模拟中将炸药按集中装药方式进行分析，验算结果是安全的，并偏于保守。结合小净距隧道现场的开挖爆破方案，小净距段上台阶装药量取43.5 kg。数值模拟中采用集中耦合装药方式，利用网格划分方法将相同重量的炸药单元模型布置在后行隧道上台阶中部偏下，即掏槽眼处。炸药模型距离上台阶底板1～1.5 m。炸药采用MAT_HIGH_EXPLOSIVE_BURN模型模拟，定义*EOS_JWL关键字为炸药的状态方程。表2为炸药材料及状态方程参数。

表2 炸药材料及状态方程参数

2.4 计算结果与分析

考虑到施加单次爆破荷载难以准确的计算围岩的累积损伤范围，本次模拟采用重启动技术，将前一次的爆破损伤结果作为下一次爆破的初始条件，利用*stress_intialization和*delete_part 等关键字实现多次爆破荷载对岩体的累积损伤[18]。结合小净距隧道的实际情况，选取K11+390作为监测断面，模拟开挖面K11+402，K11+398，K11+394，K11+390，K11+386，K11+382连续爆破时，监测断面保留岩体的累积损伤范围及程度。数值模拟计算的累积损伤范围并不包括隧道开挖卸载造成的损伤。为便于分析，将上述开挖面分别定义为第1次～第5次爆破。监测断面布置示意图和累积损伤演化过程，如图3、图4所示。

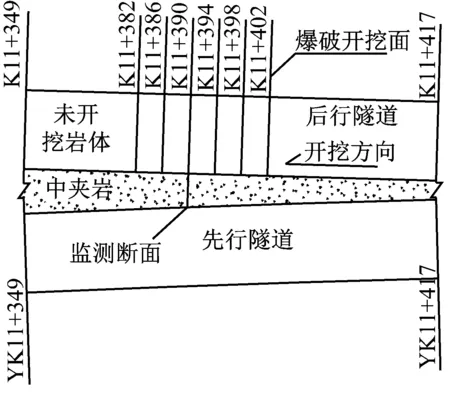
图3 监测断面布置示意图

由图4可知，第1次爆破后，监测断面处保留岩体的损伤范围均<0.3 m。第2次爆破后，监测断面处保留岩体的损伤范围仅小幅增长，最大值为0.6 m。第3次爆破后，中夹岩侧拱肩和拱腰处保留岩体的损伤范围分别为0.9 m和0.7 m。第4次爆破后，保留岩体的损伤范围显著增加，中夹岩侧拱肩、拱腰和拱脚的最大值分别为3.2 m、2.2 m和2.9 m。随着爆破开挖面的持续推进，保留岩体的损伤范围增长幅度较小，至第6次爆破后，最大损伤范围出现在中夹岩侧拱肩与拱腰结合处，为3.6 m。中夹岩侧拱腰的损伤范围为2.4 m。表3为单次爆破与多循环推进式爆破荷载作用下围岩的损伤范围。单次爆破为距离监测断面最近的爆破开挖面单次进行的爆破。

表3 单次爆破和多次爆破条件下围岩的损伤范围

由表3可知，多次爆破后，保留岩体的平均损伤范围增加了39.1%。可以看出，多循环推进式爆破荷载作用下，中夹岩的累积损伤效应最为明显。图5为K11+402～K11+382段围岩的三维累积损伤云图。

(a) 第1次爆破后

(b) 第2次爆破后

(c) 第3次爆破后

(d) 第4次爆破后

(e) 第5次爆破后

(f) 第6次爆破后

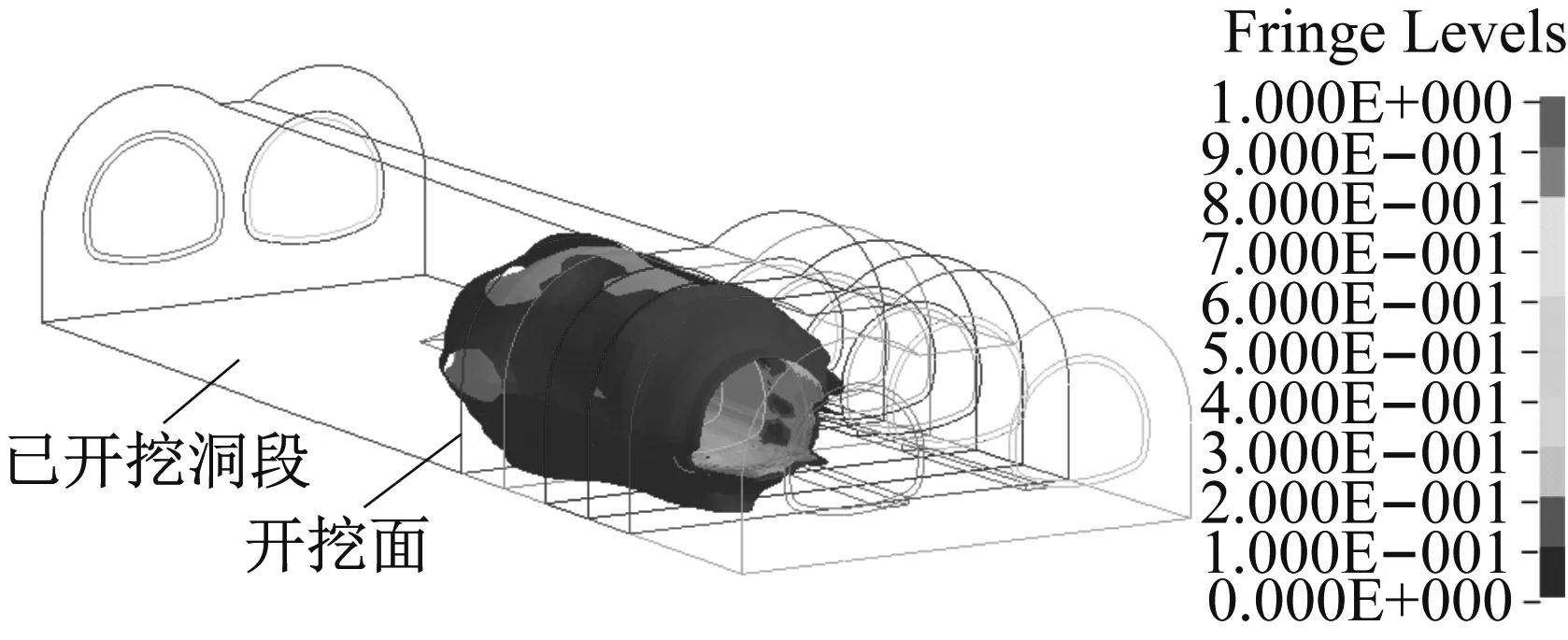
图5 三维累积损伤云图

可以看出，循环爆破开挖对纵轴线上已开挖洞段的保留岩体也造成了累积损伤。经计算，隧道开挖面后方纵轴线上的损伤长度为2.1 m，较单次爆破时的1.6 m延伸了0.5 m。相比单次爆破，循环爆破荷载对开挖面后方纵轴线上造成的损伤长度增加了31.3%。

后行隧道中夹岩侧拱肩、拱腰和拱脚的损伤范围、损伤变量与爆破次数的关系，如图6、图7所示。

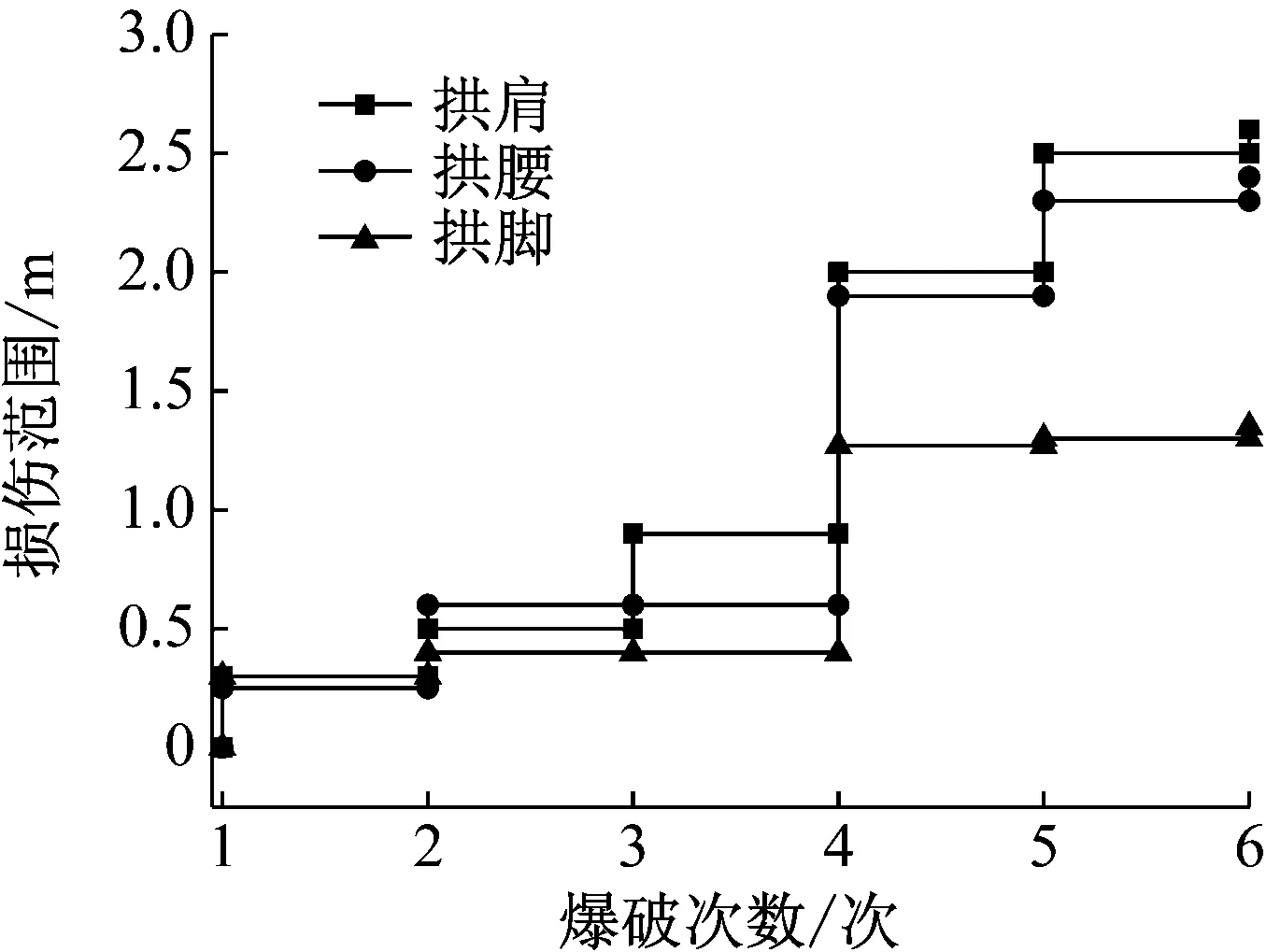
图6 损伤范围与爆破次数的关系

图7 累积损伤变量与爆破次数的关系

从图6和图7可知，拱肩的损伤范围和损伤变量最大。同时，第3次和第4次爆破对围岩造成的损伤范围增量和损伤变量增量较大，损伤效应较明显。

通过改变计算模型装药量，在单次爆破和循环多次爆破荷载作用下中夹岩的最大损伤范围，如表4所示。

分析可知，在装药量相同的情况下，循环多次爆破对中夹岩造成的累积损伤范围明显大于单次爆破时的损伤范围。考虑到装药量9.3 kg时的变化率具有特殊性，选取其它装药量条件下的数据统计可知，多次爆破引起的平均累积损伤范围比单次爆破时增加了47.1%。

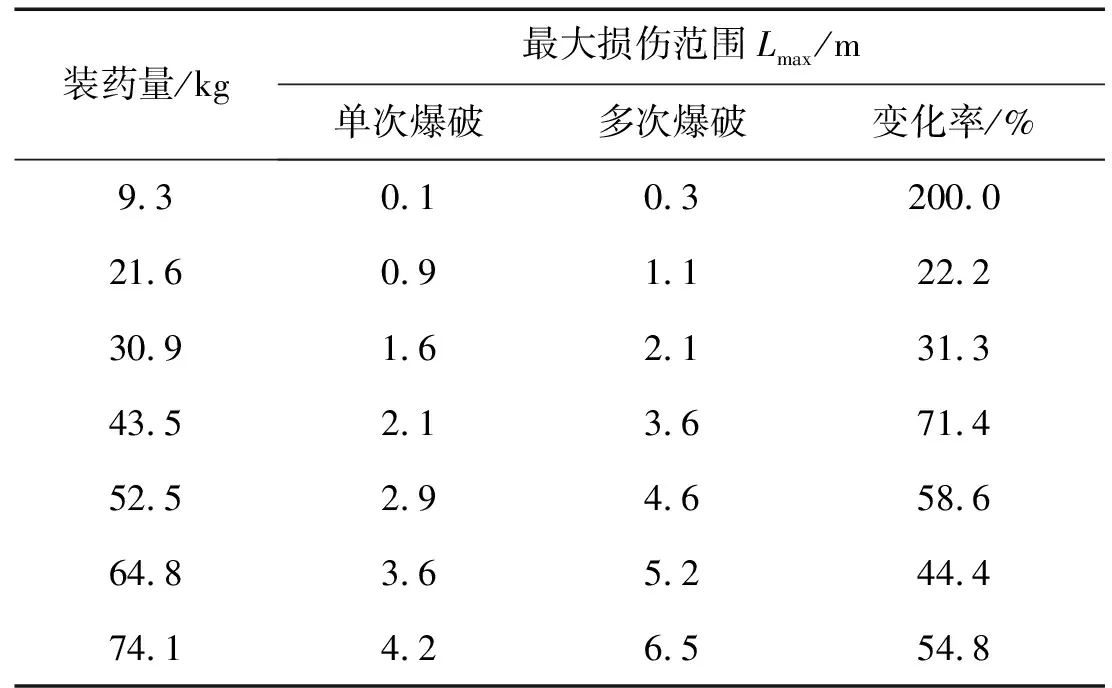
表4 不同装药量条件下中夹岩的最大损伤范围

由爆破近区衰减规律可知[19-20]，损伤范围为装药量的幂函数。根据两者的关系，对表4的数据进行拟合，得到不同装药量与多次爆破最大损伤范围的关系曲线，如图8所示。

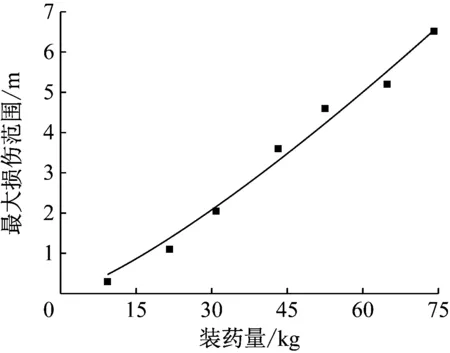
图8 装药量和最大损伤范围的关系

将图8的数据进行拟合，可得

Lmax=0.028Q1.265

(4)

式中：Q为装药量(kg)；Lmax为最大损伤范围(m)。

结合表4，采用数值计算模型，通过施加单次爆破荷载和循环多次爆破荷载，提取中夹岩最大损伤范围处临界损伤部位节点的振速，即中夹岩的临界损伤峰值质点振速，如表5所示。表中临界损伤峰值质点振速Vcr为最大损伤范围Lmax所对应的质点振速。

从表5可知，循环多次爆破作用下中夹岩的平均临界损伤峰值质点振速比单次爆破条件下中夹岩的平均临界损伤峰值质点振速降低了34.5%。

根据柱面波理论及长柱状装药的子波理论，损伤区质点振速衰减规律可表示为[21]

(5)

式中：V为损伤区质点振速(cm/s)；k′为与岩石介质、装药方式相关的系数；L为损伤区某点至装药几何中心的水平距离(m)；m为衰减系数。

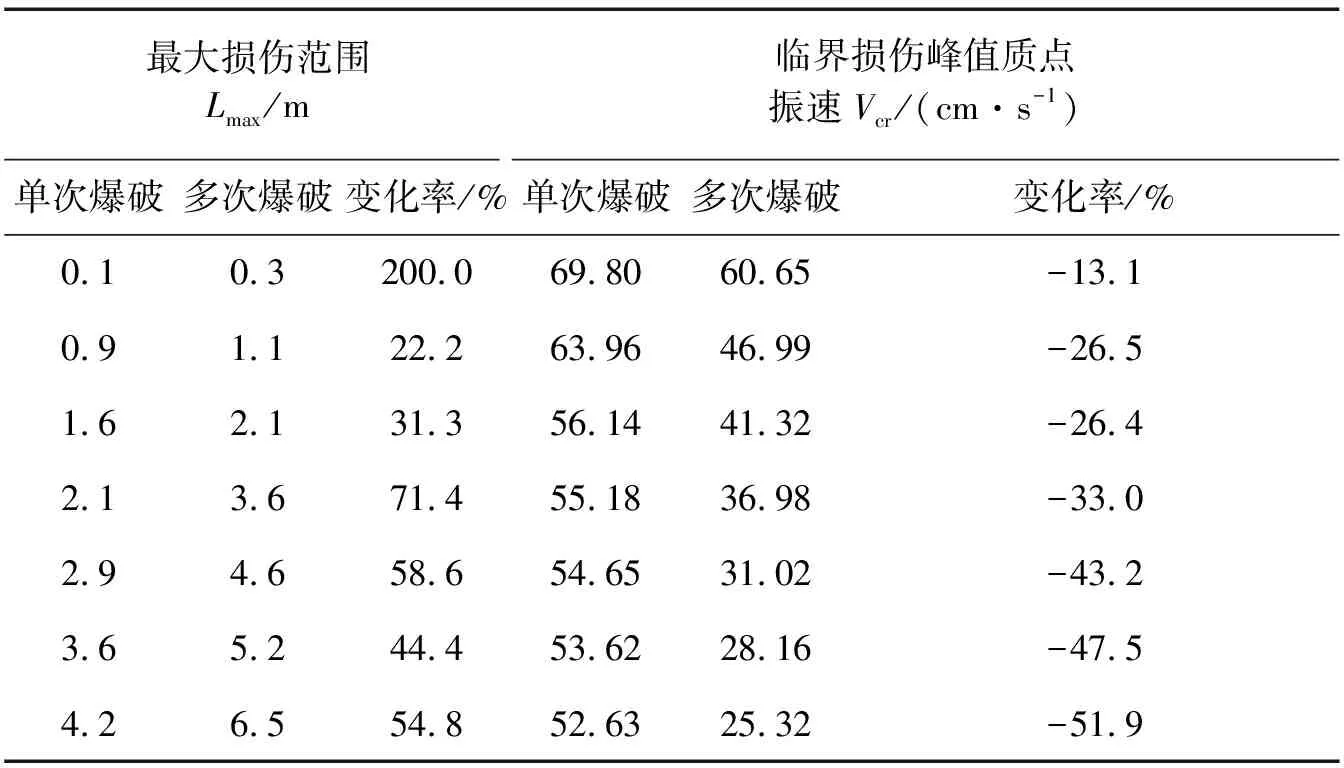
表5 最大损伤范围及对应的临界损伤峰值质点振速

从式(5)可知，损伤区质点振速与损伤范围具有相关性。结合式(5)，对表5中多次爆破荷载作用下的临界损伤峰值质点振速Vcr和最大损伤范围Lmax进行回归拟合，得到两者的关系，如图9所示。

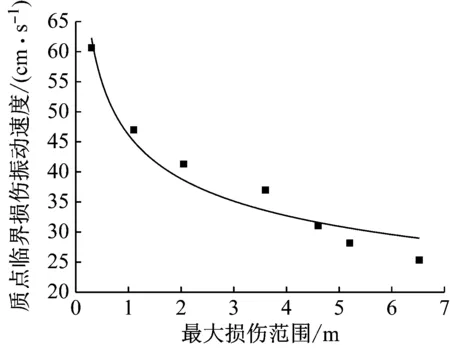
图9 最大损伤范围与质点临界损伤振速的关系

将图9的数据进行拟合，得到最大损伤范围Lmax与临界损伤峰值质点振速Vcr之间的关系为

(6)

联立式(4)和式(6)，可得，

(7)

由式(4)～式(7)可知，已知单循环装药量可以求出多次爆破作用下中夹岩的最大损伤范围和临界损伤峰值质点振速。

综上所述，相比单次爆破荷载作用下围岩的质点临界损伤振速，采用该方法得到的多循环推进式爆破荷载作用下的临界损伤峰值质点振速，能更准确的反映围岩真实损伤状况。

3 现场测试及验证

3.1 监测方案

根据小净距隧道的空间布局和岩体的力学性质，选取Ⅳ级围岩先行隧道侧中夹岩作为监测部位，监测断面桩号为K11+390，声波测试孔的布置，如图10所示。

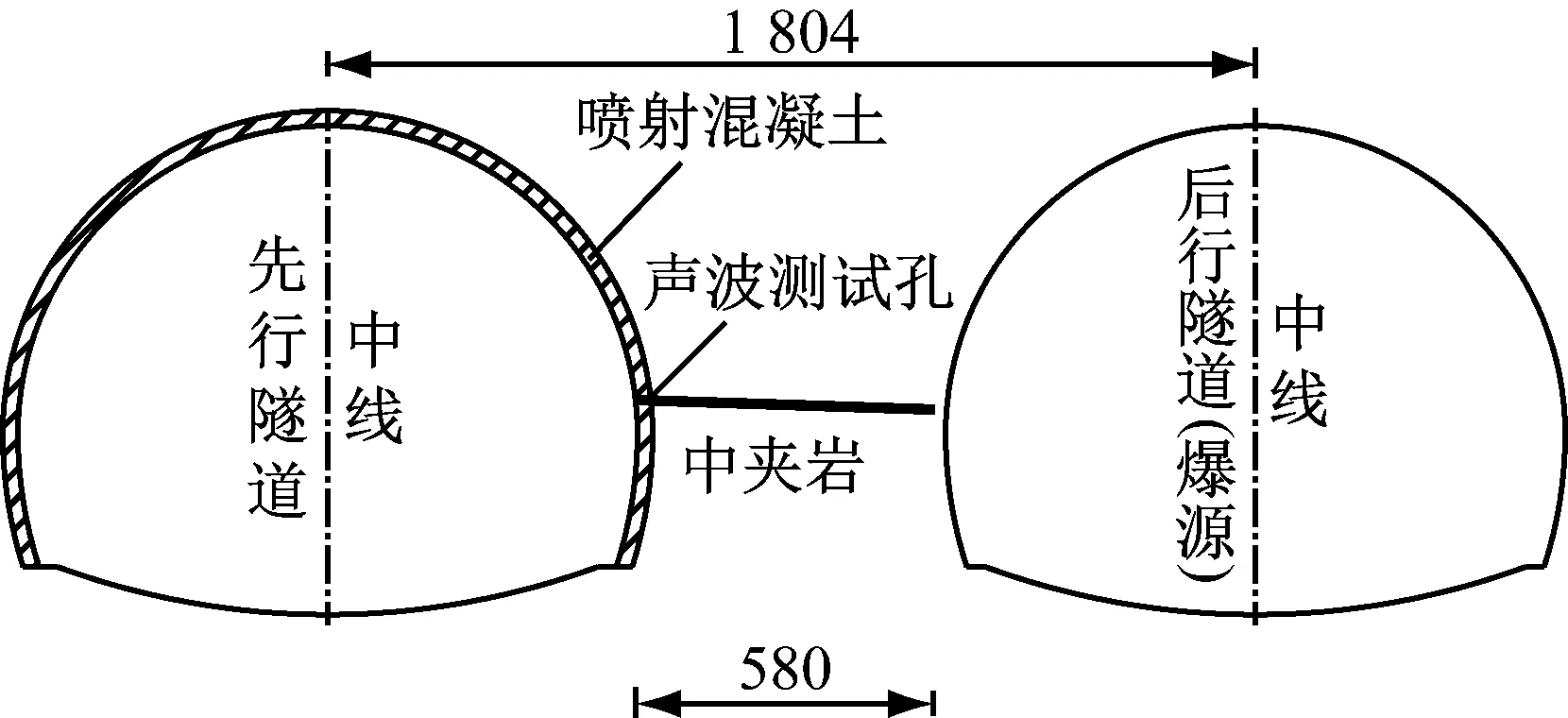
图10 声波测试孔布置图(cm)

声波测试方法采用单孔测试法，测孔深度为5.8 m，孔径为50 mm，靠近后行隧道侧中夹岩壁预留50 cm，移动步距0.2 m。考虑到传感器与孔壁的耦合作用，测孔均向下倾斜5°。本次声波测试共进行了4次，包括1次爆前声波测试和3次爆后声波测试，3次爆破开挖面的桩号分别为K11+392，K11+390，K11+388.5。声波测试仪器由RSM-SY5(T)声波检测仪和一发双收探头组成，图11为现场测试时的声波监测仪器。

(a) 钻孔(b) 声波检测仪(c) 一发双收探头

图11 现场测试时的声波监测仪器

Fig.11 Acoustic monitoring instrument for field test

工程中一般采用损伤变量D作为爆破损伤影响范围的判据，见式(8)，当声速降低率η>15%时，即认为岩体质量差[22]。此时岩体的损伤阈值Dcr为0.28，即当Dcr>0.28时，可判定开挖爆破对岩体产生损伤破坏。损伤阈值可用来判定爆破对围岩的影响深度。

(8)

式中：v0为爆前岩体的声波速度(m/s)；v为爆后对应v0测试部位岩体的声波速度(m/s)。

3.2 测试结果分析及验证

声波测孔爆破前后的波速与深度曲线，如图12所示。

图12 测孔爆破前后的波速与深度曲线

由图12可知，测孔深度为0.4～1.4 m，声波速度衰减率达42.6%，表明先行隧道爆破开挖对该段中夹岩体已经造成了破坏。孔深1.4～6.8 m，声波波速均>4 200 m/s，与文献[12]所测围岩波速基本吻合，表明该段围岩接近原岩，完整程度较好，损伤程度较低。随着后行隧道循环爆破次数的增加，孔深3.4～5.8 m，中夹岩体波速持续下降。表明该段中夹岩出现了的裂隙扩张，损伤程度不断加剧，对声波的传播造成了影响。3次爆破的声波波速平均降低率分别为4.37%，9.13%，11.97%。

为进一步反映不同爆破次数后中夹岩的累积损伤程度，由式(8)，得到测孔深度与损伤变量之间的关系，如图13所示。图13中的爆前、爆后岩体声波速度分别为后行隧道爆前和爆后岩体声波速度。

图13 测孔深度与损伤变量的关系

由图13可知，第1次爆破后，损伤变量小于0.28，表明岩体不会产生破坏。第2次爆破后，在测孔深度4.6 m处损伤变量大于临界值0.28，说明岩体已发生破坏，损伤范围为1.2 m。第3次爆破后，损伤变量持续上升，最大损伤变量达0.61。后行隧道中夹岩侧的损伤范围不断扩大，最大损伤范围2.2 m。而数值计算的最大损伤范围为2.4 m，与实测结果基本吻合，说明数值模拟的计算结果比较准确。

4 结 论

(1) 采用LS-DYNA有限元软件，基于HJC模型，引入损伤变量后，模拟了多循环推进式爆破对后行隧道围岩的累积损伤演化过程。计算结果表明，考虑累积损伤的计算值与实测值较吻合。后行隧道爆破振动对中夹岩侧拱肩和拱脚造成的损伤范围较大。

(2) 相比单次爆破荷载，考虑循环多次爆破荷载作用下中夹岩的最大损伤范围明显增加，而临界质点振速显著降低。因此，在评价爆破振动对中夹岩的稳定性时要考虑累积损伤效应的影响。

(3) 在多循环推进式爆破荷载条件下，装药量、最大损伤范围和临界损伤峰值质点振速之间具有良好的相关性，通过建立三者之间的函数关系，由单次爆破开挖的装药量，可以得到中夹岩的质点临界损伤振速。

(4) 从现场声波测试结果可知，后行隧道侧中夹岩的最大损伤范围与数值模拟计算得到的损伤范围基本吻合，表明本文所采用的爆破损伤数值模型和计算方法是可行的，对类似工程具有一定的参考价值。