基于Lighthill声类比理论的离心泵流动诱导噪声的数值模拟
司乔瑞, 盛国臣, 衡亚光, 崔强磊, 黄凯乐
(江苏大学 流体机械工程技术研究中心,江苏 镇江 212013)
离心泵广泛应用于国民经济各部门[1-3],由于其内部流动结构复杂,运行过程中常伴有强烈的噪声。随着制造加工精度的不断提高,离心泵的机械噪声逐渐得以控制,其流动诱导噪声日益成为主要的污染源[4]。流动诱导噪声的致声机理较为复杂,且在传播中极易与结构发生强耦合作用,引发泵体或管路的共振而产生新的辐射噪声;舰船用离心泵产生的流动诱导噪声经管路排出后,向水中直接辐射,成为船舶系统被识别的重要安全隐患。因此,对离心泵流动诱导噪声进行研究具有重要的学术价值和工程意义。
国内外对离心泵流动诱导噪声已进行了大量的研究,数值模拟技术是关注的重点。Lighthill[5-6]对流动致声问题提出开创性的声类比理论。Curle[7]在考虑静止固体边界影响的基础上,采用Kirchoff方法将Lighthill理论推广。Goldstein[8]研究了运动物体在流动介质内的发声问题,推导出广义Lighthill方程。1997年,Dong等[9]提出离心泵叶轮与隔舌间的相互作用是其内部流动噪声的一个重要来源,将其间隙加大到叶轮半径的20%左右后泵的振动噪声会明显降低。Langthjem等[10]提出了预测离心泵诱导噪声源的二维声学模型,并初步给出降低诱导噪声的水力设计准则。司乔瑞等[11]基于Lighthill声类比理论,提出基于CFD/CA(Computational Fluid Dymamics/Computational Acoustics; 计算流体力学+计算声学)的混合算法,在流场计算的基础上采用声学边界元法对离心泵声场进行了求解,并分析了声振耦合作用对声场分布的影响。该混合算法能满足工程实际的需要,但常用声学求解方法有统计能量法、声学边界元和声学有限元法,至今仍未有研究对各声学计算方法在离心泵流动诱导噪声计算方面的应用提出一些适用准则。
本文拟采用CFD/CA相结合的方法对IS65-50-165模型泵流动诱导噪声进行求解,比较声学边界元法和声学有限元法在计算时的优劣,探索离心泵流动诱导噪声规律,并提出离心泵流动诱导噪声模拟的相关适用准则。
1 求解理论
在流动声学问题中,流场和声场是统一的。非定常状态下,描述离心泵内部流场的基本控制方程组为N-S方程。
(1)

(2)

(3)
式中:eij为黏性应力张量;δij为Kronecker函数,i=j时,δij=1;i≠j时,δij=0。近场区域既是声源区也是声传播区,可用非线性方程组描述其流动过程。远场区域可视作声传播区域,声场可以用Helmholtz方程描述。离心泵流动诱导噪声的数值计算方法分为直接求解法和间接法两种。
直接法通过直接求解N-S方程组以获得流场与声场的物理解,但需要高精度的湍流模型和庞大的计算量,所以对于离心泵流动诱导噪声的直接求解还难以实现。间接法的理论基础是由N-S方程推导出的Lighthill声类比方程

(4)
(5)
式中:Tij是Lighthill应力张量;ρ为流体密度;ρ0为未受扰动时的流体密度;u为速度;p为流体受到的压强;p0为未受扰动时流体受到的压强;c0为声速;t为时间;x为空间坐标,指标i,j表示坐标轴方向分量,遵从张量中的求和约定,此方程适合无边界的自由空间。
随着CFD的快速发展,采用LES、DES和SST SAS等湍流模型进行流场计算已经能为声场计算提供相当准确的声源信息,基于CFD/CA的流动诱导噪声主要求解流程,如图1所示[12]。

图1 基于CFD/CA的离心泵流动噪声模拟流程图
2 数值计算
2.1 流场计算
文中选用模型泵设计参数如下:体积流量qVd=25 m3/h;扬程H=32 m;转速n=2 900 r/min;比转速ns=65.56;叶轮进口直径Dj=65 mm;叶轮出口直径D2=165 mm;叶片出口宽度b2=7 mm;叶片数Z=6。
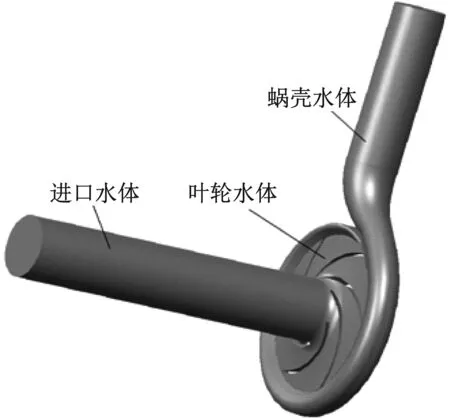
图2 计算域
模型泵计算域,如图2所示。包括:进口水体、叶轮水体、蜗壳水体。流体从进口流入叶轮,经过旋转做功后排入蜗壳,最终从蜗壳的出口流出。考虑进出口可能存在的回流现象,对进口水体和蜗壳水体出口部分进行了延长。
采用ICEM CFD 14.5专业网格生成器对计算域进行网格划分,并在蜗壳隔舌附近加大了网格密度。网格生成时需尽可能保证交界面两侧的网格节点数相同或相近,经过网格无关性分析后,最终采用的网格总数为:3 164 708个,其中进口水体、叶轮水体和蜗壳水体分别包含548 274个、1 488 384个和1 128 050个网格单元。计算模型泵的网格划分结果,如图3所示。

图3 网格化分
本文选取的SST SAS模型是近年来快速发展起来的一种URANS的改进模型,它基于SSTk-ω模型,同时兼具k-ω模型计算近壁区域黏性流动可靠性的特点。计算时进口边界取为速度进口,出口边界条件设置为出流,并按外特性试验值设置出流的参考压力。固壁表面设置为无滑移边界条件,并选取自动壁面函数,并按实际加工设置粗糙度为25 μm,湍流黏度项采用高精度的二阶格式,时间域上采用二阶全隐格式进行离散。时间步长设置为2.873 6×10-5s,即每个时间步长内叶轮旋转0.5°,总计算时间为0.42 s,对应叶轮旋转20圈。根据耐斯奎采样定理,流场计算可得到的有效分析频率为17 400 Hz。此外,考虑到节约计算机资源问题,选取并输出最后稳定的8圈计算结果,并保留声场计算所必须的速度、密度和压力三个变量作为声场时域信号[13]。
对压力脉动数据进行时域、频域分析可以从流场角度出发确定泵内主要噪声源的位置及频域特性,为声学分析奠定基础。当流场呈现出明显的周期性且这种周期性变化达到稳定状态之后,开始输出叶片及蜗壳表面的压力脉动时域信息,并保存叶轮旋转3个周期的数据文件作为后续声学计算的基础。定义压力系数Cp为[14]
(6)
式中:p为监测点的监测静压;pt为参考静压(101 325 Pa);u2为叶轮出口圆周速度。
离心泵内部流场的压力脉动可以采用强度分析及布置监测点的方法来衡量。在流场计算软件中,整数个叶轮旋转周期的平均压力系数可用式(7)表述
(7)
式中:x,y,z为监测点坐标;T为旋转周期数;N为旋转周期内的迭代步数。本章以最后三个旋转周期的计算结果做分析,所以T=3,N=2 160。衡量压力脉动强度的系数可以用式(8)所示的均方差表示,压力脉动强度系数大的地方说明压力脉动强度大,流体的非定常特性较强。截面及监测点布置,如图4所示。最终设计流量下模型泵蜗壳中截面及各断面压力脉动强度系数计算结果,如图5和图6所示。由此可知,叶轮出口中截面脉动强度最大,脉动强度分布在各截面并沿中截面对称,靠隔舌越近的截面脉动强度越大,反之则越小。
(8)

图4 截面及监测点布置图

图5 Qd下蜗壳中截面压力脉动强度系数分布
监测点A时域和频域分析结果,如图7所示。由图7(a)可知,设计工况下压力脉动波动小,而在小流量工况下波动大。从图7(b)可知:峰值主要集中在2 000 Hz以下的低频区,叶频(290 Hz)及其倍频是脉动的主要频率,且倍频呈现快速衰减趋势;各工况下,监测点叶频处的压力脉动幅值先随流量增大而减小,在设计流量下达到最小,随后随流量增加而增大。各工况下,压力脉动在轴频和叶频处的脉动幅值均远远大于其它频率成分,这说明在离心泵运转时,叶轮和隔舌间的动静干涉作用起重要作用。

截面I 截面II 截面V 截面VIII
图6Qd下各截面压力脉动强度系数分布
Fig.6 Intensity distribution of pressure pulsation at each volute section underQd

(a) 时域变化

(b) 频域特性
2.2 声场计算
2.2.1 基于CFD与声学边界元的离心泵流动诱导噪声计算
声场计算中的声源是由非定常流场计算决定的,离心泵流动诱导噪声最主要的声源类型为泵内部非定常流动激发的偶极子源。其主要集中在两个部分:①叶轮旋转使叶片与流体相互作用形成的旋转偶极子源,在LMS Virtual.Lab软件中也称为扇声源;②叶轮出流与蜗壳壁面干涉形成的偶极子源。采用结合CFD与声学边界元的计算流程,如图8所示。
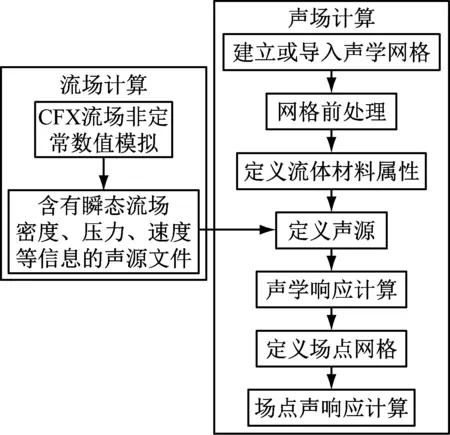
图8 基于CFD/BEM的计算流程图
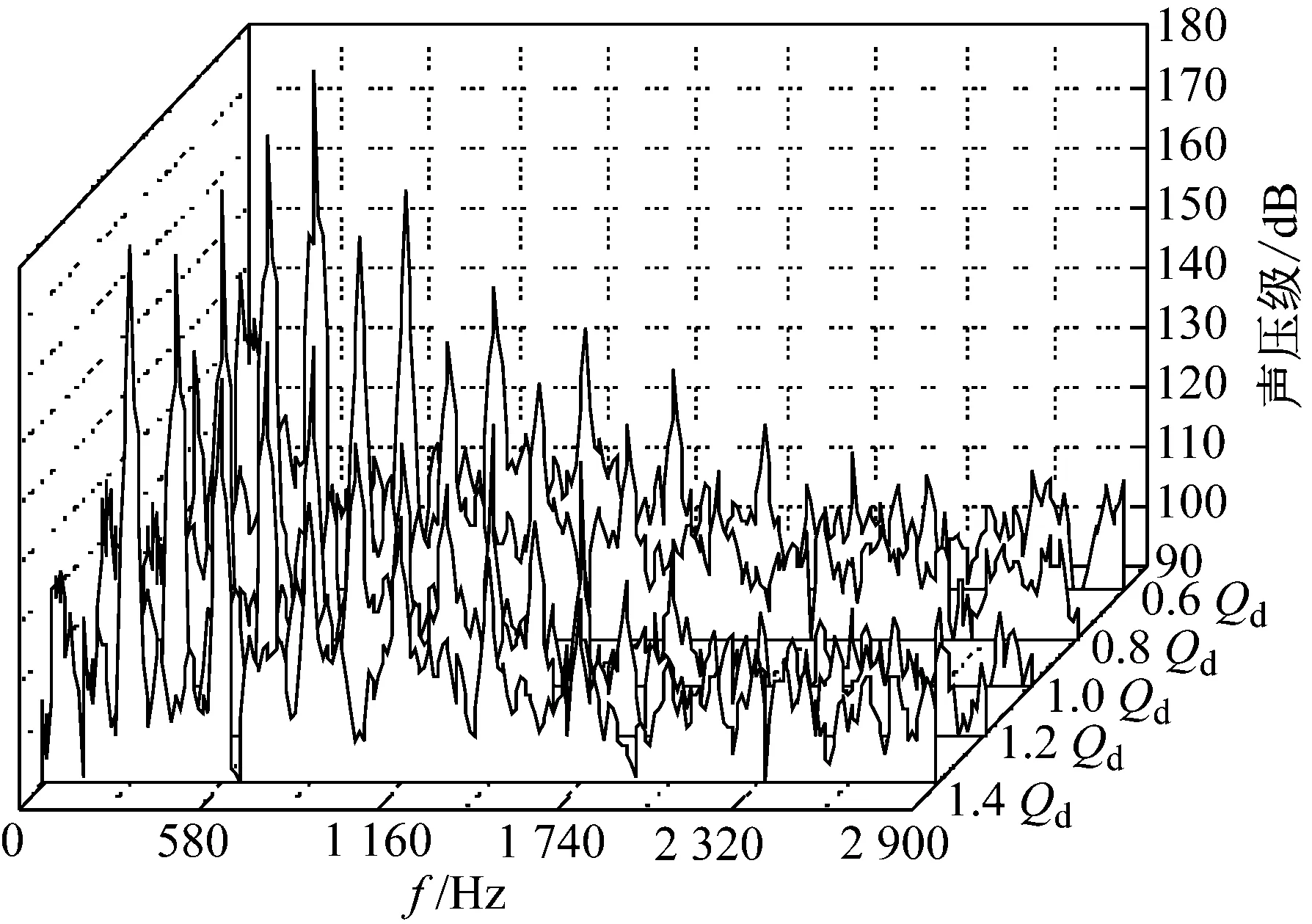
采用间接边界元法,定义蜗壳壁面为硬边界条件,进出口平面属性设置为全吸声,对于间接边界元模型需要的是面网格,而不是体网格。通常采用声学边界元方法计算,要求在最小波长内至少有6个网格单元,也就是最大单元的边长要小于最高计算频率处波长的1/6,即L 图9 模型泵声学边界元网格 定义完边界条件后,利用LMS Virtual.Lab软件提供的声学边界元求解器对模型泵内部声场进行求解。在进行泵内声场数值模拟前,沿叶轮出口圆周按螺旋线方向设置15个监测场点,如图4所示。监测场点总声压级在各流量下的分布结果,如图10所示,其中0°为隔舌起点位置。 图10 蜗壳监测点声压级分布图 由图10可知:在5种不同运行工况下,内声场皆显示出偶极子声源的声场特性,且在隔舌下游相邻监测点的声压级出现峰值;声压级在隔舌下游相邻监测点最大主要是因为该处的流道面积最小,叶轮出流受动、静干涉作用的影响最强,监测点距离蜗壳内壁面也最近;声压级随流量变化的结果与流动噪声测试规律一致,即小流量时较大,随着流量增大噪声减小,在1.0Qd~1.2Qd区间(高效区)呈现最低,当流量再进一步增大时噪声的声压级增大[15];叶轮出口监测点声压级分布不对称,大小不等值,再次证明了流动诱导噪声在离心泵内的产生与传播不但与叶轮出流相关,受蜗壳形状及叶轮和隔舌动静干涉作用的影响更大。 2.2.2 基于CFD与声学有限元的离心泵流动诱导噪声计算 声学有限元计算基于ACTRAN软件进行,该软件求解器具有限元法的共性,能够更好地与ANSYS CFX 14.5计算的流场结果联合。声源处理方面,ACTRAN提供的Lighthill声类比技术是基于式(4)所示的Lighthill方程的改进。从Lighthill方程出发,最终得到Lighthill声类比方程的有限元变分离散弱解形式,如式(9)所示 (9) 式中:右端第一源项为体声源,第二源项为面声源。从动量守恒方程可知面声源项在硬边界条件的刚性壁面上消失,在开口边界条件下,面声源项由自由场辐射取代,最终方程为[16] (10) 在基于CFD/CA的离心泵流动诱导噪声计算过程中,可以忽略计算域外边界的湍流非定常脉动,而蜗壳内表面的固壁计算域边界速度为零,因此,蜗壳流场形成的面声源项为零。由于离心泵内部湍流流场的雷诺数比较高,流场动能主要由大涡携带,因此,涡源项ρuiuj为主要声源。 对模型泵内部声场进行求解过程中,将叶轮及其上游的声源信息通过积分转换到蜗壳进口面作为面声源,蜗壳计算域本身则作为体声源载体进行计算,声场计算域及计算流程,如图11所示[17]。 ACTRAN软件对声源进行处理,为了减小截断误差,本文采用Hanning窗函数截取信号。划分声学网格时,需要蜗壳水体和经过延长后的出口管道体网格,保证每个波长内有4各节点即可。ACTRAN提供积分插值方法,如图12所示。相比广泛使用的线性插值法,这种方法能够在网格稀疏的条件下获得较好效果,并且不会造成声源信息的丢失,能够加快求解速度。 对面声源和体声源进行插值、设置声场计算边界条件及定义好场点网格后,使用ACTRAN提供的有限元声学求解器,选用二次插值法对流动声场进行计算。其中,出口场点的定义与前文边界元声场计算时出口场点的坐标相同。 叶频(290 Hz)下,各工况的声场声压级分布对比,如图13所示。由图13可知:5种工况下,最大声压级均出现在隔舌附近处,表明隔舌处是较重要的噪声源;与图10展示的一样,隔舌附近明显存在低声压级的区域,这是由于叶轮出流冲击隔舌后在隔舌壁面形成边界层,尤其是非设计流量下沿螺旋线方向会存在一定的分离区[18-19],此处流体间的相互作用小,在声学上呈现低压区;叶轮出口还存在多个低噪区,表明叶轮出口的流动结构会造成流动声源分布的不均匀;最大声压级的变化规律与声学边界元法得出的结果一致。 (a) 计算域 (b) 求解流程图 (a) 积分插值(b) 线性插值 图12 声源插值方法 Fig.12 Interpolation method of noise source 对声场计算的频域结果进行提取以得到出口场点上的声学信息,经过数据传递后可得5种流量下出口场点A2的声压级频域分布,如图14所示。由图14可知,基于CFD和声学有限元方法求解的出口场点声压级曲线是具有明显离散性的宽频谱,叶频及其倍频是其主频,轴频及其倍频也是离散点,叶频下声压级最大;0.6Qd和1.4Qd下,响应曲线在低频具有更多的分量;由声压级频域响应曲线可以看出,声学有限元法在湍流噪声的预估方面把握得较好。 (c) 1.0 Qd(d) 1.2 Qd(e) 1.4 Qd 图13 叶频下各工况的声场声压级分布 Fig.13 Sound pressure level distribution of impeller passing frequency at several flow rates 图14 A2声压级频域响应曲线 为了验证文中算法的正确性,搭建了离心泵流动诱导噪声测试试验台,试验台实景图如图15(a)所示。离心泵流动诱导噪声测试系统由水循环采集系统和数据采集系统两部分组成,其系统结构如图15(b)所示,水循环系统提供必需的运行环境,数据采集系统利用传感器对不同工况下测得的物理量进行采集和处理分析。出口第一个水听器安装的位置也即是采用声学边界元和声学有限元方法进行声场计算时场点设置的位置。 (a)试验台 (b)系统结构图 分别将采用BEM和FEM计算得到的叶频下蜗壳出口场点声压级与试验数据进行对比,结果如图16所示。由图16可知,采用BEM和FEM两种方法得到的声学模拟结果均与试验数据趋势一致,出口场点叶频下声压级先减小,在1.2Qd达到最小,然后增大;采用BEM方法得到的最大误差数值<5.3 dB,采用FEM方法得到的最大误差数值<3.2 dB,这说明两种模拟结果均可信;考虑计算资源及时间,非定常特性不强工况下,选用BEM较合理;非定常特性较强的工况,选用FEM虽然建模更加复杂,计算时间变长,但计算结果与实际更加吻合,对内流场宽频噪声问题的研究更占优势。 图16 290 Hz下各工况叶频声压级试验和模拟值 Fig.16 Simulation and experimental results of sound pressure level at impeller passing frequency under several flow rates (1) 流场计算的结果表明:SST SAS模拟既能较准确地提供声源信息,又能避免LES或DES模拟对网格及计算资源的高要求;压力脉动的模拟和试验结果表明:蜗壳隔舌附近压力脉动强度最大,叶片通过频率及其倍频是各监测点上压力脉动的主频,仅仅判断比较声学性能,只需比较分析叶频下声压级即可。叶轮与隔舌间的动静干涉作用是离心泵流动诱导噪声的主要原因。 (2) 离心泵流动诱导噪声呈现偶极子特性,总声压级随流量的增加先减小,在最高效率点附近最小,随后随流量的增加变大。 (3) 基于CFD/CA的数值计算方法可以用于离心泵流动诱导噪声的预测;声学边界元法能快速有效地计算出叶频及其倍频噪声的大小,声学有限元法则在计算远场流动噪声时克服了积分方法不能求解复杂边界格林函数的缺点,虽然建模更加复杂,计算时间变长,但计算结果与实际更加吻合,对内流场宽频噪声问题的研究更适用。





3 试验验证
3.1 试验系统


3.2 试验结果

4 结 论

