基于波分析法的L型结构弯-扭耦合振动研究

沈轻舟， 车驰东

(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室 高新船舶与深海开发装备协同创新中心，上海 200240)

结构声在典型船舶结构中的传递规律对船舶声学设计以及减振降噪有着重要的指导作用。近年来，随着计算机技术及软件的发展，有限元法(Finite Element Method，FEM)、统计能量分析(Statistic Energy Analysis，SEA)以及边界元(Boundary Element Method，BEM)逐步成为声学计算的主要手段。刘延善等[1]将无网格FEM-BEM应用在舱室空间低频声场计算中并取得了较高的精度；邹春平等[2]结合有限元法与模态综合法对高频下大型船舶结构进行了振动分析，并实现了较小的计算资源对大型结构振动的准确预报；温华兵等[3]使用FE-SEA 混合法验证了空心阻振质量的减振效果。但是，SEA对模态密度的要求使得其在低频下有较大误差，而FEM和BEM对网格尺寸及边界条件的敏感也使得其计算量与误差随着频率指数上升。另一方面，数值计算通常只计算结构声场与能量分布，不能直接对结构声传递进行参数分析，因此在传递机理上，使用波分析法等解析方法更为有效。

Cremer等[4]在其著作《Structure-Borne Sound》中指出，结构振动可以看作沿不同方向传递的不同类型结构波的互相叠加，且结构波在传递过程中遇到任何阻抗突变都会发生反射与透射，同时伴随波形转换。国内外学者在此基础上展开了大量研究。

Kessissoglou[5]研究了外激励下L型板内的能量传递随频率的变化关系，在忽略平面内振动情况下得到能量透射系数随着频率与传递距离的上升而上升的结果； Grice等[6-7]则针对船舶典型结构，利用波分析法建立了以梁为框架、将板单元等效为阻抗的模型并进行了有限元验算，理论结果和实验数据极高的一致性证明了将板单元等效为阻抗的可行性；姚熊亮等[8]分析了弯曲波在各类组合板结构中的传递规律，并给出了不同结构、不同参数下的隔声量公式，并深入研究了偏心阻振质量在船体板上的阻振机理与隔声特性，结果表明偏心阻振质量有效抑制了声辐射[9]；车驰东等[10]改变转角处的角度与阻振质量对弯曲波的传递规律进行参数分析，得到了较好的阻振效果；Dijckmans[11]使用波分析法计算了SEA法在不同侧墙节点处的耦合损失因子，并据此对不同结构的隔声效果进行了分析。

综合各类研究文献可见，前人的研究主要集中与弯曲波与纵波的耦合上，对扭转波的涉及相对较少。当弯曲波入射到垂直直角时，会诱发透射与反射纵波；当其入射至水平转角时，诱发的则是扭转波；后者在同一层甲板内的管路振动中更加常见。另一方面，无限结构基本不形成驻波，不涉及模态问题，与实际结构相差甚远，而有限结构主要考虑模态响应问题与振动能量分布，两者存在一定差异，且研究两者相互关系的文献较少。基于上述原因，本文将研究弯曲波入射诱发扭转波情况下的能量传递规律，并使用半无限长结构的传递系数去预报有限结构的声场。

1 理论分析

1.1 半无限长结构分析

首先考虑两根半无限长均质梁构成的L型转角结构。以转角连接点为原点，分别在两根梁上建立局部坐标系X1OY1，X2OY2，如图1所示。

图1 L型梁结构示意图(弯曲波入射)Fig.1 L-shaped structure(bending wave impinging)

根据Cremer等的研究，入射波沿x1传递至转角处时，会激发反射波、透射波与近场波，并伴随有波形转换； 而对于某一激励频率ω，单位振幅弯曲波的位移表达式可表示为

(1)

式中:kb为该频率下的弯曲波波数。

因此，两梁中的合成振动位移表达式可表示为

(1) 单位振幅弯曲波入射

(2)

(3)

(4)

(5)

(2) 单位振幅扭转波入射

(6)

(7)

(8)

(9)

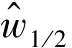
而转角处边界条件为

(1) 位移连续

(10)

(11)

(12)

(2) 力与力矩平衡

(13)

(14)

(15)

结合本构关系， 将位移表达式(2)～式(5)、式(6)～式(9)分别代入边界条件式(10)～式(15)中，可以得到弯曲波、扭转波入射下，透反射系数的方程；将该方程无量纲化后，即可得到式(16)和式(17)

(16)

(17)

透反射系数通常为复数，为进一步研究结构声能量传递之间的关系，可将其转化为能量传递效率，如下所示:

(1) 弯曲波入射

弯曲波-弯曲波能量反射系数

(18)

弯曲波-弯曲波能量透射系数

(19)

弯曲波-扭转波能量反射系数

(20)

弯曲波-扭转波能量透射系数

(21)

(2) 扭转波入射

扭转波-弯曲波能量反射系数

(22)

扭转波-弯曲波能量透射系数

(23)

扭转波-扭转波能量反射系数

(24)

扭转波-扭转波能量透射系数

(25)

式中:Zb为梁的弯曲波特征阻抗，其表达式为Zb=m′·cb；Zt为梁的扭转波特征阻抗， 其表达式为Zt=J′·ct；m′与J′分别为单位长度的质量与惯量。

而根据能量守恒定理，在无阻尼时很显然有

(1) 弯曲波入射

ρBB+τBB+ρBT+τBT=1

(26)

(2) 扭转波入射

ρTB+τTB+ρTT+τTT=1

(27)

1.2 有限长结构分析

现通过上述半无限长的传递系数预报有限结构声场。设构成转角的两根梁分别长l1,l2，且两梁端部反射系数为rB1,rB2,rT1,rT2(假设端部无波形转换)。

对于有限结构，外激励引起的入射波会在末端及转角间不断传递，因此沿某方向传递的结构声是一系列反射波和透射波的级数，而系统的振动分布则等价于沿不同方向传递的波的矢量叠加；而对于一维简直梁，即为沿x正方向的正行波及沿x负方向的逆行波以及近场波的组合，因此构成转角梁结构的位移表达式为

(28)

(29)

(30)

(31)

式中:B为弯曲波振幅；T为扭转波振幅； 上标+为该波正行； 上标-为该波逆行； 下标1/2为梁1/2； 上标j为近场波。

正逆行波的振幅可结合各节点处的边界条件建立平衡方程解得；而由无量纲反射/透射系数的定义可知，这些正逆行波的振幅也可在节点处与无限结构的反射/透射系数建立平衡方程解得，且相比于直接解析，其形式更加简单，物理关系更加明确。其方程组如下所示

(1) 梁1端部

(32)

(33)

(34)

(2) 梁2端部

(35)

(36)

(37)

(3) 转角处

(38)

(39)

(40)

(41)

(42)

(43)

结合梁2外端、梁1梁2连接处的平衡方程，最终可以得到控制方程为

[D]·{A}={F}

(44)

式中： {A}为各波波动响应向量； [D]为波动刚度矩阵，它们的形式见附录； {F}为外激励项。

(1) 强迫振动下的结构声场

当有外激励源时， {C}的表达式如式(45)所示

(45)

(2) 自由振动下的固有频率

系统作自由振动时，外激励项{F}的值为0，因此上式变为齐次方程

[D]·{A}={0}

(46)

在固有频率下波动响应向量{A}有非零解，而其充要条件为波动刚度矩阵[M]的值为0，故固有频率的解可等效为式(47)的解

|D|=0

(47)

这和通过解析法联立边界条件解得固有频率是等效的。

2 数值计算

为研究无限结构中的能量传递规律，现利用数值方法模拟能量在半无限结构中的传递规律。设试验结构为一半无限长L型304不锈钢方管，其截面尺寸为20×20×0.8 mm，考虑到Euler-Bernoulli梁的理论假设限制[12]

(48)

故该结构计算的频域限制在10 000 Hz以下。数值计算结果如图2和图3所示。

图2 能量透射与反射效率(弯曲波入射)Fig.2 Energy efficiency(bending wave impinging)

图3 能量透射与反射效率(扭转波入射)Fig.3 Energy efficiency(torsional wave impinging)

由图2和图3可得出如下结论:

(1) 计算频域内所有能量系数加起来等于1，说明计算结果符合能量守恒定律；

(2) 弯曲波入射时，低频能量转换形式以弯曲波的互相反射与透射为主，高频部分主要为弯曲波至扭转波，总弯曲波能量随频率上升而下降；

(3) 扭转波入射时，低频能量转换形式集中为扭转波反射为扭转波，高频能量偏向于扭转波透射为弯曲波，总弯曲波能量随频率上升而上升；

(4) 在计算频域内，两种工况均出现总反射能量随频率上升而下降、总透射能量随频率上升而上升的趋势。

能量传递系数除了随频率变化外，还受到梁的物性参数的影响；梁之间不同的刚度、密度均会使得传递系数发生偏移。考虑到结构二次声辐射主要源自弯曲波，故仅对梁12不同密度、刚度比下的ρBB，τBB进行计算。工况1为参照组，两梁材料均为304不锈钢，其他工况改变了梁2的密度、刚度，如表1所示(表中的刚度、密度比表征梁1与梁2参数之比)。

表1 不同工况的结构参数Tab.1 Parameters of different condition

计算结果如图4、图5所示，其展示了弯曲波-弯曲波能量反射、透射系数在上述条件下的变化:

(1) 弯曲波-弯曲波能量反射系数随着梁12的密度比、刚度比的增加呈上升趋势；

(2) 弯曲波-弯曲波能量透射系数则随着梁12的密度比、刚度比的降低呈下降趋势，但是在高频下(尤其是密度比)对系数的影响逐渐减少。

图4 能量系数-密度比曲线Fig.4 Energy efficiency-density ratio

图5 能量系数-刚度比曲线Fig.5 Energy efficiency-stiffness ratio

3 实 验

为验证利用无限结构透反射系数求解有限结构声场的可行性，现利用一简化的转角结构进行实验。

测试对象是由两根20×20×0.8 mm的方管构成的L形转角结构，一端固定在基座上，另一端自由。信号发生器产生正弦信号并通过电磁激振器作用于自由端以提供入射波；激振头与自由端连接处安装有力传感器用以换算入射波幅值。

被测结构上布置有7个测点，每根梁4个(第4个测点两梁共用，如图6所示)，安装于测点上的加速度传感器记录正弦激励下的稳态响应，并根据数据计算出正逆行波与近场波分量。需要说明的是，由于安装原因，测点1距外端15 mm，测点4朝梁1侧偏10 mm，测点7距固定端82 mm；测点2～测点7布置于梁的上方，而测点1由于上方已有激振器，为测量激振点的加速度只能布置于梁下方，其相位差与一般测点差180°。

出于规避不稳定因素与提高信噪比的考虑，实测激励分为宽频激励和单频激励两种，宽频激励为30～1 000 Hz的正弦扫频信号激励以识别系统的固有频率；单频信号为若干频率的正弦信号激励(31.5 Hz，50 Hz，63 Hz，100 Hz，125 Hz，200 Hz，250 Hz，400 Hz，500 Hz，600 Hz，800 Hz，1 000 Hz)，并得到各频率下的加速度及速度响应。

根据波动方程，弯曲波有4个分量(正逆行波、正逆近场波幅值)，因此4个测点数据就可以解出弯曲波的各波幅值，进而得到对应的振型。

理论分析了假设固定端和自由端为理想边界，但实际工程中固定端必然是一个大阻抗边界，并且安装了激振器的自由端也带有一定的阻抗，导致本实验中难以忽略其对边界反射系数的影响。由于已得到反射与透射波幅分量，结合边界反射系数的定义

(49)

可以直接用实验数据修正阻抗边界的影响，因此对数值计算中的边界进行了修正以方便和实测值进行比较。

(1) 不同频率下的振型分布(见图7～图9)。

图6 实验模型几何尺寸与测点布置位置(单位: mm)Fig.6 Test object and sensor placement(unit: mm)

图7 100 Hz下数值解(理论/理论修正)与实验弯曲波场对比Fig.7 Acoustic field compare among numerical result and experiment under 100 Hz

图8 250 Hz下数值解(理论/理论修正)与实验弯曲波场对比Fig.8 Acoustic field compare among numerical result and experiment under 250 Hz

图9 400 Hz下数值解(理论/理论修正)与实验弯曲波场对比Fig.9 Acoustic field compare among numerical result and experiment under 400 Hz

图7～图9是不同频率下梁1、梁2的振型图，三根曲线分别代表实验值、理想数值解、经过反射系数修正(阻抗边界)的数值解。比较以上图片可以得到以下结论:

①边界阻抗会显著地影响结构声场，梁1、梁2的阻抗边界数值解均较理想边界数值解更接近实验值，在相位上尤其明显，因此有限结构声场预测中应当测量边界传递系数以修正模型；

②梁1的数值解在激振端的幅值上与实验值存在明显误差，通过比较可以看出梁1激振端的近场波明显高于理论解，这可能是激励端的传感器附加质量较大导致，在这种情况下需要对激励端的近场波幅值进行进一步修正。

(2) 同一测点振幅随频率的变化(图10)。

图10反映了扫频下测点2、测点6的振幅随频率的变化，虚线代表阻抗边界数值解的频率关系，实线是实验值的频率关系。计算结果表明阻抗边界数值解的趋势与实验值的趋势基本相同，利用带阻抗边界修正的半无限传递系数模型可以预报有限结构声场。

图10 两梁测点振幅-频率趋势图Fig.10 Amplitude-frequency trend diagram at the measure points

4 结 论

在波分析法的基础上，研究了结构波在弯-扭耦合振动问题中的传递规律，并基于此提出一种基于半无限长结构传递系数的有限结构声场预报方法，通过实验测量值与理论解的对比可以得到以下结论:

(1) 在工程应用的频域下，可认为结构波在弯-扭耦合振动中的传递存在规律——随频率上升，总反射能量下降而透射能量上升；同时波形转换的趋势也随频率上升而上升。

(2) 使用无限传递系数预报有限结构声场是可行的，但边界阻抗会显著地影响预报结果，而通过修正结构波在边界的传递系数则可有效地提高该方法的准确度。

附录：

[D]为12×12波动刚度矩阵，考虑到近场波不参与能量传递，故忽略近场波后得到的8×8矩阵为

{A}为各波波动响应向量