基于MARKOV切换拓扑通信策略的自主车队控制

吴利刚，乔 栋，周 倩

(1.山西大同大学机电工程学院，山西大同037003；2.山西大同大学建筑与测绘工程学院，山西大同037003；3.山西大同大学商学院，山西大同037009)

随着城市化进程的快速发展，道路拥挤问题已成为中国各大城市面临的主要交通问题，每年由交通拥挤、交通事故及环境污染所造成的损失耗资达数十亿美元。仅仅通过增加道路面积来提升道路的通行能力，是指标不治本的。通过智能交通系统中的自主车队控制（控制车辆以队列的形式自主安全行驶）来增加交通流量，减少交通事故是首选方法[1-3]。

关于自主车队的控制研究已经取得大量的成果[4-5]，但现有的研究大多忽视了以下两个方面：（1）在已有的研究成果中，大多是基于领头车-前车通信策略的前提，对车辆的网络受限进行研究的，这在实际中是难以应用的；（2）车辆间通讯问题不仅仅是只于前车或领头车有关系，应考虑整个车队间的车辆通信，来最大限度的增大道路的通行能力。

针对上述两个问题，本文采用动态的通讯策略，且车辆间的网络通讯策略的切换可用Markov过程描述，并将自主车队控制系统建模为Markovian跳变系统，并为跟随车辆设计了分布式切换控制器。

1 车队建模和基础知识

1.1 图论

车辆间的相互关系，可以用有向图G(υ,ε,Λ)建模，顶点υ∈{υ1,…,υN}代表N辆车组成的集合，边ε⊆υ×υ表示车辆间通讯关系的集合，Λ=[aij]表示权重连接矩阵。例如，(υi,υj)∈ε，aij＞0表示车辆i可以接收到车辆j的状态信息；否则(υi,υj)∉ε和aij=0。对于网络化自主控制车队，aii=0成立。边(υi,υj)中，υj表示头节点，υi表示尾节点。对于一个边序列 (υi,υk)，(υk,υl)，…，(υm,υj)称为从车辆i到车辆j的一条有向路径。如果根节点(只有子节点，没有父节点)到其他节点都有一条有向路径，则称这个图具有一个有向生成树，也就是说领头车的状态信息通过一条有向的通信路径传送到跟随车辆。υi的邻节点可用Ni=(υj∈υ：(υi,υj)∈ε)表示，节点υi的入度表示为，入度矩阵为Δ=diag{d1,…dN}，拉普拉斯矩阵为L=Δ-ΛT。相应的出度为，出度矩阵为，拉普拉斯列矩阵Lo=Δo-ΛT。如果某节点的入度等于出度，则这个点是平衡的。当且仅当有向图含有一个有向生产树，则0是La⁃placian矩阵L的单一特征值，其它特征值都具有正实部。矩阵L的重要特征值是每行元素的和为0，所以1是0特征值所对应的特征向量。

1.2 Markov切换拓扑

在每个采样瞬时k，车辆间的通讯关系可用有向生成树表示，每一个节点代表每一辆车，而车辆间的通讯关系用边来表示。本文采用的通信拓扑是不确定的，而且是随机切换的。假设切换拓扑通过一个图的集合而且切换信号用{θ(k),k∈N+}表示。这里，假设{θ(k),k∈N+}是一个有限集合的 Markov链，θ(k)∈S={1,…,q}，转移概率Pr o{θ(k+1)=v|θ(k)=l}=πlv，且 Pr o(θ(k)=l)=πl(k)。这里 Pr o(θ(0)=l)=π0l，π0l是图Gl，∀l∈S的初始概率。Π0=[π01,…,π0q]T是初始概率分布。πl(k)是图Gl在k时刻的转移概率，Π(k)=[π1(k),…,πq(k)]T是拓扑模式在k时刻的转移概率。πlv是从模式l到模式v的但不转移概率，且，∀l∈S。 π=[πlv]q×q是转移概率矩阵。因此，Π(k+1)=πTΠ(k)成立。矩阵 Λ(θ(k))的邻接矩阵和图G(θ(k))的拉普拉斯矩阵分别定义为Λ(θ(k)) ∈{Λ1,Λ2,…Λq} 和L(θ(k)) ∈{L1,L2,…Lq} 。

注1：由于θ(k)∈S={1,…,q}是一个有限状态的Markov链，平稳分布总是存在的。而且，对于Mar⁃kov链至少存在一个正回归闭集。由于每一个拓扑都含有一个有向生成树，因此Markov链是不需要遍历的，则要求Markov链是遍历的。对于遍历性的放宽，使得本文对于切换拓扑的使用更具实用性。

1.3 奇异系统的基本概念

对于奇异系统Ex(k+1)=Ax(k)，令E，A∈Rn×n，则

定义1：当∀s∈C，det(sE-A)≠0时，则矩阵束(E,A)是正则的；

定义2：对于任意的∀s∈C，并且 deg(d et(sE-A))=rank(E)成立时，则矩阵束(E,A)是因果的。

定义3：如果矩阵束(E,A)是正则的、因果的且渐近稳定的，则(E,A)是可接受的。

引理1：矩阵束(E,A)是可接受的，当且仅当存在矩阵P∈Rn×n满足ETPE≥0和ATPA-ETPE＜0。

1.4 车队建模

对于网络化车队控制系统，奇异的跟随车辆动态模型为：

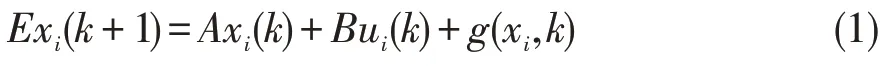
其中，i=1,2,…,N，xi(k)∈Rn和ui(k)∈Rm是车辆i的状态向量与控制输入，g(xi,k)∈Rn×n是连续的非线性项，A∈Rn×n和B∈Rn×m为定常矩阵，E∈Rn×n，且rank(E)=r＜n，xi(0)是系统的初始状态。

假设 1：如果存在矩阵M∈Rn×n，对于x，y∈Rn，不等式

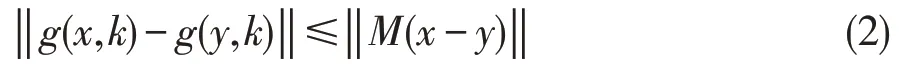
成立，则g(x,k)满足Lipschitz条件。

假设2：系统(1)是Y-可控的，当且仅当

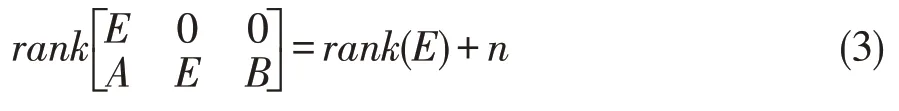
成立。

本文的目标是为跟随车辆设计设计如下形式的控制律

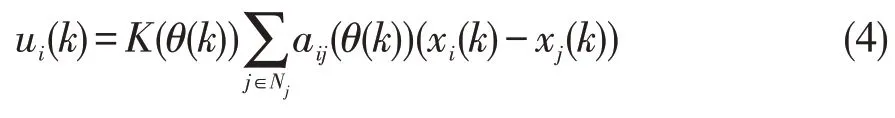
达到期望的车间距误差。其中K(θ(k))是需要设计的控制器增益矩阵。

定义4：网络化自主车队控制系统，在任意初始状态xi(0)和控制律(4)的作用下，且车辆间通讯的Markov切换拓扑满足集合，能够达到均方一致性(AMS-consensus)和正则和因果的，当且仅当对于i，j=1,2,…,N，

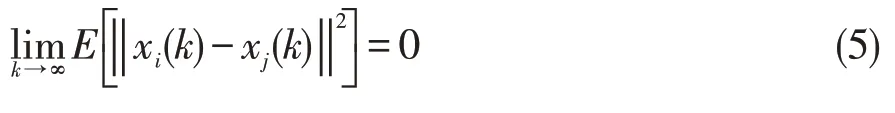
成立。

2 稳定性分析及控制器设计

问题1：对于切换Markov通讯策略的网络化自主车队控制系统，设计控制器律(4)使得车队控制系统达到AMS-consensus。

通过求解问题1，本文首先获得网络化自主车队控制系统（1）AMS-consensus稳定的一个充分条件。基于上述条件，给出了控制器设计算法。

令Ik={x(t),θ(t),t=0,1,2,…k}，则车队控制系统(1)在控制律(4)作用下的闭环系统为：

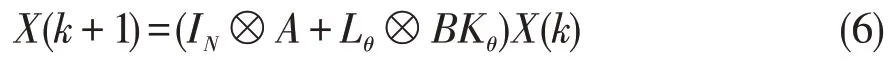
通过下面的引理2，可以获得本文的主要结果。

引理2：给定矩阵

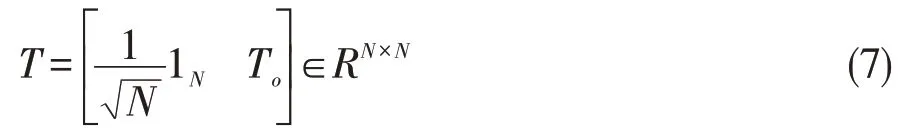
其中，T0是IN的正交补矩阵且满足=I。类似的变换，对于有向图的拉普拉斯oN-1矩阵L∈RN×N、矩阵L0和矩阵LTL有

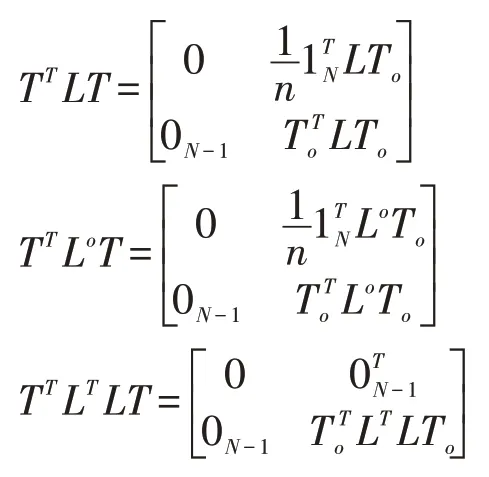
根据引理2，可以用如下的关系进行状态变量之间的转换。

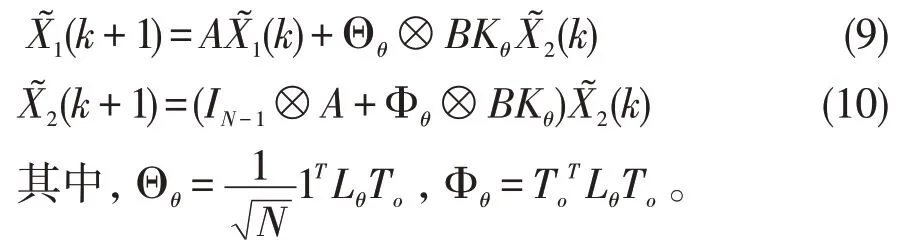
通过引理2，很容易获得矩阵T是正交矩阵，而且通过矩阵理论的相关知识可知，矩阵的正交变换并不改变其范数。基于上述的讨论，为了将系统(6)的一致性问题转换为系统(9)和(10)的稳定性问题，需要下述的定义。

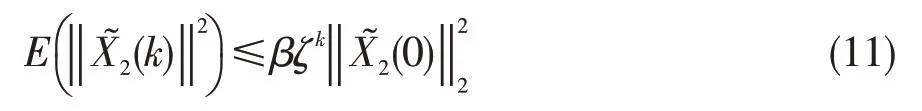
成立，对于k=0,1,…，任意的X˜2(0)和β≥1，0＜ζ＜1。

本文的主要结果如下。

定理1：对于网络化自主车队控制系统(1)在控制律(4)的作用下，且通信策略满足Markovian切换拓扑，达到均方稳定，当且仅当存在矩阵Pl＞0、Pl∈R(N-1)n×(N-1)n、Q＞0、R＞0和l∈S，使得

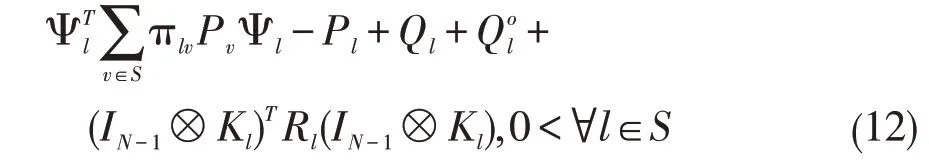
证明：为了证明系统(9)和(10)的稳定性，定义随机Lyapunov函数：

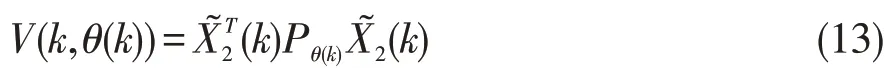
其中，θ(k)∈S={1,…,q}。

令θ(k)=l，θ(k+1)=v和l,v∈S，可得

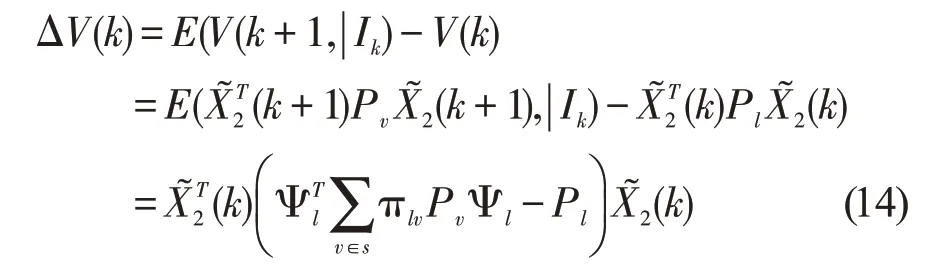
其中，Ψl=IN-1⊗A+Φl⊗BKl。

如果(12)成立，可得

通过(14)和(15)，可以获得：

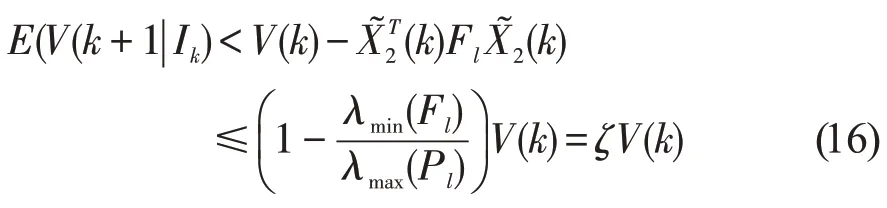
从而λmax(Fl)＜λmax(Pl)和0＜ζ＜1成立。

同理，为了获得定义5的均方稳定性条件，可得等式：

根据条件均值平滑特性的概念，通过(17)可得

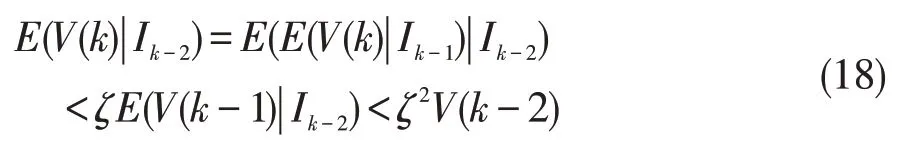
通过递归(16)、(17)和(18)，可得

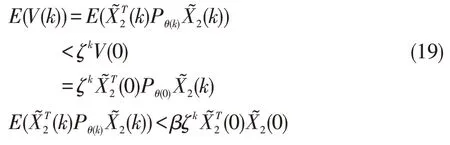
其中，β=λmax(Pθ(0))/λmin(Pθ(0))＞1和0＜ζ＜1。

通过定义5可知，系统(9)和(10)指数均方稳定，所以网络化自主车队控制系统(1)在控制律(4)的作用下，且通信策略满足Markovian切换拓扑，达到均方稳定。

下面给出了控制律(4)的设计方法，通过定理1和舒尔补定理可以获得随机控制器增益存在的充分条件。

定理2：对于网络化自主车队控制系统(1)在控制律(4)的作用下，且通信策略满足Markovian切换拓扑，达到均方稳定，当且仅当存在矩阵正定Pl、Ml∈R(N-1)n×(N-1)n满足线性矩阵不等式

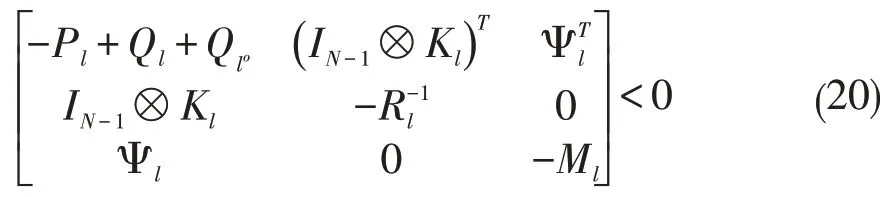
对于定理2的条件中存在许多矩阵的求逆约束，不能直接的应用标准的线性矩阵不等式求解方法，可以通过锥互补线性的方法来求解不等式(20)和以下的控制算法。

MS-consensus算法：

步骤1：对于所有的l∈S，寻找可行集合满足不等式(20)，否则退出。

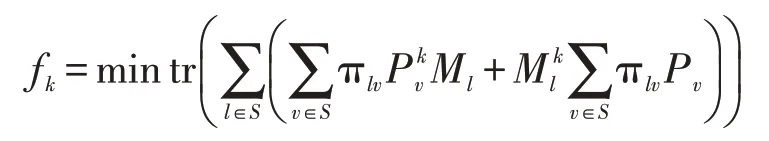
步骤3：如果‖fk-fk-1‖＜δ成立，且δ设定的惩罚参数，可以获得可行解K1，并且退出算法。否则，设置k=k+1，更新返回到步骤2。

注2：在实际应用中，本小节所提出的协同式控制算法，相比文献[6]，降低了对系统的动态模型和通讯拓扑的要求，所获得结果实用性更强。

3 仿真实验

通过MATLAB仿真软件，使用Simulink搭建了由4辆车所组成的网络化自主车队控制系统，并将本文所提出的控制算法应用到所搭建的模型中。

车辆的基本参数设置参照文献[5]。车辆间通讯信息的传输可用三个有向图={G1,G2,G3}表示，且每个有向图代表了一个生产树，见图1。

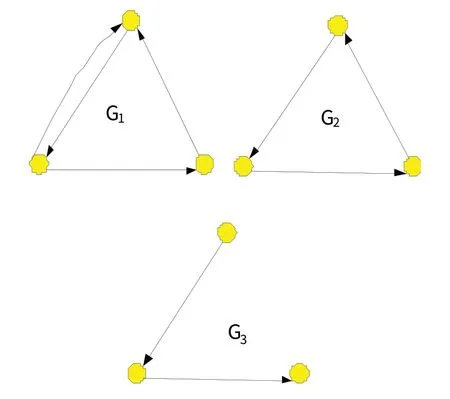
图1 有向图集合

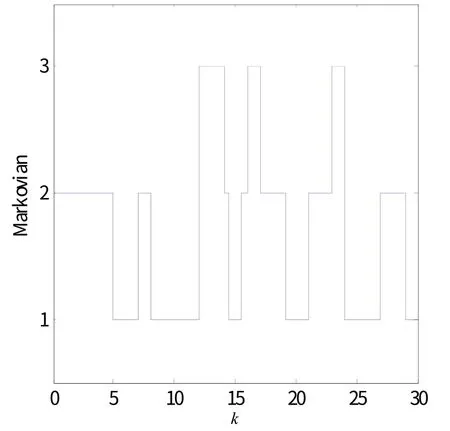
图2 切换的马尔科夫通讯拓扑序列

通过MS-consensus算法，可以获得控制器增益：

K1=[-0.1272 -0.5001]

K2=[-0.1241 -0.4878]

K3=[-0.1088 -0.4281]

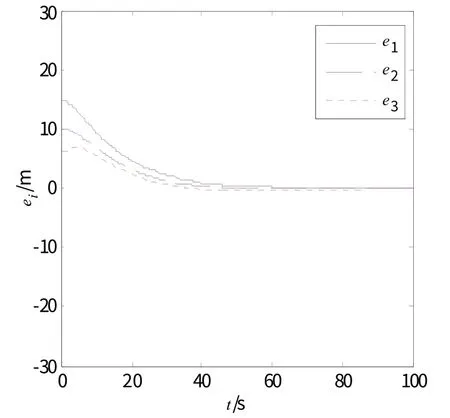
图3 相邻车辆的车间距误差

从仿真图3可以看出，通过本章所设计的控制器，基于动态Markov切换拓扑网络通信的自主车队控制系统，4辆跟随车辆能够与其直接前车达到期望的车间距。

4 结语

网络化自主车队中关于车辆状态信息的交换问题，车辆间网络通信不再是简单的前车或者领头车通信策略，而且可以用动态的Markov切换拓扑进行描述。