一种导弹模型气动特性的数值分析*

纪 录,吴国东,王志军,刘亚昆,徐永杰

(中北大学机电工程学院,太原 030051)

0 引言

导弹是依靠自身动力装置推进,由制导系统导引、控制其飞行弹道,将战斗部导向并摧毁目标的武器。导弹的气动布局直接决定其整体的气动特性[1-2]。文中主要研究十字型尾翼导弹的气动特性,十字型尾翼导弹布局有以下特点:1)各个方向均能产生最大的机动过载;2)升力的大小和作用点与导弹绕纵轴的旋转无关;3)在任何方向产生升力都具有快速响应的特性,大大简化了控制与制导系统的设计;4)在大攻角情况下,将引起大的滚动干扰,这就要求滚动通道控制系统快速性好;5)由于翼面数目多,必然质量大,阻力大,升阻比小,雷达反射面积大[3-5]。

导弹气动特性的分析对于导弹模型结构的优化有着重要的研究意义。气动参数描述空气动力和力矩随着飞行速度、高度和姿态变化的规律,是建立导弹动力学方程的基础。在导弹研制的过程中,飞行控制系统就是根据导弹的气动参数来确定的。研究空气绕流此导弹模型的流动情况,并分析导弹在不同马赫数和不同攻角时的力矩、阻力系数、升力系数和翼型力矩系数变化曲线。

1 理论基础

1.1 基本方程组

模型采用了密度基求解的方法,以速度分量、密度作为基本的变量,压力则由状态方程获得。密度基求解方法是耦合算法,联立求解连续方程、动量方程、能量方程,然后顺序求解其他的标量方程[6]。

如下分别为连续性方程、动量守恒方程、能量守恒方程所组成的方程组:

式中:ρ为流体密度;T为温度;k为流体的传热系数;ST为流体的粘性耗散项;cp是比热容。

1.2 湍流模型

湍流是流体的一种流动状态。这时的流体作不规则运动,有垂直于流管轴线方向的分速度产生,这种运动称为湍流[7]。图1所示为其结构图,图2为能量梯级图。

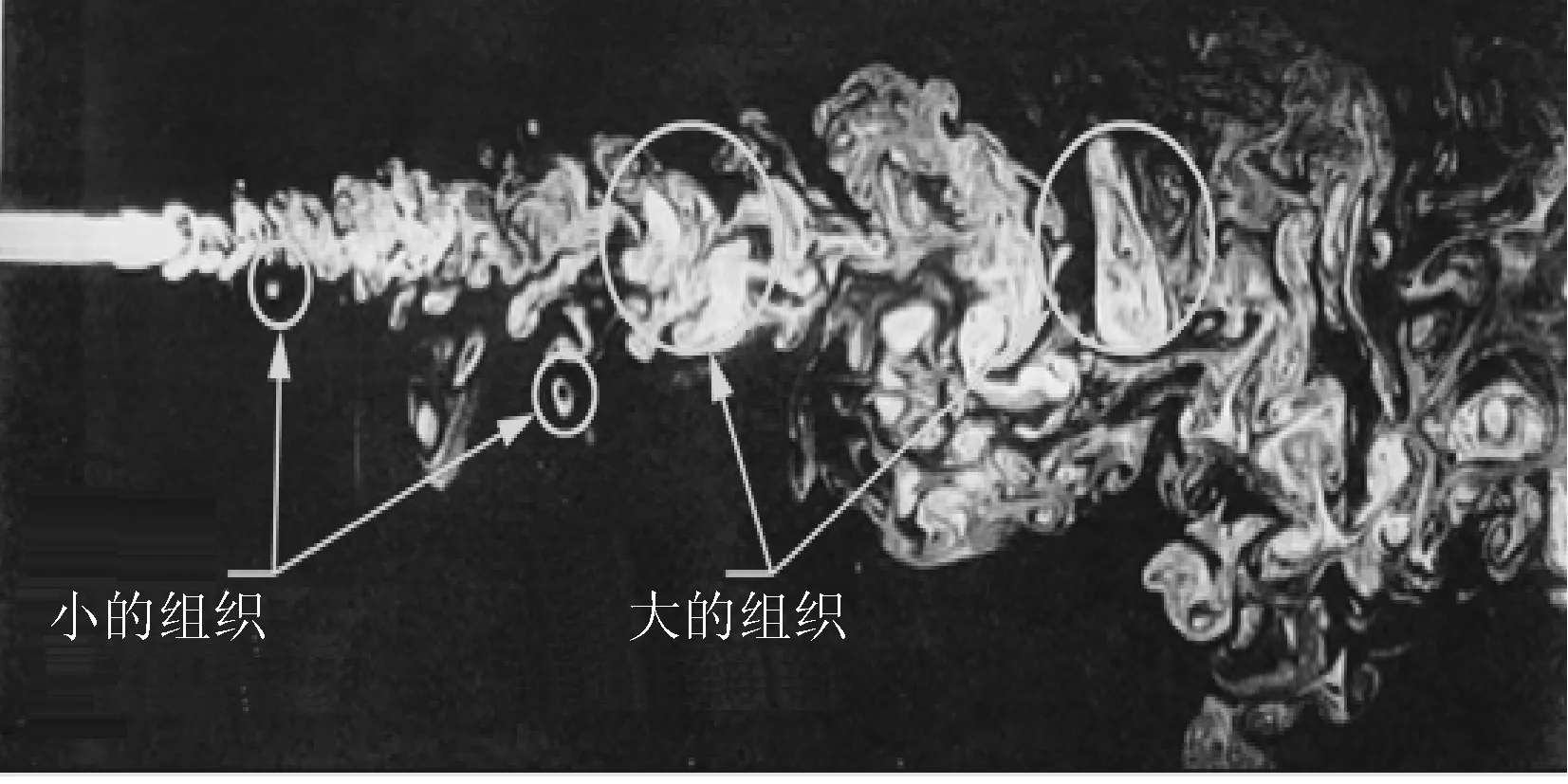
图1 湍流结构结构图

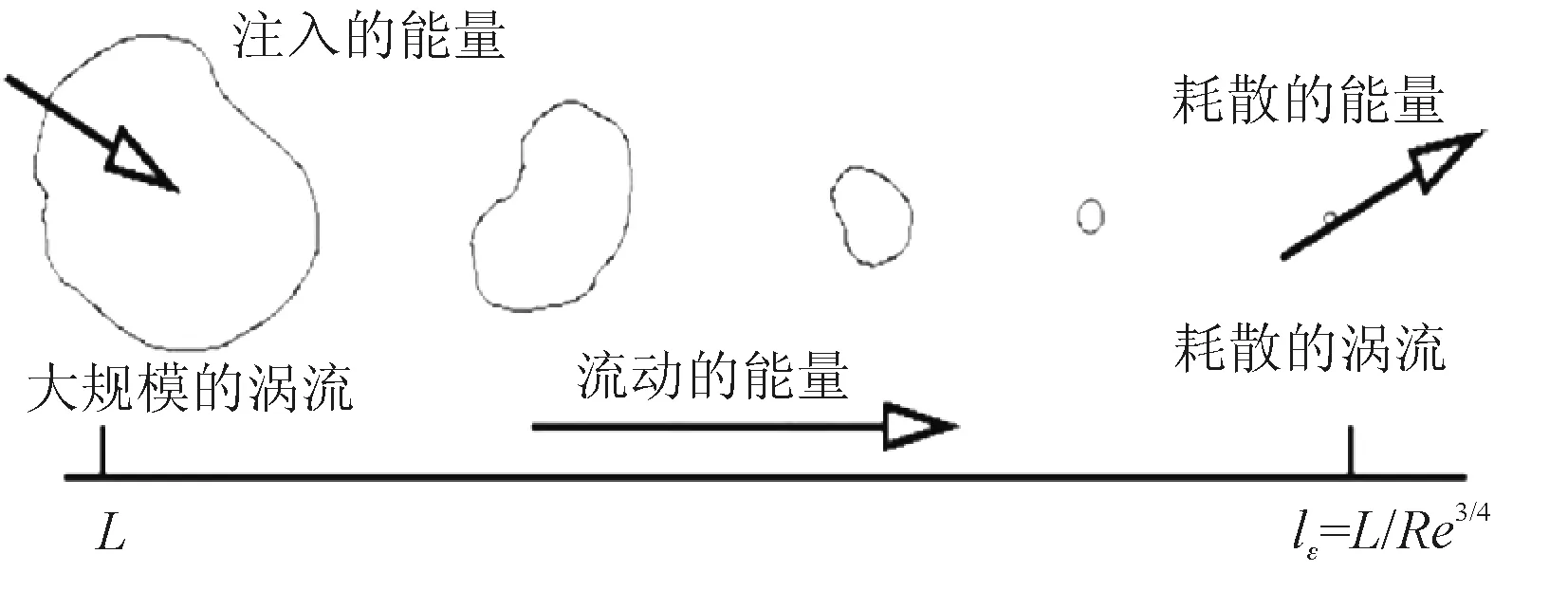
图2 理查德森能量梯级

湍流模型采用Spalart-Allmaras模型。Spalart-Allmaras模型是一个相对简单的单方程模型,解决了针对湍流运动学粘度输运方程模型。该模型是专门为航空航天应用所设计的,涉及wall边界内的流动。Spalart-Allmaras模型相对于两方程模型有计算量小、稳定性好的优点,计算网格在壁面的加密程度与零方程模型有同等的量级[8-9]。

采用Spalart-Allmaras模型输运方程作为控制方程,其形式为:

2 计算模型

2.1 几何建模

利用三维建模和二维建模软件建立导弹的普通化三维实体模型,图3为导弹的二维模型,图4为导弹的三维实体模型。作为研究最普通化的导弹模型,其有导弹弹体和舵翼组成。舵翼在弹尾成对称式分布,主要起改变导弹的飞行姿态的作用。

其中导弹模型的弹直径为D,弹翼的高度和弹直径的关系为D0=2D,导弹前弧度长度为L1=3D,尾翼长度为L2=1.6D,L3=0.75D,导弹模型的总长度为L=11.5D。

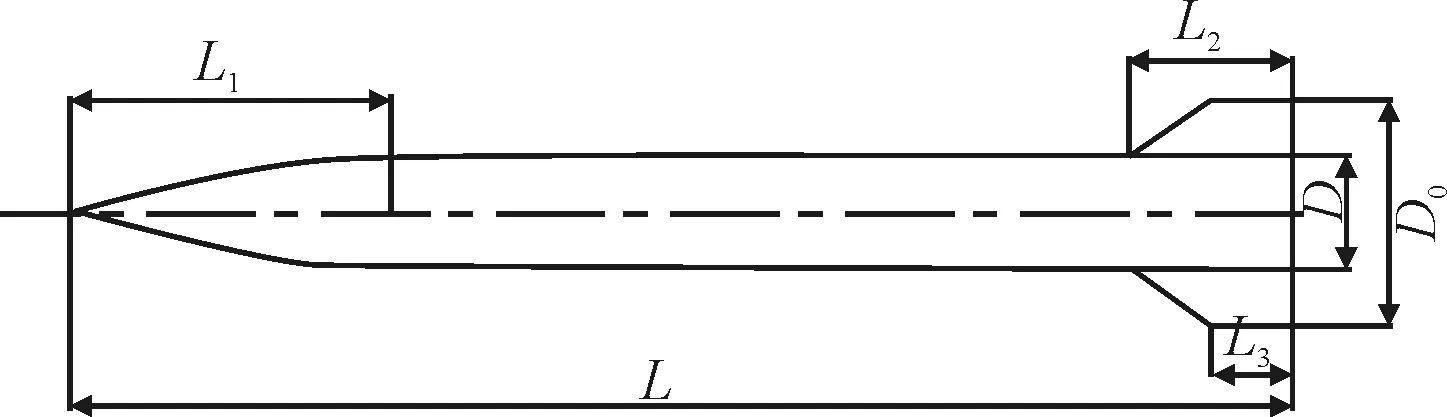
图3 导弹二维模型

图4 导弹三维模型

2.2 数值计算

模型网格划分模型如图5和图6所示,整个流场域分为外层和内层两个计算域,内层计算域采用了网格加密的办法,使得计算更加精确。整个计算域网格数约为200万。将划分好网格的导弹流场域导入Fluent中进行计算。

图5 导弹流场域及网格模型

3 计算结果分析

3.1 动态监控窗口分析

经过计算的过程中设置了动态显示阻力系数、升力系数和力矩系数随着迭代过程变化的曲线,如下图所示,从这些曲线可以看出阻力系数、升力系数和力矩系数的变化规律,在迭代3 000次的时候,阻力系数(Cd)、升力系数(Cl)和力矩系数(Cm)变化不大。说明此时所受的阻力、升力和翻转力矩基本不再变化。

残差曲线表示的是各个方程迭代的收敛情况,如图7所示的残差曲线图可以看到通过计算在3 000次迭代步数时残差值的变化范围在1e-3～1e-4范围之内,在所要求的1e-3之内,而且幅度变化很小,因此可以说此时计算达到收敛状态,可以进行后续的数据。

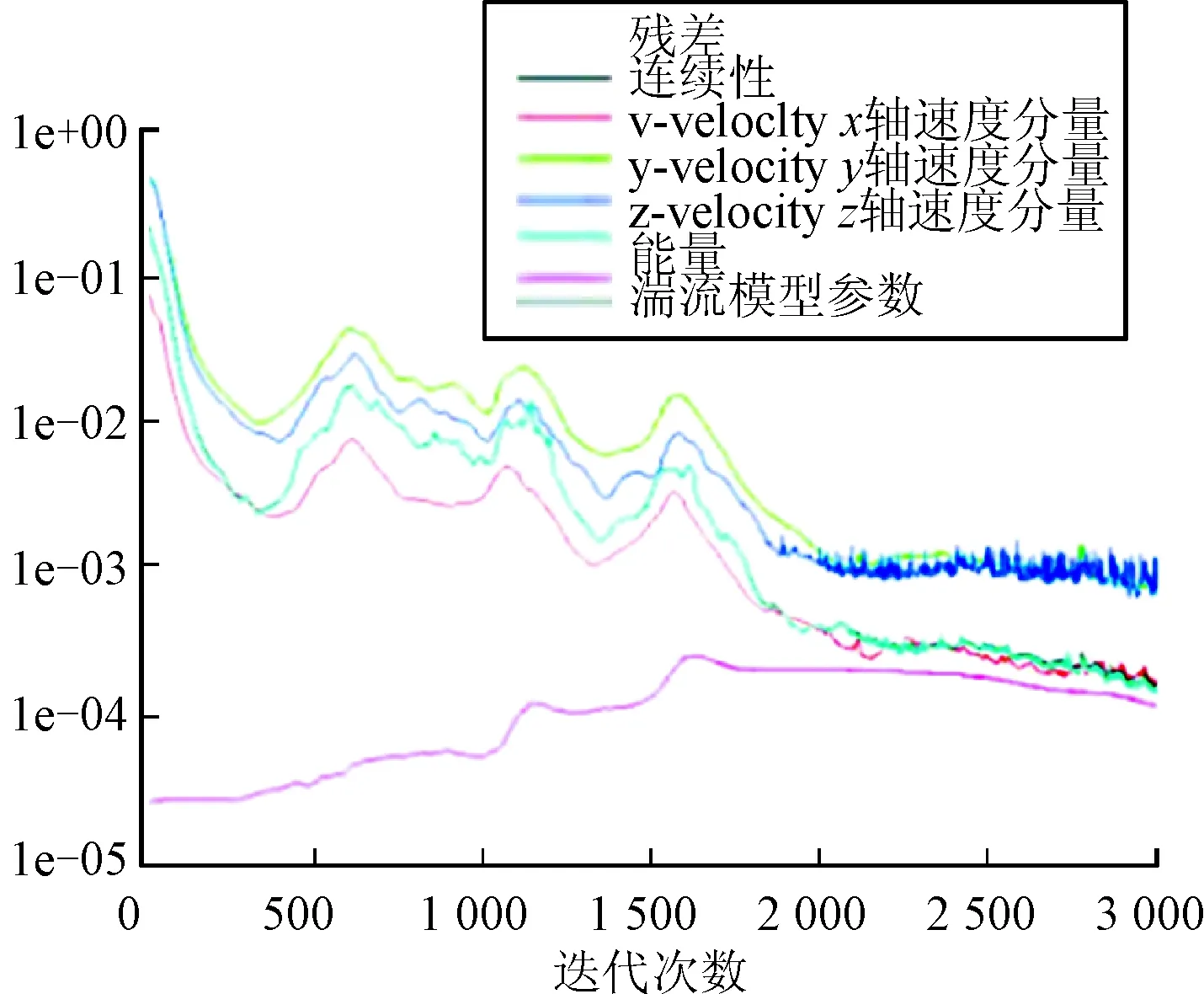
图7 残差曲线图

图8、图9和图10的阻力系数、升力系数和翼型力矩系数的变化曲线图也可以验证残差曲线图的变化趋势是否达到收敛。通过图8、图9和图10我们可以发现阻力系数、升力系数和翼型力矩系数在迭代过程中前1 500次迭代步数之前阻力系数、升力系数和翼型力矩系数还有较大的变化,而在迭代到2 000步的时候,各系数基本变化幅度很小,曲线基本保持平稳状态,达到使用要求,此时可以得到阻力系数。

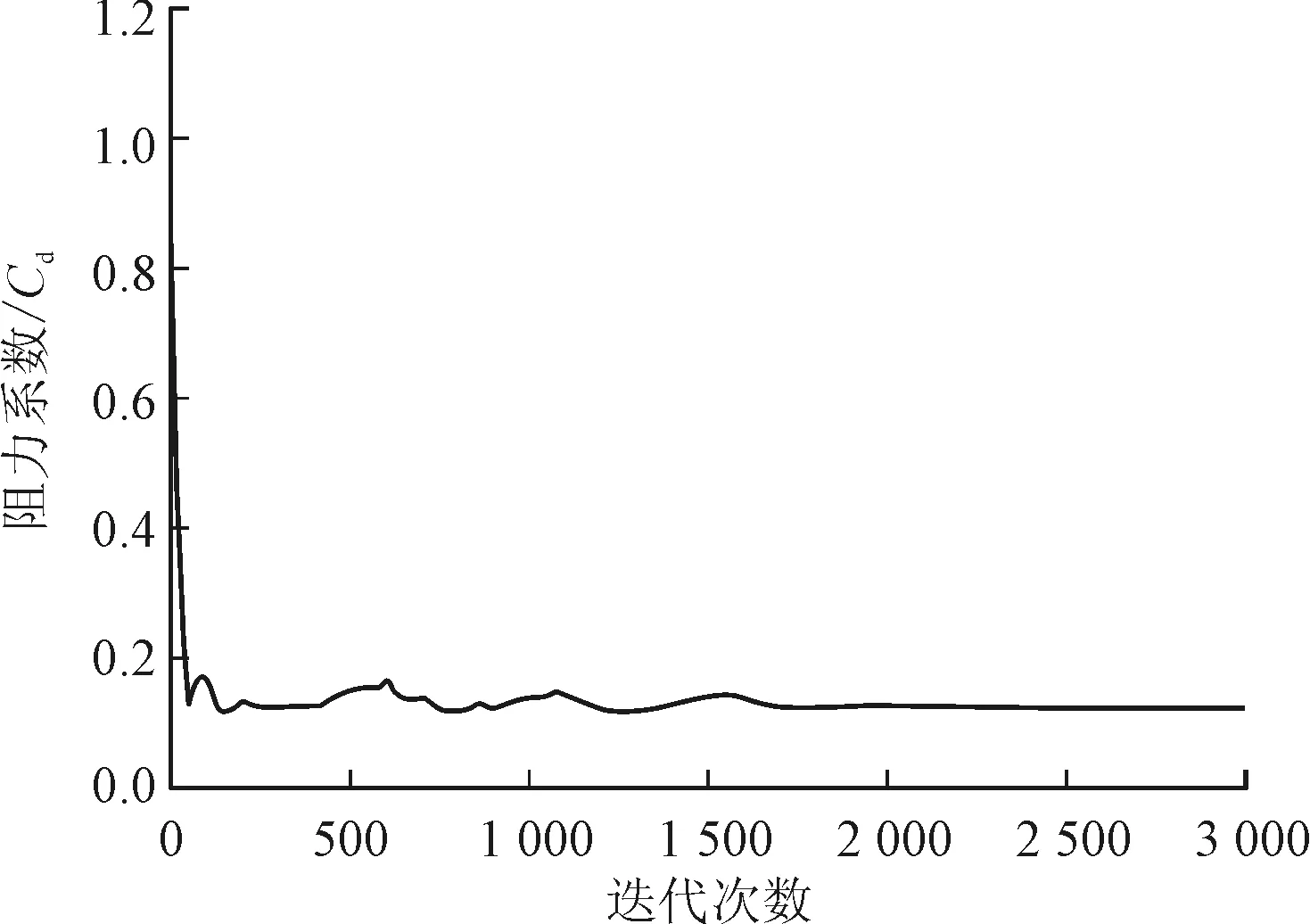
图8 阻力系数随迭代过程变化曲线

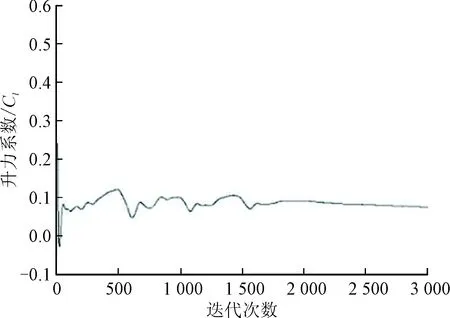
图9 升力系数随迭代过程变化曲线

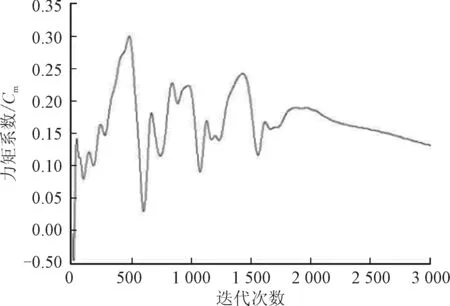
图10 翼型的力矩系数随迭代过程变化曲线

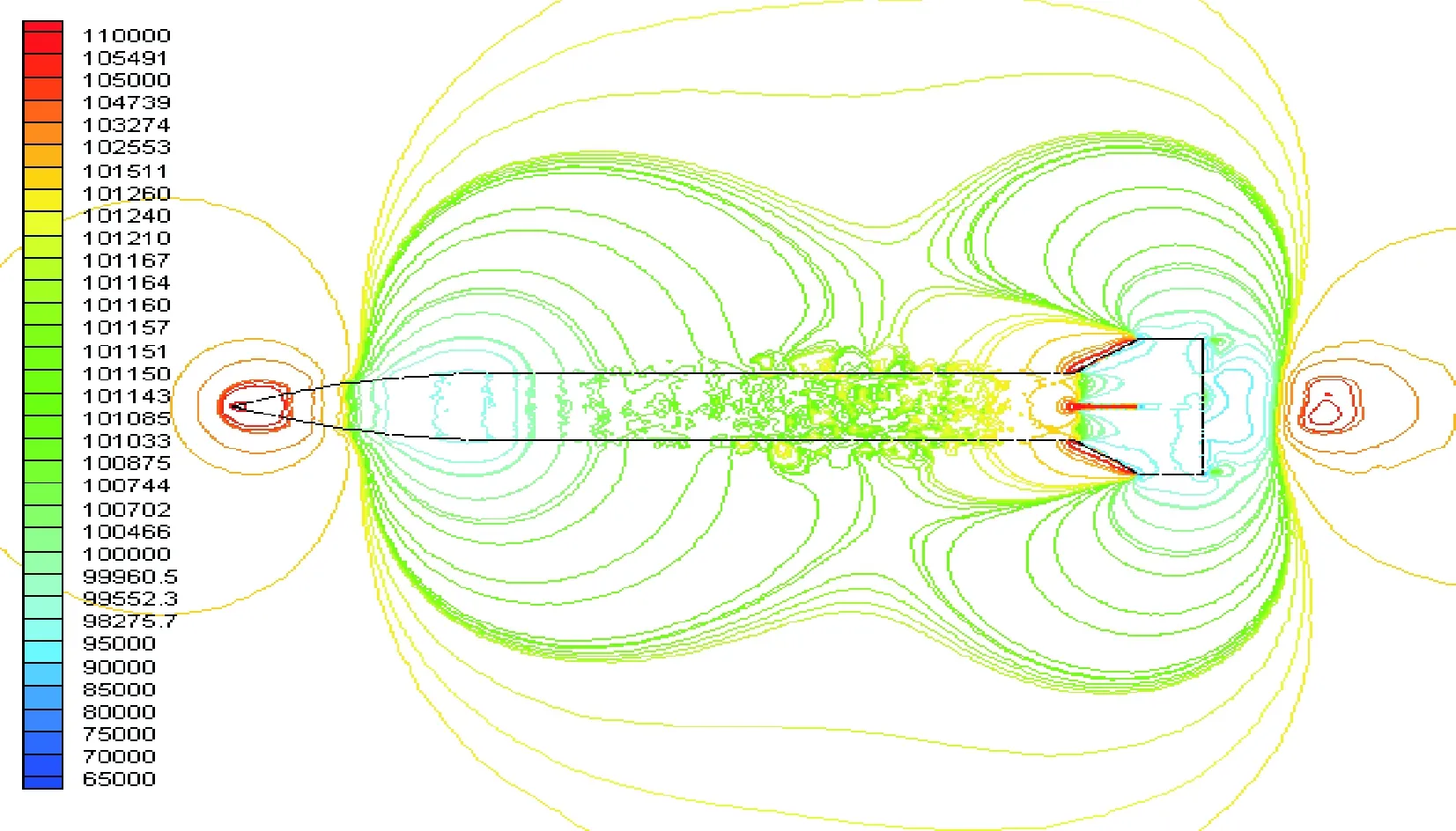
图11 0.6 Ma时压力云图

3.2 空气绕导弹流动情况

图11、图12、图13、图14和图15是攻角为2°时,十字型尾翼弹的压力云图。图11和图12为导弹亚音速飞行时导弹周围流场的压力云图可以看出当亚音速飞行时,导弹周围的空气流场只受到摩擦和涡阻的作用。图13为跨音速飞行时,即当飞行速度为1Ma时导弹不仅仅受摩擦和窝阻作用,而且还受到局部激波作用,所谓的激波飞行器高速飞行,超声速的气流突然压缩等流动中,往往会出现流动参数发生显著、突跃变化的现象。实际上,激波是很薄的一层,它的厚度是分子自由程的量级。在这一薄层中,物理量(温度、速度、压强)迅速的从波前值变化到波后值,速度梯度、压强梯度和温度梯度都很大。图14和图15为导弹超音速飞行,当超音速飞行时,弹体受到的空气阻力主要是波阻,从图中可以看到其产生了头激波和尾激波[5]。

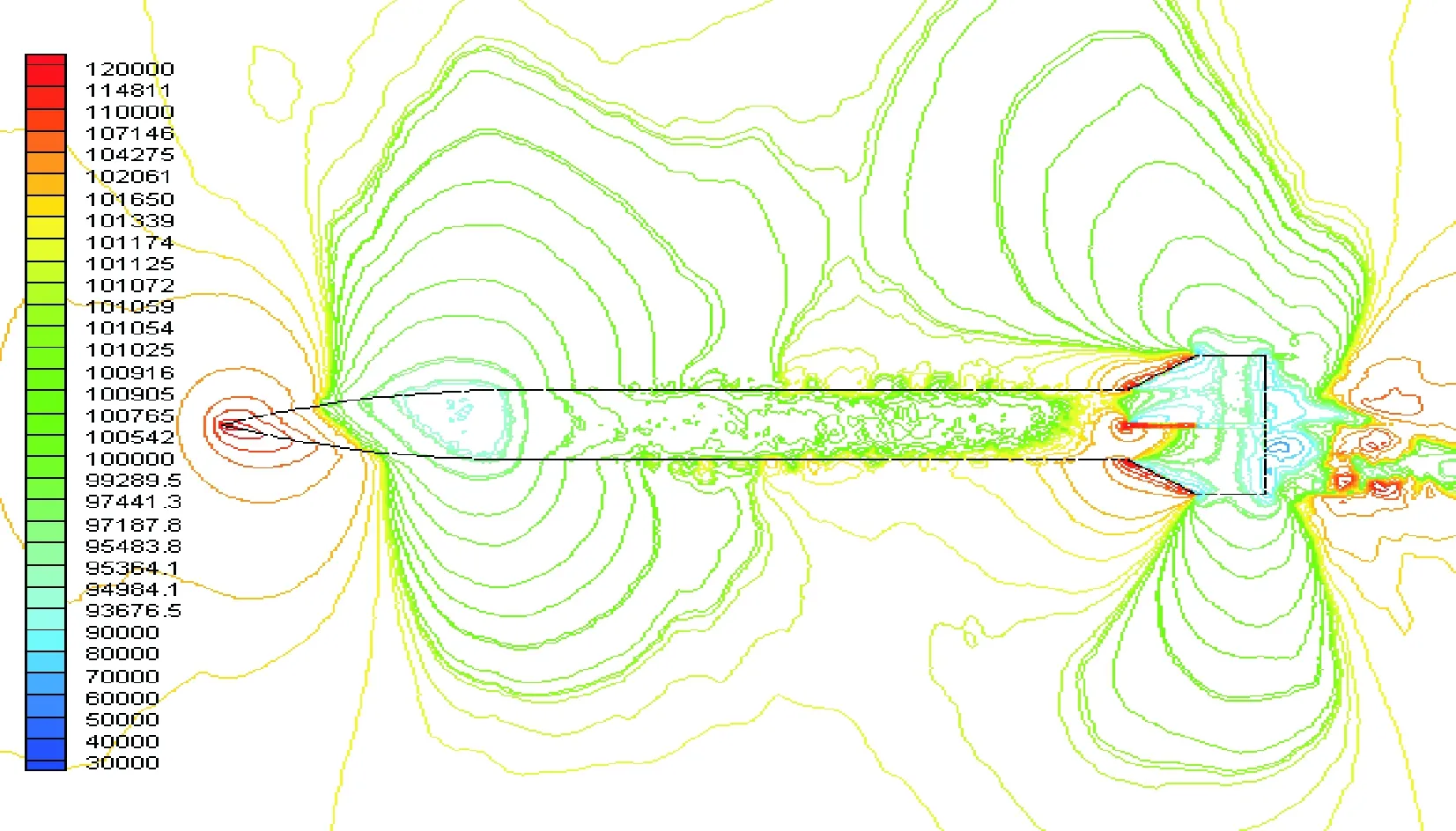
图12 0.8 Ma时压力云图

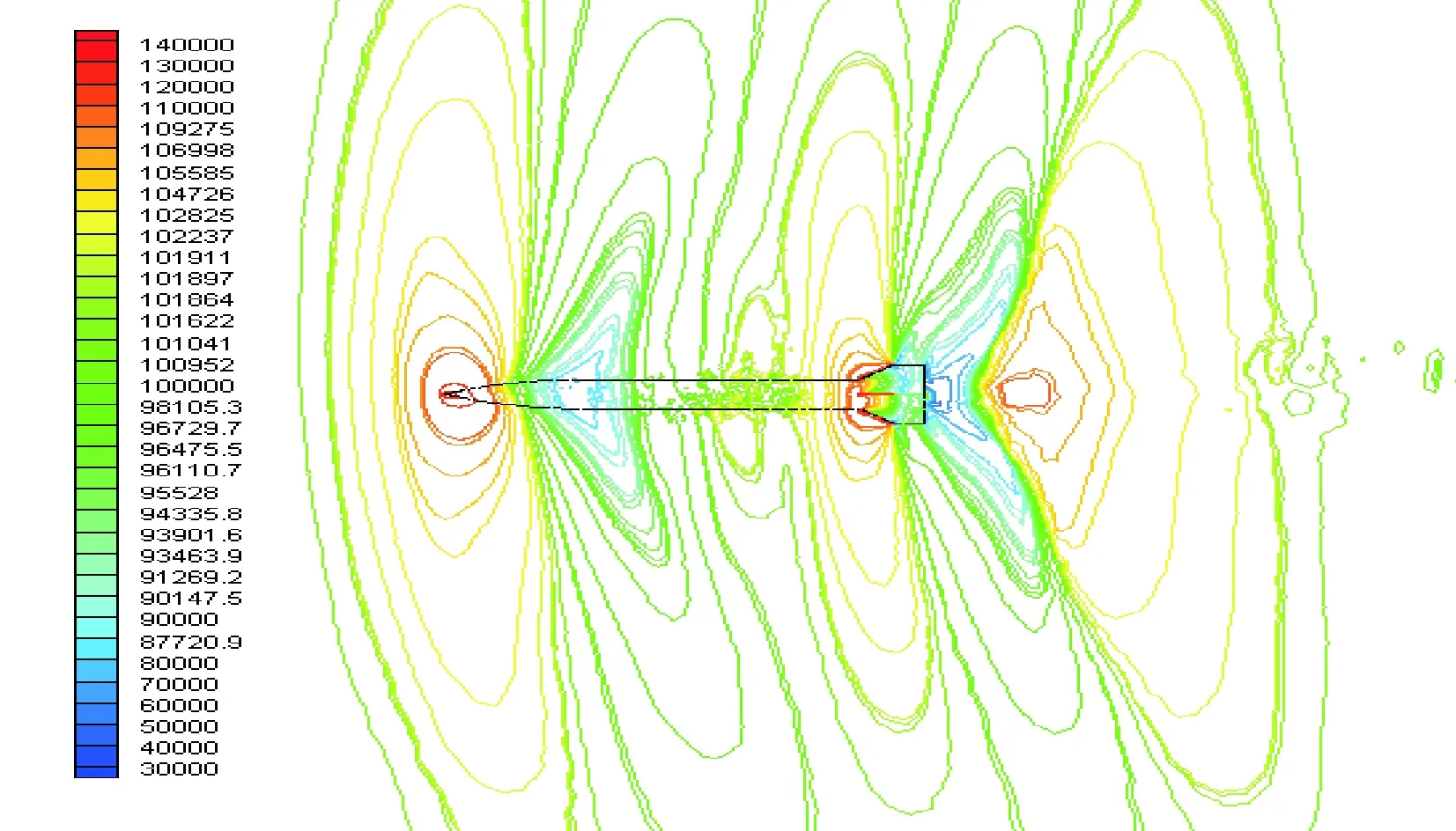
图13 1 Ma时压力云图

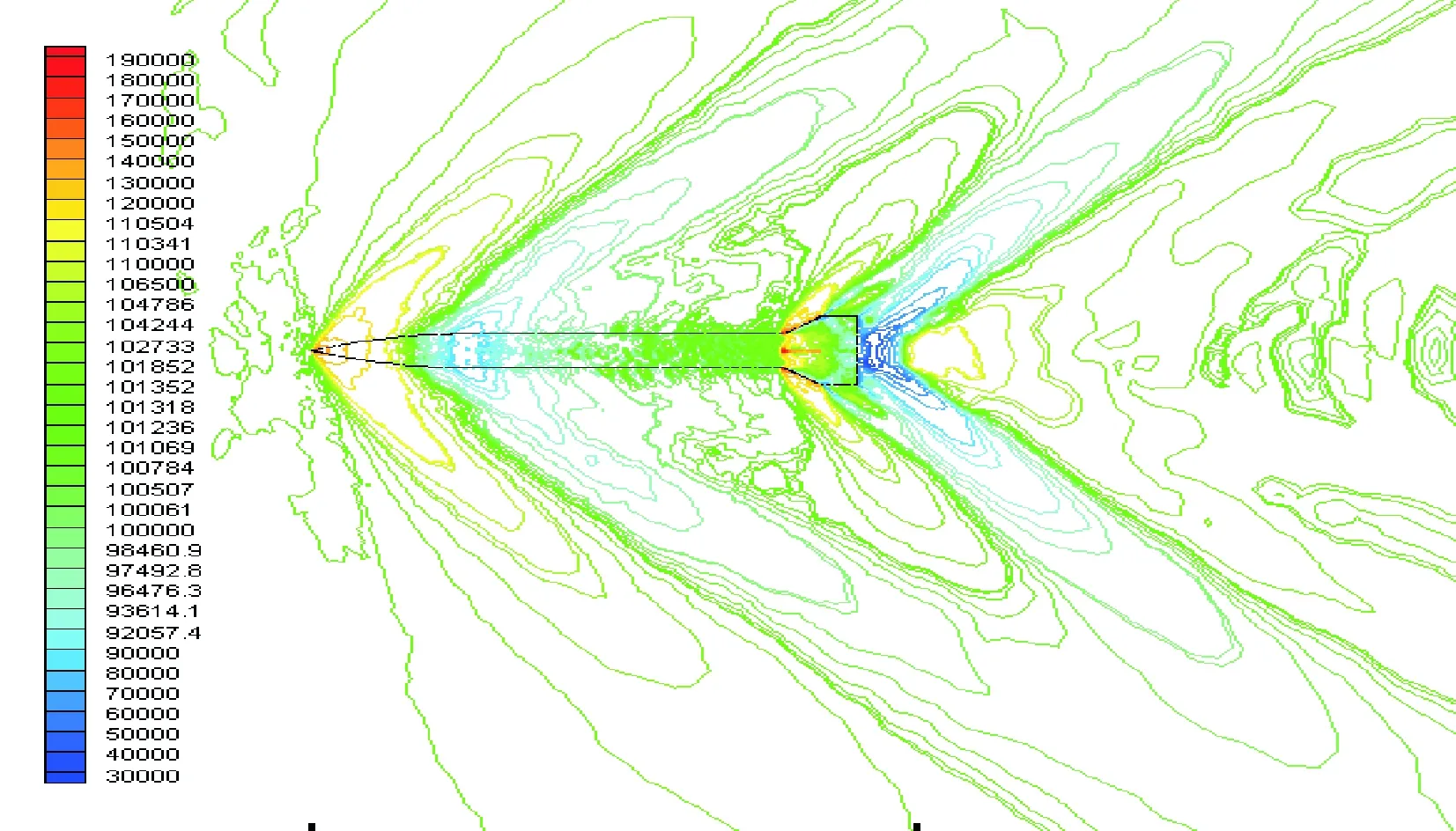
图14 1.2 Ma时压力云图

图15 1.4 Ma时压力云图

从以上各图可以得到,亚音速、跨音速和超音速这三个不同的飞行速度,导弹模型所受到的不同的力会发生巨大变化,因此为今后导弹设计提供了必要的帮助,对于如何减少阻力、摩擦和涡阻提出了要求。

3.3 导弹模型的受力分析

对导弹所受的阻力和阻力系数、升力和升力系数、翻转力矩和力矩系数进行分析,通过对cd-history、cl-history和cm-history读取可以得到最终收敛的阻力、升力和力矩值。

从图16中可以发现阻力随着马赫数的增大而增大,当飞行速度由0.6Ma升至0.8Ma时阻力增幅最大,而阻力基本不随攻角的变化而改变。从图17可以看出在攻角为0°时,升力基本为0,在攻角大于0°时,升力随着马赫数增大而增大,而在超音速升力上升趋势比亚音速更大。从图18可以看出翻转力矩的变化趋势,当攻角为0°时,翻转力矩几乎为0,攻角一定的情况下,翻转力矩随着马赫数的增大逐渐增大,大于1Ma时的增加率高于1Ma时的变化率。

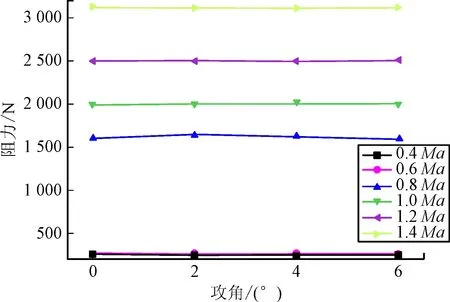
图16 阻力随马赫数和攻角的变化曲线

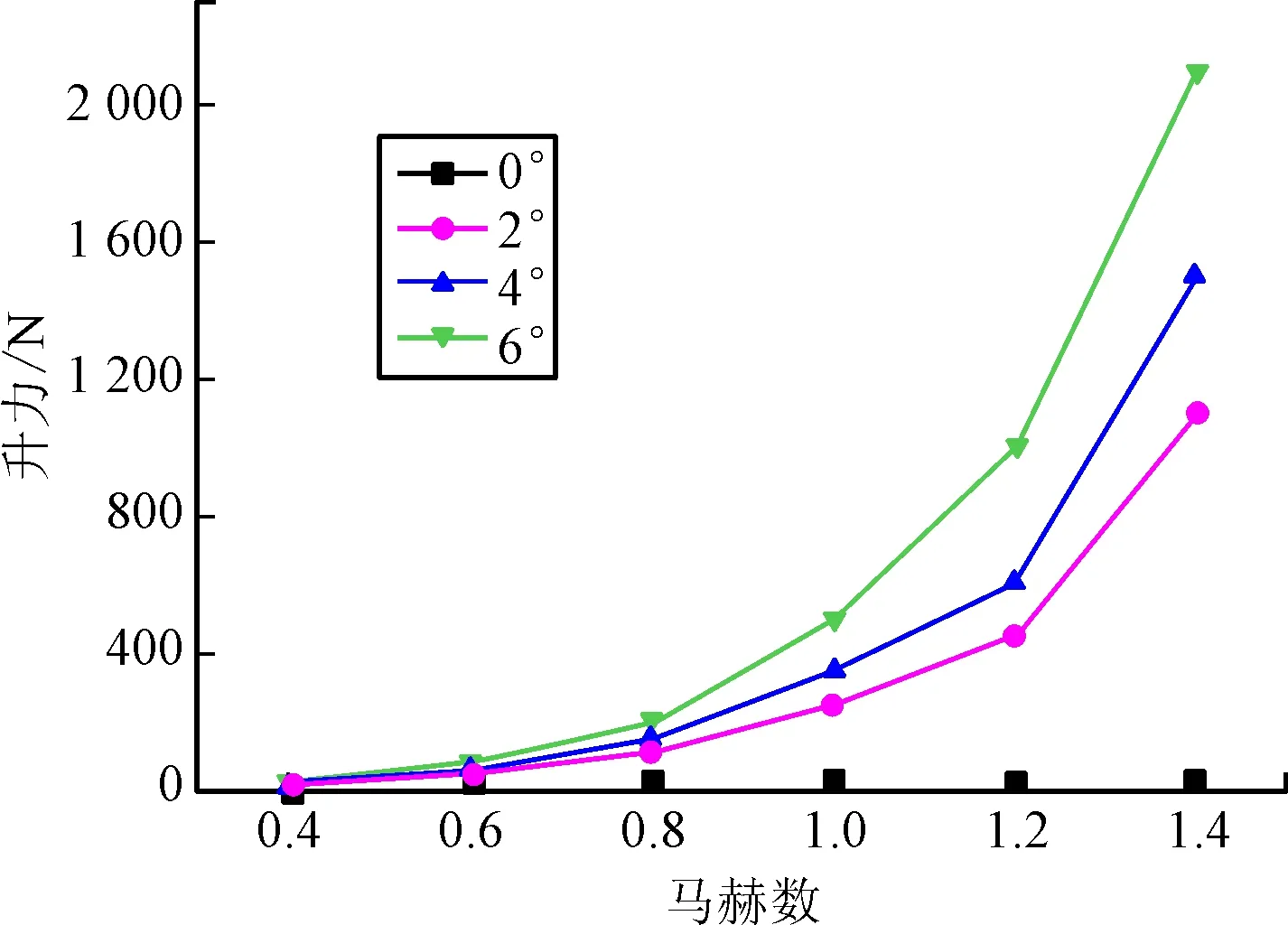
图17 升力随马赫数和攻角的变化曲线

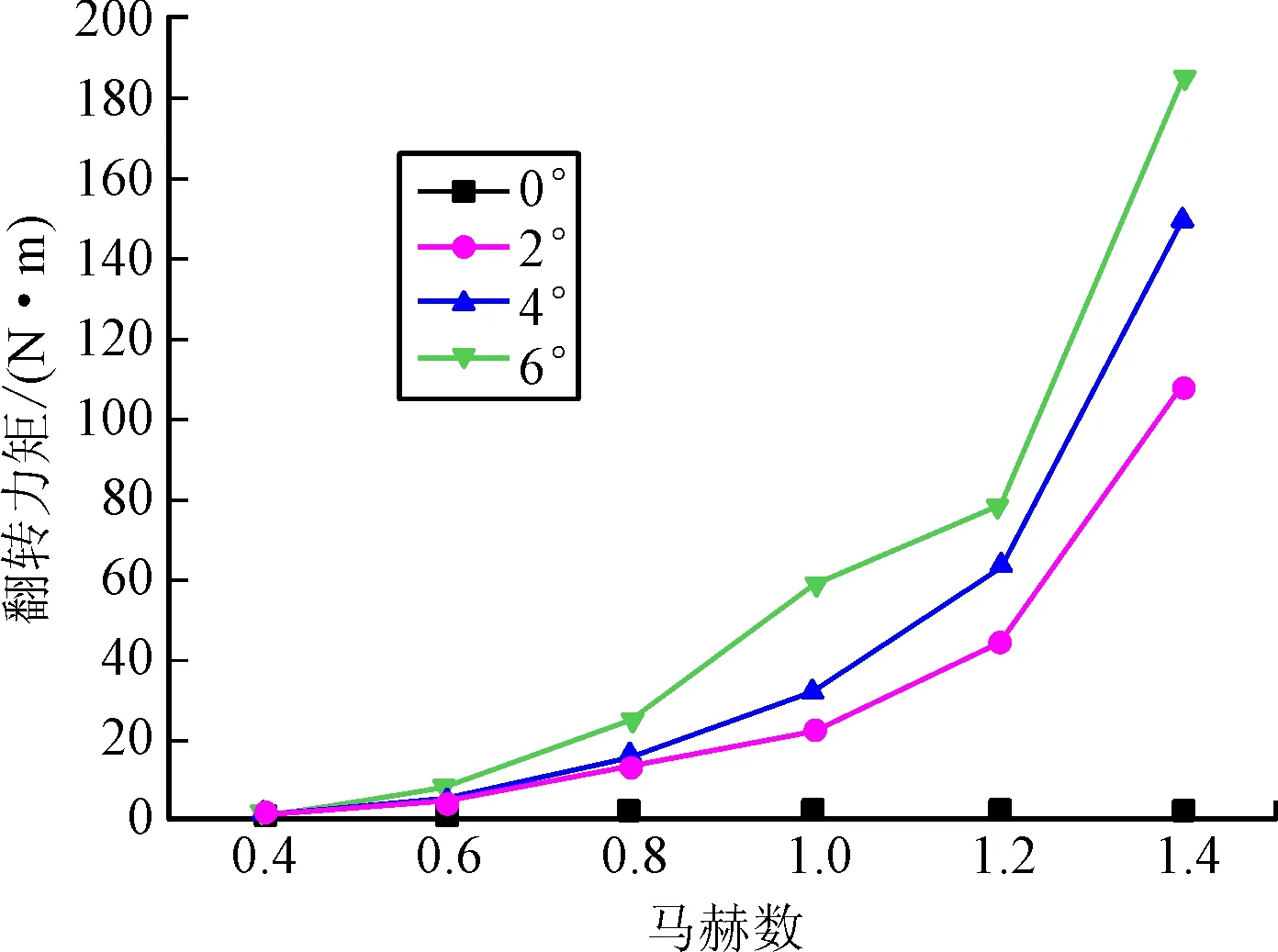
图18 翻转力矩随马赫数和攻角的变化曲线

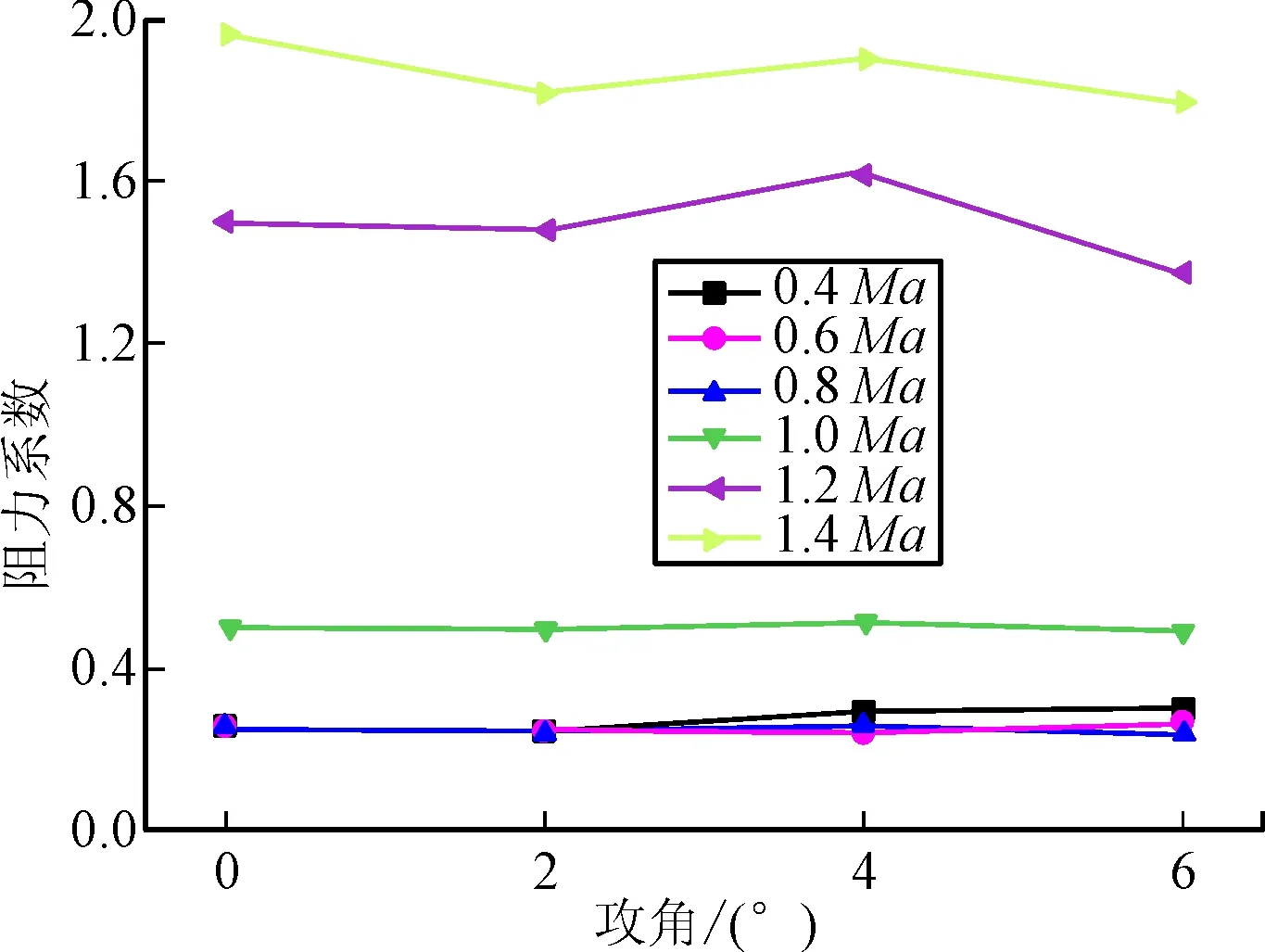
图19 阻力系数随马赫数和攻角的变化曲线

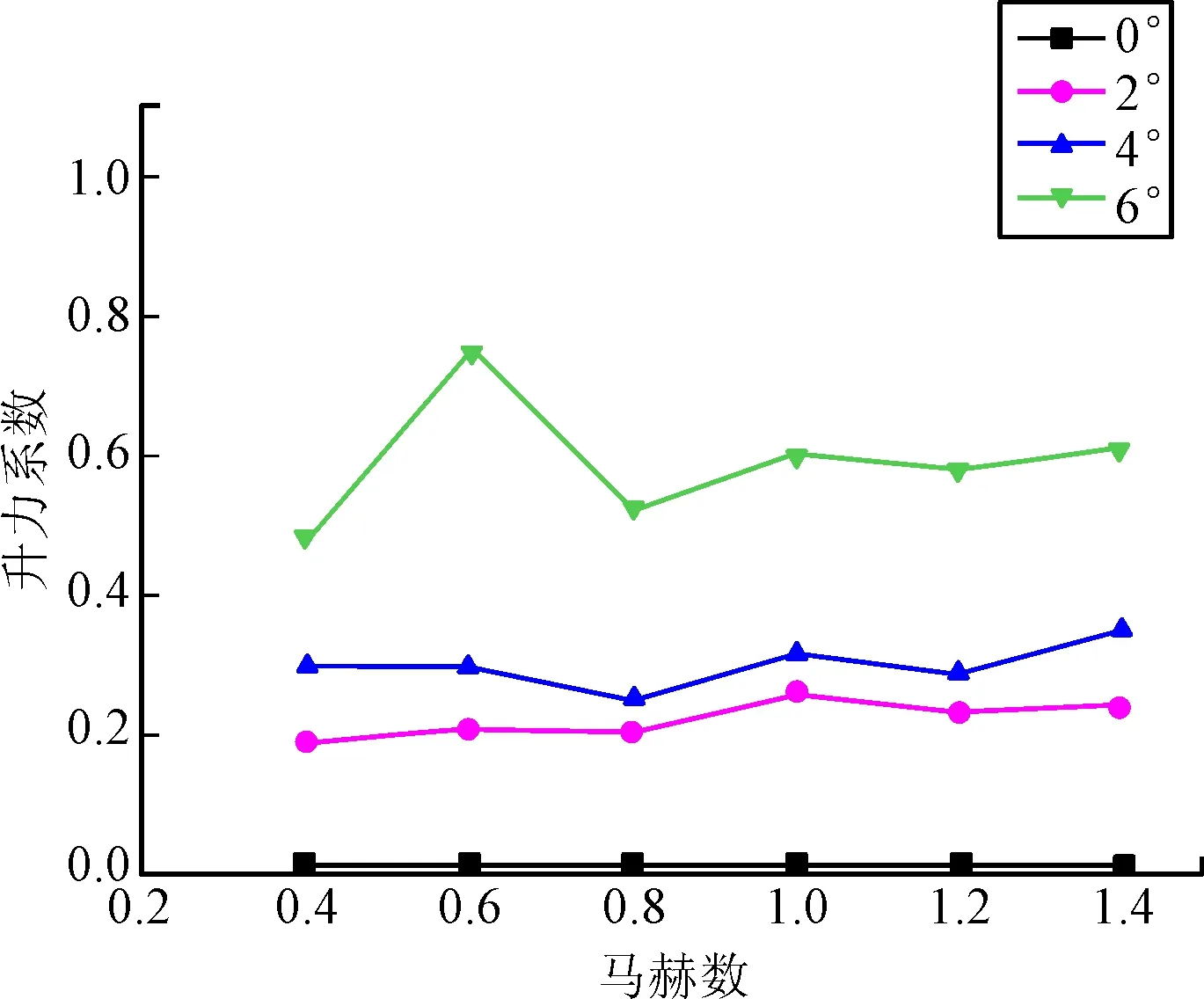
图20 升力系数随着马赫数和攻角的变化曲线

图19和图20所示为十字型尾翼导弹在不同攻角和不同马赫数下的阻力系数、升力系数变化的规律。从图19可以看出,阻力系数的变化在亚音速基本保持不变,随着飞行速度不断增大,大于1Ma时阻力系数不断增大,从1Ma到1.2Ma增大最多。图20为升力系数的变化规律,随着攻角的增大,升力系数逐步增大,飞行速度对升力系数影响不大。

阻力特性在研究导弹的设计过程中有着重要的作用,只有知道阻力特性,才能去不断改进导弹的气动布局,从而想办法去减少其在飞行过程中所受到的阻力。导弹所受到的升力直接影响导弹的飞行品质,对导弹能否精确的命中目标有着影响。导弹在飞行过程中如果有攻角,就会产生影响导弹飞行稳定性的翻转力矩,如果在飞行过程中受到较大的力矩的作用,导弹会发生翻转的趋势,可能会影响导弹设计的精度,因此分析翻转力矩变化规律,可以减小翻转力矩,实现导弹飞行的稳定性。

4 结论

结果表明:

1)十字型尾翼弹在亚音速、跨音速和超音速飞行时空气绕导弹的流场情况有很大不同,在亚音速受到的阻力为摩擦阻力和涡旋阻力。在超音速时,受到的阻力主要为波阻,会出现强烈的激波现象。

2)在飞行过程中导弹受到的阻力随着马赫数的增大而增大,而随攻角的变化不大。升力和翻转力矩随着马赫数的增大而增大,攻角越大升力越大。

通过文中的分析可以看出如何减小阻力和翻转力矩,提高升力是研究的下一个方向,通过改善导弹的气动特性,从而实现导弹飞行的稳定和提高导弹的命中率,对未来的作战有着重要的意义。