浅谈正项有界周期数列的一些性质

◎王礼斌

一、有关数列简介以及例题详解

1.等差数列的函数思想。

2.数列角标联系。

3.双数列的联系。

4.数列的单调性。

（1）以正数开头的递减扥差数列的前n项和的最大值是所有非负项之和；反之，以负数作为开头的递减等差数列前n项和的最小值是所有非正项之和。

（2）对于等比数列｛an｝，若 a1＞0，q＞1，则｛an｝为递增数列；若 a1＜0，q＞1，则｛an｝为递减数列；若 a1＞0，0＜q＜1，则｛an｝为递减数列；若a1＜0，0＜q＜1，则｛an｝为递增数列；若q＜0，则｛an｝为摆动数列；若 q＝1，则｛an｝为常数列。

例题1

已知数列｛an｝，｛bn｝，｛cn｝的通项公式满足 bn＝an＋1－an，cn＝bn＋1－bn（n∈N*）

若数列｛an｝，首项 a1＝2，且满足 cn－bn＋1＋3an＝2n＋1（n∈ N*），求数列｛an｝的通项公式。

分析：cn－bn＋1＋3an＝2n＋1（n∈N*），可得 bn＋1－b－bn＋1＋3an＝－2n＋1，即 bn－3an＝2n＋1，所以 an＋1＝4an＋2n＋1，在等式 an＋1＝4an＋2n＋1，两边同时除以 2n＋1

所以kn＋1＝2·2n－1＝2n，即kn＝2n－1.所以an＝2n·kn＝2n（2n－1）＝4n－2n

构造数列｛kn｝是此题突破之处，对不熟悉的递归式的变形通常是为了构造新的数列，让不熟悉的递归式转化为熟悉的递归式。

例题2

已知数列｛bn｝的通项公式为bn＝n.在bk和bk＋1（k∈N*）之间插入3k＋1个3得到一个新的数列｛dn｝，问是否存在这样的正整数m，使得数列｛dn｝的前m项的和Sm＝2008，如果存在求出m的值，如果不存在请说明理由。

插入项后组成新的数列，对新数列项的构成要做具体分析，具体做法仍然是用基本量解决问题。本体在具体计算的过程中用到估算思想，希望同学们引起关注。

例题3

n2（n≥4）个正数排成n行n列

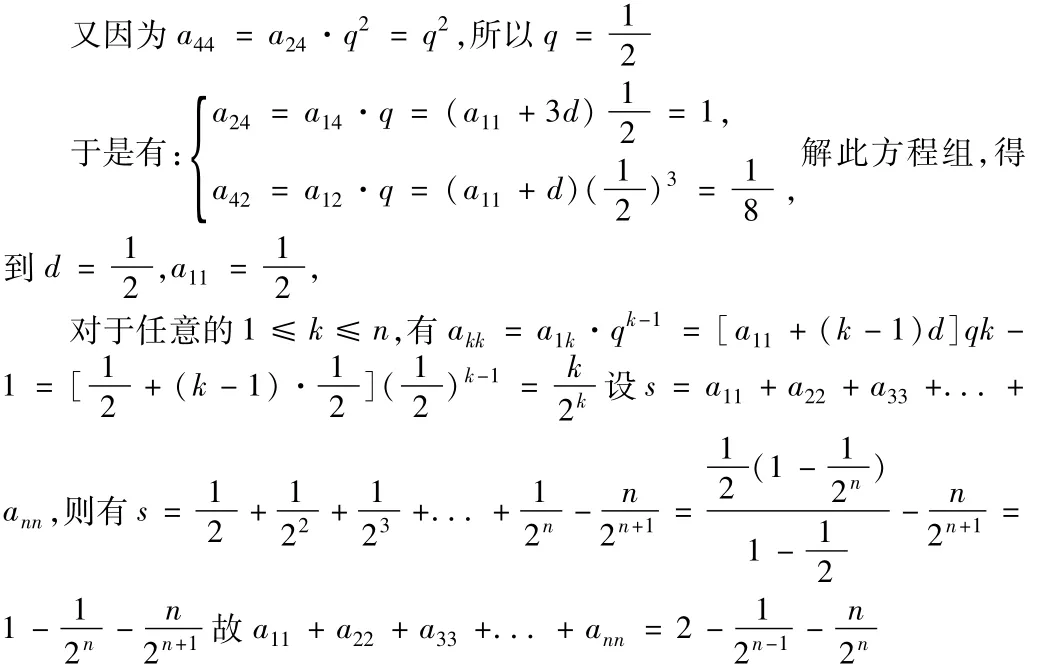
高考数学通常把考查数列的试题作为压轴题，而且许多难度大的数列试题往往是由高中竞赛数学的试题改编而来的。这道题的关键的尽可能多地将文字信息转化为数学的关系式。

二、近年高考例题解析

2015年的一道数列高考题十分有特点，下面列举和大家一起分析一下。题目如下：

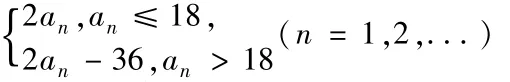
（1）若a1＝6，求集合M中所有元素

（2）若集合M中存在以个元素是3的倍数，证明：M的所有元素都是3的倍数.

（3）求集合M的元素最大值.

此题着重考查了递推数列，立意新颖。第三个问题还考查了学生对数学的敏感性，同时也给其他考生留了一条出路——枚举法。这一问题，既有难度，又无难度，是一道难得的好题。解答问题3

记Card（M）为集合M的元素个数，由于a2一定是偶数，故a3一定是4的倍数，因此，可以从a3开始讨论，容易知道数列｛an｝中任意一项都是不大于36的正整数，并且an（n≥3）均为4的倍数，故an（n≥3）可取4（k＝1，2，...，9）.若a3是3的倍数，则由（2）可知，an（n≥3）只能取12，24，36，故此时 Card（M）≤5；若 a3不是3的倍数，则 an（n≥3）只能取4，8，16，20，28，32，故此时 Card（M）≤ 8；又 a1＝1时，M ＝故Card（M）最大值为8.

由此的拓展

当 a1＝6k±1时，Card（M）都可以取到最大值.当a1＝9，18，27，36时，数列有极限，当a1为其他值时，存在N0∈N*，当n＞N0时，数列为周期数列，因此出现以下问题：

若P为素数，a1·s∈N*，a1≤ps，

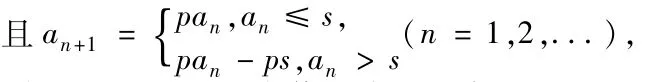
则（1）Card（M）最大值是多少？当Card（M）取到最大值时，首项是多少？

（2）若数列有极限，则首项是多少？

（3）该数列是否要么有极限，要么存在N，当n＞N时，数列是不是长数列的周期数列

（4）若首项取任意值，数列都有极限，那么p，s要符合什么条件？

对于（3），当p≠2且a1＝ps时，则集合M一定是无限集；所以考虑另一种推广：an＋1＝p［an－（k－1）s］，（k－1）s＜an≤ks，其中1≤k≤p.由于分段较多，可以对PS取模，此时（3）显然成立。其他有关问题得到结果如下：

定理的证明（1）记f（s，a1）是由s和a1确定的，集合M的元素个数，f（s）＝max f（s，a1），即 f（s）是 Card（M）的最大值，令 （i，a1）＝q成立.

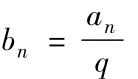
由 ps｜（an＋1－pan），q｜ps，t｜s，

知 q｜（an＋1－pan），t｜（an＋1－pan），

由归纳法知∀n∈N*，有q｜an及（t，an）成立.

由｛bn｝的构造可知 p｜b2，故由归纳得 pa＋1｜ba＋2；

即对 ∀n≥ a＋2，pa＋1｜b成立.

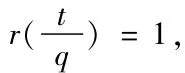
故当n≥a＋2时，bn＝pa＋1

再由r*的最小性可知：

c1，c2，......cr*互不相同，

因 r*≤ r（t），

＝a＋1＋r*≤a＋1＋r（t）；

综上可知：

f（s）＝a＋1＋r（t），当 β＝a＋1，r*＝r（t）时，等式成立.

即当（p，a1）＝1，r*＝r（t）时，Card（M）最大值 a＋1＋r（t）