新课改下高中数学课堂教学新模式浅谈
◎胡旋
一、重视体验,突出过程
数学是思维的体操,数学学科教学在培养学生的理性思维方面发挥着独特的不可替代的优势。数学教学注重培养学生的理性思维,就是将数学教学和学生的数学学习变得自然和理性,回归数学的教学本质。这种自然和理性不仅贯穿于数学知识的发生发展过程,融于数学思想方法的发掘与整理过程,同时也影响数学课堂的活力,有助于学生的学习志趣的形成,促进数学思维的发展,也有利于教师的专业发展。
理性思维的训练建立在学生的积极主动的数学思考上,然而,不少教师独霸课堂,课堂成为一言堂,整节课按照自己的预设不折不扣、按部就班。教师独领风骚,学生亦步亦趋。一节课下来,教学任务如期完成,自己倍感成就。面对自己的大难度高水平技巧,学生满眼崇拜,教师心怀自豪。也有时学生缺少回应,教师便生疲惫之感,嗓子冒烟,心急火燎,尤其发现学生听着带劲,解题不会,期待下节,再来相会。于是,很有可能陷入泥潭不能自拔,长期如此,教师上课忙碌,学生上课休息,课堂上根本没有学生的内在体验,学生很少学会思考,学会了等待教师的展示。知识---教师----学生,如果对三者在课堂上的呈现关系缺乏正确的认识,就会忽视学生的存在,课堂上只剩下知识和教师,学生反而成为课堂之外的元素。课堂上教师角色定位不准确,学生主体性的地位得不到体现甚至被忽视。事实上,知识的获取和理解离不开学习者的主动参与和体验,教师只有让学生增强体验、发展感悟,学生才会在课堂上主动参与,达到积极学习的状态。
二、构建良好教学情境
在数学教学过程中,情境一般以问题情境出现的形式居多,数学是由问题构成的,数学教学过程实质上是数学问题解决的认知过程。教师可以通过一些简单易懂的题的引入学生进入教师已设定的情景中,使学生产生求知欲,继续探索,以打开学生的思维,使学生思维得以发散,也有利于老师对学生学习状态的了解和课堂教学的把控。下面以教师讲授新课“方程的根与函数的零点”为例,这部分内容教师可以创设如下的问题情境:
例:判断下列方程是否有根?
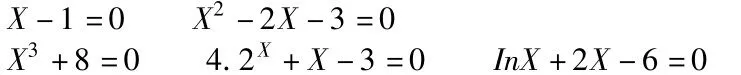
前面三个方程可以根据以往所学的知识对它们进行求解,后面两个方程学生会发现以前学习的知识并不能解决这两个问题,或者更具体的说判断不出根的情况及根的个数,通过问题情境,形成学生的认知冲突,以前学习的知识并不能解决现有的问题,因此学生对于这种若隐若现的方程(形式上感觉是熟悉的)感觉就差一步便能解决,由此激发学生的求知欲,让学生自己发现问题,并主动探索,以至解决问题。
三、重视探究活动的有效落实
探究活动就是让学生自己参与到知识的发生、发展的过程,不仅可以巩固旧知,还可以加深对新知的理解。在社会建构主义理论的基础上,采用讨论探究教学模式,引导学生主动去完成对知识建构,形成自我对知识的表征。再以上面的课例为例:对于方程来讲我们可以得出相对应的函数,函数必然会有函数图像,那方程的根与函数图像有什么关系呢?我们先以一元二次方程研究对象,由此探究出函数零点的定义,并继续启发学生联想到方程的根与函数的零点的关系,继续进行探究活动,让学生自己观察后两个方程的特点,并结合新知寻求可行的办法。最后非常规的方程求根就能够转换成求函数的零点,还能转换成求两个函数图像交点的横坐标。
四、重视对于知识的总结
简单回顾所教的知识,有利于增强学生对课堂知识理解与记忆;简要总结思维方式,有利于推动思维方式在学习上的运用,并促使学生对所学课程有更深的理解。比如说在“方程的根与函数的零点”教学设计的归纳总结为例:教师在进行总结的过程中,就可以结合相关的提问,引导学生进行有效的总结。例如,经过本节课的学习,你有哪些收获呢?我们学习了函数零点的定义其等价关系(有两方面意义:几何意义和代数意义),对于普通的函数我们可以用代数法来判断方程的根和函数的零点是否存在,我们还学会了利用构造函数,画出函数图像,对函数图像进行观察来判断方程的根和函数的零点是否存在,我们把这种方法叫做几何法,更具体的也可以说成构造函数图像法。无形当中向学生展示了,函数的思想方法和数形结合的思想方法来判断方程根的便捷性,更能激发学生对数学思想方法的重视。
五、以作业来激发学生的求知欲
根据新课改的要求,教学应该是面向全体学生,使每位学生都能受到良好的教育,在教学过程中提倡教师分层次的教学。同样的在布置作业这个环节也提倡教师分层次的布置作业,主要由必做题和选做题构成。必做题一般是用来考察学生基础知识学得如何,是否掌握了新知识。选做题一般是布置给有需要的学生完成,让他们在具备基础知识的基础上还能有更大地进步。总之,教师在布置作业进行分层次的布置合理的作业,便可以在课后巩固大部分学生对知识的掌握,有策略的激发学生求知欲和不同层次学生的需求得到满足。
结语:新课改下的高中数学课堂教学改革通过教学模式的转变,能够极大地提高学生的学习兴趣,增强自主学习的能力,提高课堂教学效率,使得高中数学教学再上一个新的台阶。

