基于行星排基本运动学关系式的传动比计算

李开龙



基于行星排基本运动学关系式的传动比计算

李开龙

（陆军装甲兵学院 蚌埠校区，安徽 蚌埠 233050）

利用简单行星排传动比计算式，导出行星排基本运动学关系式。对某型号坦克三自由度行星齿轮变速箱工作原理进行分析，揭示出三自由度行星齿轮变速箱可通过操纵元件的不同结合，实现不同的动力输出，通过利用行星排基本运动学关系式和行星齿轮变速箱中离合器的两两不同结合这个约束条件，对有关的行星排基本运动学关系式进行简化，从而比较容易地计算出七个前进挡和一个倒挡的传动比。

行星齿轮变速箱；传动；传动比

齿轮传动是机械设备、现代兵器、仪器和仪表中应用最广泛的机械传动形式之一[1]。行星传动能实现一自由度运动的固定轴齿轮机构不能实现的二自由度速度分解或合成[2]；多点啮合传递动力、传动时径向力平衡。坦克上采用行星齿轮传动的部件很多，如行星变速箱、行星转向机、行星侧减速器等。行星齿轮变速箱较定轴式齿轮变速箱具有结构紧凑、载荷容量大、传动效率高、齿间负荷小、结构刚性好、输入输出同轴线以及便于实现动力换挡与自动换挡等优点，在坦克装甲车辆获得了广泛的应用。行星变速机构的传动比可利用当量轮系法计算[3]，但方法较复杂，不易理解。根据行星排基本运动学关系式，再结合约束条件可很方便地计算出其不同动力输出时的传动比。

1 行星排基本运动学关系式

行星传动机构具有可绕中心轴周转的行星齿轮。行星齿轮联系着绕中心轴旋转的各元件，即太阳轮、齿圈和行星架，构成各种行星排。它既可单独应用为传动系中的差速器、功率分流或汇流机构并可作为减速器，又可串联为传动系中的增速、减速环节。若干行星排加上一些可控制的元件如制动器、离合器等，则可组成行星变速机构，行星变速机构以行星排为基本单元，图1是应用最广泛的内外啮合的齿圈式行星机构，也称为简单行星排机构。

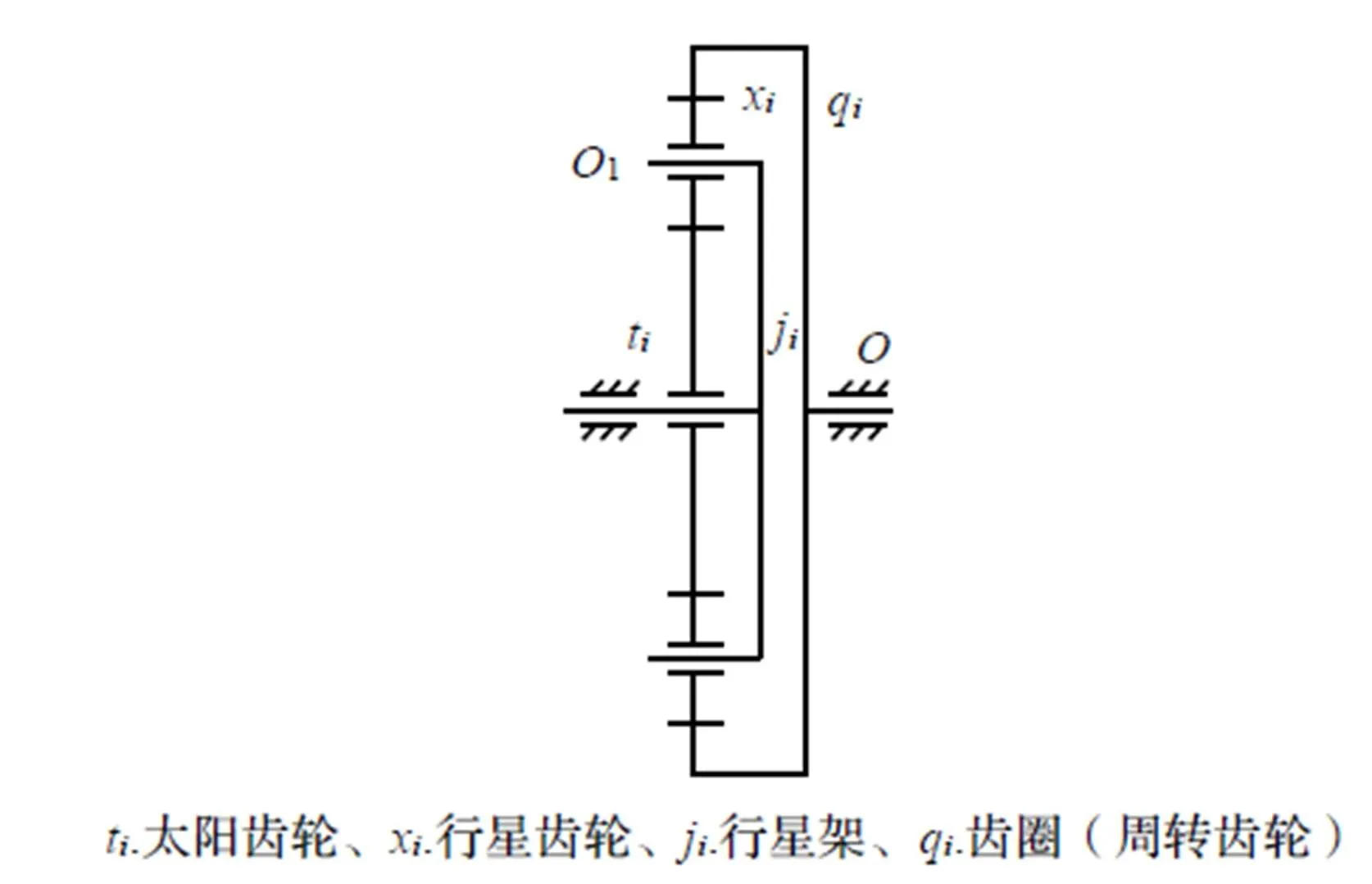
图1 简单行星排工作原理示意图

由行星轮系传动比计算式：

得其基本运动学关系式为：

式中：n、n、n分别为行星排太阳齿轮、齿圈、行星架的转速；k为行星排的特性参数；z、z分别为行星排齿圈和太阳齿轮的齿数。

2 三自由度行星变速箱传动比的计算

2.1 变速箱工作原理分析

图2是某型坦克变速箱的工作原理简图[4]，变速箱有7个构件，由四个行星排和六个离合器组成。动力由构件1输入，构件4输出。离合器C1、C4、C5、C6保证行星排元件制动，离合器C2、C3保证行星排闭锁，变速箱内离合器的两两不同结合，可实现七个前进挡和一个倒挡；以低速侧降一挡实现转向功能；空挡只结合一个操纵件。各行星排的组成如表1所示。各行星排的特性系数分别为1＝27/33＝0.818、2＝63/33＝1.909、3＝64/14＝4.517、4＝61/29＝2.103，变速箱各挡位的结合件如表2所示。

表1 各行星排的组成

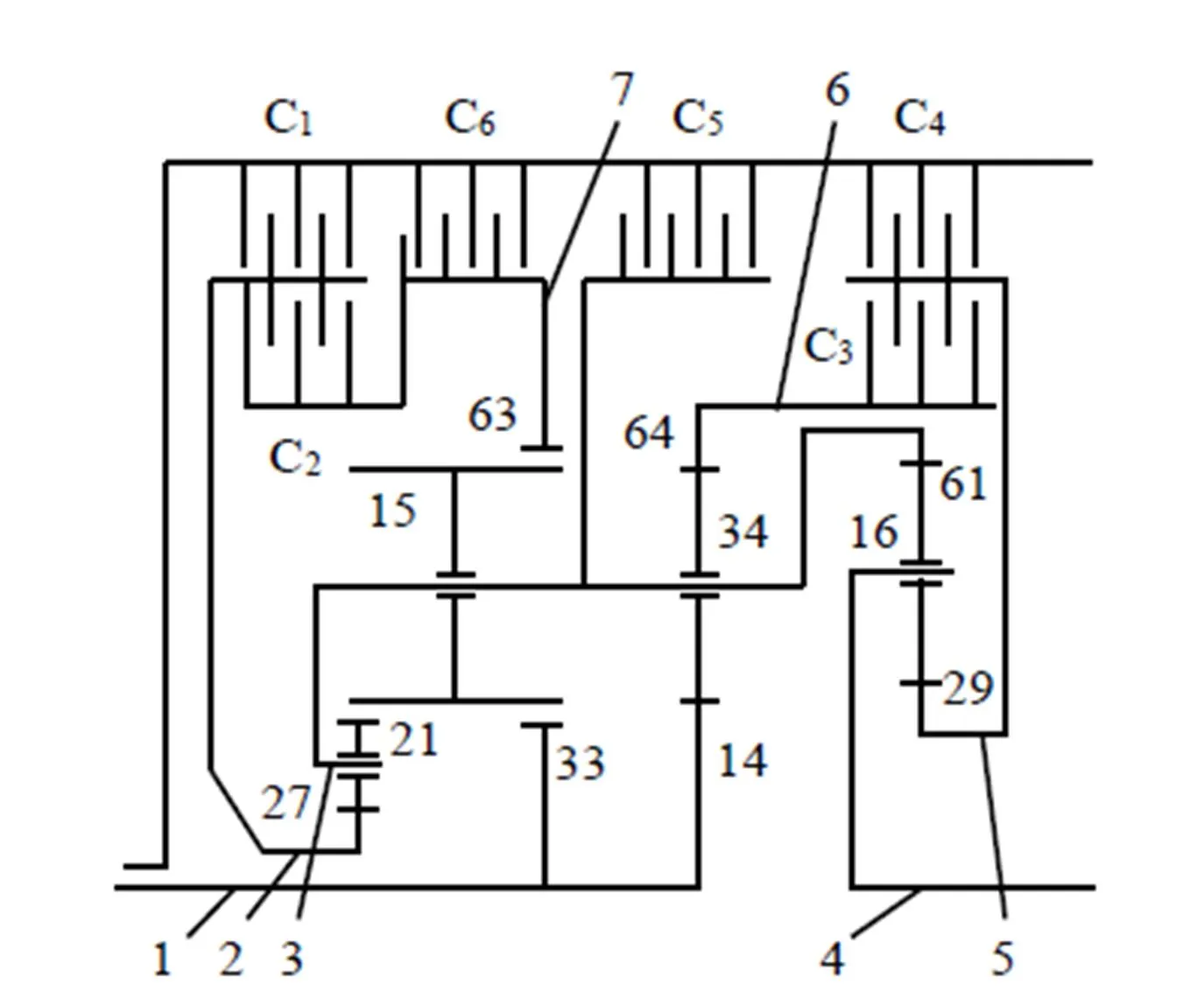
1.第一、二、三排的太阳轮 2.第一排的齿圈 3.第一、二、三排的行星架和第四排的齿圈 4.第四排的行星架 5.第四排的太阳轮 6.第三排的齿圈 7.第二排的齿圈 C1～C6.离合器

表2 变速箱各挡位的结合件

2.2 变速箱各挡位传动比计算

2.2.1 I挡传动比

C3C4结合时，由于第三排的齿圈和第四排的太阳轮被同时制动，则有n3＝n4＝0，又由于第四排的齿圈和第三排的行星架为同一构件，故n4＝n3。

故三、四行星排的运动学基本方程为：

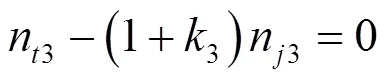
故I挡传动比为：

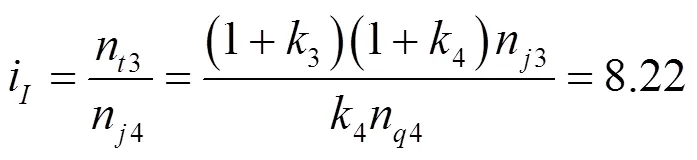
2.2.2 II挡传动比

C4C6结合时，第二排的齿圈和第四排的太阳轮被同时制动，则有n2＝n4＝0，又由于第四排的齿圈和第一、二、三排的行星架为同一构件，故n1＝n2＝n3＝n4。

故二、四行星排的运动学基本方程为：

故II挡传动比为：

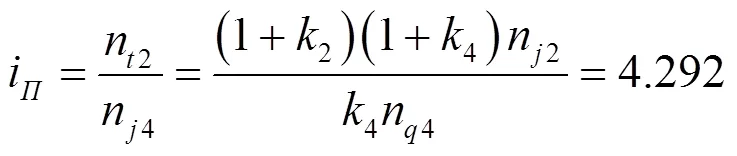
2.2.3 III挡传动比

C3C6结合时，第二排的齿圈被制动，第三排的齿圈和第四排的太阳轮成为一体，有n2＝0，n3＝n4，又有n1＝n2＝n3＝n4。

故二、三、四行星排的运动学基本方程为：

联立解得：

故III挡传动比为：

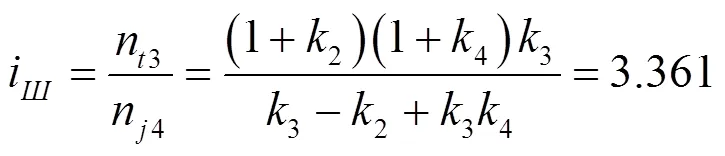
2.2.4 IV挡传动比

IV挡C1C4结合时，第一排的齿圈和第四排的太阳轮被同时制动，n1＝n4＝0。

故一、四行星排的运动学基本方程为：

故IV挡传动比为：

2.2.5 V挡传动比

V挡C1C3结合时，第一排的齿圈被制动，第三排的齿圈和第四排的太阳轮成为一体，n1＝0；n3＝n4。

此时第三和第四行星排的工作状态同三挡工作状态。

故V挡传传动比为：

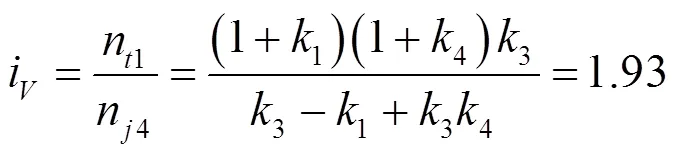
2.2.6 VI挡传动比

VI挡由于C2C4结合，第四排的太阳轮被制动n4＝0；第一排的齿圈和第二排的齿圈成为一体n1＝n2。因而，一、二、三行星排的运动学基本方程为：

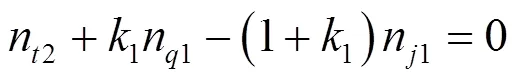
从而得出：

n1＝n1＝n1＝n2＝n2＝n2＝n3＝n3＝n3

即一、二、三行星排整体回转。

因为n3＝n4，故VI挡传动比为：

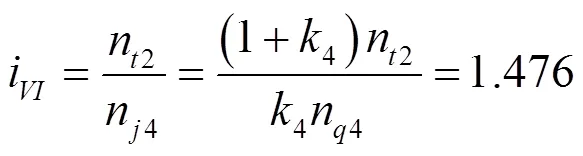
2.2.7 VII、倒挡传动比

VII挡C2C3结合时，n3＝n4。

倒挡C3C5结合时，n3＝n4；n1＝n2＝n3＝n4。

类似可分别列出有关行星排运动学基本方程，分别算出传动比。

3 结语

多自由度行星变速箱通常由多个单行星排组合而成，通过操纵元件的不同结合，可实现不同的动力输出，根据有关行星排运动学基本方程，结合约束条件可以很方便地计算出不同动力输出时的传动比，本方法对复杂的行星轮系传动比的计算有一定的参考价值。

[1]饶振钢. 行星传动机构设计[M]. 北京：国防工业出版社，1994.

[2]孙桓. 机械原理[M]. 北京：高等教育出版社，2001.

[3]刘东亚，等. 当量轮系法分析含有差动轮系的传动系统传动比[J]. 机械，2016（2）：66-69.

[4]汪仁和，等. 装甲兵新装备新技术介绍[M]. 蚌埠：装甲兵学院，2015.

The Calculation of the Transmission Ratio According to Basic Kinematics Relation for Planetary Gear Train

LI Kailong

(Bengbu Campus of Armored Institute of Chinese Army, Bengbu 233050, China )

The basic kinematics relation for planetary gear train was derived by using simple planetary transmission ratio calculation formula. The three degrees of freedom of planetary gear transmission working principle of a type tank was analyzed, which can complete different power outputs by manipulating different combination of components. By using basic kinematics relation and two different clutch combination of constraint conditions, basic kinematics relation for planetary gear train further simplified, thus more easily calculate the seven forward gears and one reverse gear transmission ratio.

planetary gear transmission；transmission；transmission ratio

U464.9

A

10.3969/j.issn.1006-0316.2018.11.006

1006－0316 (2018) 11－0024－04

2018－02－08

李开龙（1965－），安徽怀宁人，硕士，副教授，主要研究方向为机械设计与制造、计算机辅助设计、装甲装备模拟器的开发。