基于联合树的隐私高维数据发布方法
张啸剑 陈 莉 金凯忠 孟小峰
1(河南财经政法大学计算机与信息工程学院 郑州 450002) 2(河南财经政法大学网络信息安全研究所 郑州 450046) 3 (中国人民大学信息学院 北京 100872)
近年来,基于差分隐私的数据发布已成为隐私保护领域重要研究点.目前大多数研究均聚焦于低维数据或者一维数据的发布.高维数据在现实生活中普遍存在,例如个人购物数据、移动轨迹数据等.通过对这些高维数据发布与分析可以产生更加有意义的模式.由于高维数据通常蕴含大量个人隐私信息(例如购物记录中的敏感商品),直接发布将泄露个人敏感信息.然而如何在高维数据中得到统计结果的同时,又要保护原始数据隐私是个非常具有挑战性问题.其主要原因是随着维度与维度值域的增加,所形成的发布空间呈指数增长.例如设某数据集拥有1 000万条记录,每条记录的维度(或者属性)为10,每个维度有20个取值,对于全分布的域大小则有2010≈10TB个单元.如果直接利用噪音机制对10TB的输出单元添加噪音,则所需隐私预算、存储空间以及计算代价非常高.此外,每个单元的信息量非常小,假设1 000万条记录的大小为10 MB,则每个单元的真实信息量为10 MB/10TB=10-6.若设定隐私预算ε=0.01,利用拉普拉斯机制[1]产生的噪音约等于125(lap(1/0.01)≈125).如果直接为每个单元添加125大小的噪音,则该噪音值极大地扭曲了每个单元中的真实值(即125+10-6),发布结果的可用性极差.
目前已有少数基于概率图模型[2-3]、阈值过滤技术[4]以及投影技术[5]的高维数据发布方法,利用维度转换达到降维效果以及减少噪音对发布结果的影响,这些方法存在2个问题:
1) 文献[2-3]中的基于概率图模型方法通常利用指数机制[6]与稀疏向量[7]技术挑选属性关系对.然而,文献[2]中基于指数机制的属性对挑选方法受到候选空间大小的影响.如果候选空间非常大,所挑选的属性对越来越不准确,进而导致基于所选属性对构建的概率图不准确;文献[3]中采用稀疏向量技术挑选属性对,然而该技术并不满足差分隐私,进而导致文献[3]中整个高维数据发布方法不满足差分隐私.
2) 文献[4-5]中的基于阈值过滤与投影技术没有顾及到属性之间的依赖关系,利用阈值对维度直接截断达到降维效果.然而高维数据的属性之间普遍存在依赖关系,文献[4-5]中方法的实际可用性比较低.
总而言之,目前还没有一个行之有效的高维数据发布方法同时克服上述2种问题带来的不足.为此,本文基于联合树提出一种高效的高维数据发布技术.本文主要贡献包括3个方面:
1) 为了挑选出彼此关联的候选属性对,提出一种基于高通滤波的阈值过滤技术来缩减候选空间;
2) 结合缩减后的属性对候选空间,利用指数机制提出一种属性依赖图生成方法.结合属性依赖图,提出一种基于最大生成树技术的联合树生成方法.利用联合树推理出整体高维数据的联合分布,进而得到满足差分隐私的高维数据发布结果.
3) 理论证明所提出的高维数据发布方法满足ε-差分隐私.在5种真实数据集上进行了可用性评估实验.实验结果表明:PrivHD算法均优于PrivBayes与JTree算法.
1 相关工作
目前,基于差分隐私的高维数据发布方法主要分为2类:数据独立发布方法与数据相关发布方法.PriView[8]是数据独立发布方法的典型代表.该方法均等地处理所有的属性对,通过选择k(1 差分隐私保护模型[13-14]的精髓是确保在数据集中插入或者删除一条记录的操作不会影响任何计算的输出.相比于传统的隐私保护模型,差分隐私保护模型具有2个显著的特点:1)不依赖于攻击者的背景知识;2)具有严谨的统计学模型,能够提供可量化的隐私保证. 定义1. 设高维数据D与D′彼此相差1条记录,互为近邻关系.给定一个高维数据发布算法H,Range(H)为H的输出范围,若算法H在D和D′上 任意输出结果X∈Range(H)满足: Pr[H(D)=X]≤exp(ε)×Pr[H(D′)=X], (1) 则H满足ε-差分隐私.式(1)中,ε表示隐私预算,其值越小则算法H的隐私保护程度越高;Pr[H(D)=X]表示算法H基于D输出X的概率. 从定义1可以看出,ε-差分隐私限制了任意一个记录对算法H输出结果的影响.实现差分隐私保护需要噪音机制的介入,拉普拉斯机制[1]是实现差分隐私的主要技术.而所需要的噪音大小与其响应查询函数f的全局敏感性密切相关. 定义2. 设f为某一个查询,且f:D→d,f的全局敏感性为 (2) 其中,D与D′互为近邻,为映射的实数空间,d为f的查询维度. 文献[6]提出的拉普拉斯机制可以取得差分隐私保护效果,该机制利用拉普拉斯分布产生噪音,进而使得发布方法满足ε-差分隐私,如定理1所示. 定理1[6]. 设f为某个查询函数,且f:D→d,若方法H符合: H(D)=f(D)+ (3) 则H满足ε-差分隐私.式(2)中,lapi(Δfε)(1≤i≤d)为相互独立的拉普拉斯噪音变量,噪音量大小与Δf成正比、与ε成反比.因此,查询f的全局敏感性越大,所需的噪音越多. 文献[6]提出的指数机制主要处理抽样算法的输出为非数值型的结果.该机制的关键技术是如何设计打分函数u(ei).设H为指数机制下的某个隐私方法,则H在打分函数作用下的输出结果为 (4) 其中,Δu为打分函数u(ei)的全局敏感性,X为采用算法的输出域.由式(4)可知,ei的打分函数越高,被选择输出的概率越大. 给定高维数据集D,且D具有d个属性,即A={a1,a2,…,ad},每个属性的值域为Ωi(1≤i≤d).因此,整个值域的输出域为Ω1×Ω2×…×Ωd.在实际应用中,条件独立性在高维属性之间普遍存在,概率图模型是探索这种关系的主要技术,因此,本文采用联合树发掘低维属性构成的团和分割顶点的边缘分布,进而推理出来整体属性的联合分布.高维属性A的联合分布: (5) 其中,Pr(A)表示属性集合A的联合分布概率;T表示联合树,Ci表示T中第i个团,Pr(Ci)表示团Ci的边缘分布概率;Si j表示团Ci与团Cj之间的分割顶点,Pr(Si j)表示Si j的边缘分布概率. 采用Markov网表示属性对之间的关联关系,对Markov网进行三角化操作后获得团图.基于团图进行顶点消除来构建联合树.例如设A={a1,a2,a3,a4,a5,a6},结合A所对应的Markov网G如图1(a)所示,三角化操作结果如图1(b)所示.依据属性下标顺序进行顶点消除,所得到的联合树如图1(c)所示.由上述例子可以看出,结合联合树获得团和分割顶点的边缘分布之后,可以利用式(5)推理出整个高维属性的联合分布. 给定具有高维属性A的数据集D,结合属性集合A构建Markov网G.基于G构建联合树T,结合T生成团和分割顶点的边缘分布.基于式(5)生成属性A的联合分布Pr(A).为了使高维数据发布满足差分隐私,联合树的构建过程需要满足差分隐私.即:Markov网G的构建、团和分割顶点的边缘分布生成过程均需要满足差分隐私.因此,本文的问题是满足差分隐私的情况下如何发布比较精确的高维数据. 本节主要介绍PrivHD算法的概述以及该算法的具体实现细节,其中包括满足差分隐私的Markov网构建方法、Markov网的三角化方法、联合树的生成方法、边缘分布表的后置处理方法以及判断PrivHD算法是否满足ε-差分隐私. PrivHD算法利用Markov网对高维数据进行降维,利用满足差分隐私的联合树生成团和分割顶点的噪音边缘分布,最后生成合成高维数据集进行发布,该算法的描述如算法1所示: 算法1. PrivHD算法. 输入:高维数据集D、属性A={a1,a2,…,ad}、隐私预算ε; ①ε=ε1+ε2; ②G←Build-Noisy-MN(D,A,ε1);*生成噪音Markov网* ③T←Build-Noisy-JunctionTree(G,ε2); ④Pr(·)←Build-Noisy-Marginals(T); 给定一个具有高维属性A的数据集D和相应的参数,PrivHD算法首先利用Build-Noisy-MN方法生成满足差分隐私的噪音Markov网(行②).然后,通过对噪音Markov网三角化操作、完全团图构建操作,以及利用最大生成树方法生成联合树和团的边缘分布(行③).结合联合树所产生的团和分割顶点,生成每个团和分割顶点的边缘概率分布(行④).最后,通过对每个团的噪音边缘分布进行连接,生成最终的合成高维数据集进行发布. 结合属性集合构建Markov网G=(V,E),顶点集合V代表属性,边集合E代表2个属性之间的联系.本文利用互信息度量2个属性之间的关联性.给定属性ak,al,两者之间的互信息为I(ak,al): (6) 其中,i∈dom(ak),j∈dom(al),dom(ak),dom(al)分别表示属性ak和al的取值范围;Pr(ak=i,al=j)表示属性的联合分布,Pr(ak=i),Pr(al=j)分别表示ak与al的边缘分布. 由上述分析可知,G中2个属性的互信息决定着两者之间是否存在一条边.然而,计算2个属性之间的互信息是数据相关的,因此,需在满足差分隐私的情况下获得该信息.由于噪音机制的介入,首先需要计算出互信息的敏感度ΔI: (7) 其中,n=|D|. (8) 结合上述分析,Build-Noisy-MN的实现细节如算法2所示: 算法2. Build-Noisy-MN算法. 输入:高维数据集D、属性A={a1,a2,…,ad}、隐私预算ε1、过滤阈值θ; 输出:生成满足差分隐私的Markov网G. ①ε1=ε11+ε12; ②Eset←∅; ③ 初始化G=(V,E),V={a1,a2,…,ad},E←∅; ⑤ for each (ak,al) do ⑧Eset←Eset∪(ak,al); ⑨ endif ⑩ endfor 在Build-Noisy-MN算法中,行⑤~⑩部分实现对原始候选空间的压缩.获得候选边集合Eset后,利用指数机制挑选合适的边添加到G中(行~),进而形成满足差分隐私的Markov网G. 定理2. Build-Noisy-MN算法满足ε1-差分隐私. 证明. 给定2个近邻D与D′,令lap为噪音变量.给定一个属性对(ak,al),在D与D′上所对应的噪音互信息分别是: 根据上述推理过程可知不等式(9)与不等式(10)成立: (9) (10) 令M(Eset|D)表示在边集合Eset中选择边操作.根据指数机制以及不等式(9)和不等式(10)可证明不等式成立: (11) 根据不等式 可知,不等式(11)满足条件: (12) 证毕. 基于Markov网G的联合树构建通常包括G的三角化(如图1(b)所示)、生成完全团图、生成联合树3个过程.结合Build-Noisy-MN算法产生的Markov网G,三角化操作过程如算法3所示: 算法3.Triangulation-Partition算法. 输入:Markov网G=(V,E)、顶点消除顺序φ; 输出:包含所有团的集合CL、三角化后Markov网. ①G′←G,CL←∅; ② for each nodeu∈φdo ③ if不存在边(v1,v2)∈neibors(u) then ④ (v1,v2).mark=true; ⑤G′.E←G′.E∪(v1,v2); ⑥ endif ⑦C←neibors(u)∪u;*根据顶点消除顺序找团* ⑧CL←CL∪C; ⑨ endfor ⑩ returnG′,CL. 在Triangulation-Partition算法中,行②~⑨是根据顶点消除顺序寻找所有团的过程.Markov网G=(V,E)中的团是一个顶点子集,其中每一对顶点之间均有一条边相连,即一个团是G的一个完全子图.例如给定φ={a1,a2,a3,a4,a5,a6},按照所设定的顶点消除顺序,所形成的如图1(b)所示.所形成的团分别是C1={a1,a3,a5},C2={a2,a5},C3={a3,a4,a5},C4={a4,a5,a6}.行③~⑥是对G三角化的过程.所谓三角化操作是对所有长度大于3的环引入弦的过程.例如,图1(b)中虚线即为三角化后的弦. 根据所获得的团构建完全团图CG=(CL,E),其中CL表示所有团的集合,E表示团之间存在的边.每一条边(Ci,Cj)∈E,都有一个权重w(Ci,Cj),并且w(Ci,Cj)=size(Ci∩Cj).即2个团的交集大小为边的权重.例如根据Triangulation-Partition算法获得CL={C1,C2,C3,C4},相应的权重分别为w(C1,C2)=1,w(C1,C3)=2,w(C1,C4)=1,w(C2,C3)=1,w(C2,C4)=1,w(C3,C4)=2,所产生的完全团图如图2(a)所示: Fig. 2 Construction of junction tree on complete clique graph图2 基于完全团图的联合树构建 结合上述生成的完全团图CG构建联合树.构建联合树的性能瓶颈在于团的大小,而基于最小数量的团构建联合树是个NP难问题.因此,本文基于CG设计一种类似于最大生成树的贪心算法,具体细节如算法4所示: 算法4. Build-Noisy-JunctionTree算法. 输入:完全团图CG=(CL,E)、隐私预算ε2; 输出:联合树T. ①T=(V,E); ②T.V←∅,T.E←∅; ③visited(CG.E)=false;*CG的边均未被访问过* ④T.V←C,C∈CG.CL;*选择最大的团* ⑤m←size(CG.CL);*m为CG中团的个数* ⑥noisy-count(Tab(C)←count(Tab(C))+lap(mε2)*Tab(C)表示团C的边缘分布表* ⑦ whileT.V≠CG.CLdo*构建联合树* ⑧ for each (Ci,Cj)∈CG.Eandvisited(Ci,Cj)=false do ⑨ (Ck,Cl)←max(w(Ci,Cj));*选择权重最大的边* ⑩ ifCk∈T.VandCl∉T.Vthen count(Tab(Cl))+lap(mε2); 在Build-Noisy-JunctionTree算法中,首先选择CG中规模最大的团开始联合树的构建(行④).针对所挑选的团,构建该团的边缘分布表,利用拉普拉斯机制对该表添加噪音(行⑤~⑥).在行⑧~的for循环中,先选择权重最大的边,再判断团Ck与Cl是否分别满足条件.如果是,把团Cl添加联合树的顶点集合中,把边(Ck,Cl)添加联合树的边集合中.对于贪心搜索到的团Cl,利用拉普拉斯机制对其边缘分布表添加噪音(行).例如CL={C1,C2,C3,C4}.选择C3={a3,a4,a5}作为开始顶点,以最大生成树方法贪心地生成联合树,如图2(b)所示,使得最终的权重之和最大. 定理3. Build-Noisy-JunctionTree算法满足ε2-差分隐私. 证明. 由Build-Noisy-JunctionTree算法可知,产生m个团之后,分别对这些团添加独立的拉普拉斯噪音.在原始数据D中去掉或者添加1条记录,最多影响m个团的计数,因此,为每个团添加噪音的大小为lap(mε2).根据定理1和差分隐私序列组合性质可知,Build-Noisy-JunctionTree算法满足ε2-差分隐私. 证毕. 由Build-Noisy-JunctionTree算法中的行⑥与行可知,最终形成的联合分布精度如何,直接受到联合树T中团个数m的约束.如果采用噪音方差(2(Δfε2)2)度量每个团产生的误差,则m个团产生的误差总和: (13) 其中,Ωj表示属性aj的值域,|Ωj|表示该值域大小. 例如由图2(b)可知CL={C1,C2,C3,C4},即m=4.设置A中6个属性的值域大小分别为{2,2,3,3,2,2}.根据式(13)可知Lerror(CL)=2304 由式(13)可知,每个团的边缘分布表噪音误差的高低直接与团的个数m相关,m越少最终的联合分布越精确.Triangulation-Partition算法产生的团通常只包含3个属性顶点,而仔细观察可以发现,该算法的三角化操作并不充分,而三角化操作要求所有长度大于3的环均要引入弦.为此,本文设计一种Bigger-Clique算法来构建更大的团图,具体细节如算法5所示: 算法5. Bigger-Clique算法. 输入:由Triangulation-Partition算法产生的G′=(V,E); 输出:包含所有团的集合CL. ①VS←∅,UV←G′.V;*VS表示访问过的顶点集合,UV表示未被访问过的顶点集合* ②max_label=1; ③ 随机选择一个顶点u∈G′.V,labeled(u)=max_label; ④VS←VS∪u; ⑤UV←UV-u; ⑥ whileUV≠∅ do ⑦ for eachv∈G′.Vandv∈neibors(VS) do ⑧n_v←max_labeled_neibors(v); ⑨labeled(n_v)←max_label+1; ⑩ endfor 例如在图3(a)所示的Markov网中,为了充分三角化操作,顶点a6与顶点a3之间也引入了弦.依据顶点消除顺序 ,获得更大的团{a3,a4,a5,a6}.最终形成的团CL={C1={a1,a3,a5},C2={a2,a5},C3={a3,a4,a5,a6}},此时m=3.根据式(13)可知Lerror(CL)=1296相比2304充分三角化操作能够比较明显地降低噪音误差.然后利用Build-Noisy-JunctionTree算法获得的联合树如图3(b)所示. Fig. 3 Construction of junction tree on bigger complete graph图3 基于更大完全团图的联合树构建 由Build-Noisy-JunctionTree算法行⑥与行可知,对每一个团的边缘分布表均添加lap(mε2),进而保证每个边缘分布表满足差分隐私.根据联合树的执行相交性质(如性质1)可知,对于任意分割顶点Si j,则满足Si j=Ci∩Cj.因此,对于联合树中的任意分割顶点,通过团边缘分布表投影的方法可以获得它们的噪音边缘分布表.当获得所有团和所有分割顶点的边缘分布之后,利用式(5)可以计算出所有属性的联合分布Pr(A). 性质1. 执行相交性质.给定1棵联合树T以及T中任意顶点对Ci与Cj,如果有变量X满足X∈Ci∩Cj,则X也在Ci与Cj之间唯一路径的每个顶点中.那么T具有执行相交性质. 例如在图2(b)中获得Tab(C2={a5,a2})和Tab(C3={a5,a4,a3})之后,通过投影可以获得分割顶点{a5}的边缘分布.假设a2,a3,a4,a5均为二进制属性,相应的噪音边缘分布如图4中(a)部分与图4中(c)部分所示.由于分割顶点{a5}=C2∩C3,可以利用团C2或者团C3来获得{a5}的边缘分布.然而,通过图4中(b)部分与图4中(d)部分的噪音值ncnt可以发现,分割顶点{a5}在团C2与团C3中获得的边缘分布互相不一致.而互不一致性直接导致最终所有属性的联合分布不准确.为了处理这种不一致性,本文基于文献[3,8,15]中的互一致性方法来后置处理团和分割顶点上的边缘分布不一致性. Fig. 4 Mutual consistency processing on clique and separator图4 团与分割顶点的互一致性处理 设Tab(C1),Tab(C2),…,Tab(Ck)为团C1,C2…,Ck所对应的噪音边缘分布表.令I=C1∩C2∩…∩Ck.后置处理的目标是对于任意2个团Cx,Cy∈{C1,C2,…,Ck},使得TabCx(i)=TabCy(i)成立,其中i是I值域中一个可能的取值.令ccntI(i)表示I经过处理后的噪音计数(例如图4(b)中ccnt的值).ccntI(i)表示形式为 (14) 其中,Ij表示Cl中除I之外的属性,|Ωj|表示Ij的值域大小. 例如给定团C2={a2,a5}和团C3={a3,a4,a5},以及二者的交集I={a5},假设a2,a3,a4,a5均为二进制属性.TabC2(i=0)=4,TabC2(i=1)=5(如图4中(b)部分中的ncnt所示),TabC3(i=0)=6,TabC3(i=1)=7(如图4中(d)部分中的ncnt所示).利用式(14)可以计算出ccntI(i=0)=4.33,ccntI(i=1)=5.67(如图4中(b)部分和图4中(d)部分所示). 利用式(14)可以获得I在C1,C2…,Ck中的一致性值.接下来是根据ccntI(i)来调整团C1,C2…,Ck中的ncnt值进行调整.令ccntCl(c|i)表示I取值为i时团Cl的后置处理值,具体表示形式为 (15) 例如给定团C2,C3,其边缘分布表如图4中(a)部分与图4中(c)部分所示.由式(15)可知ccntC2(C1|i=0)=1.33,ccntC2(C2|i=0)=3.33,ccntC2(C1|i=1)=2.34,ccntC2(C2|i=1)=3.34,具体结果如图4中(a)部分所示.同理可以对图4中(c)部分中的ncnt值进行调整. 因此,根据式(14)和式(15)可以对团和分割顶点的边缘分布表进行一系列后置处理.然而在调整过程中,后置处理后的值有可能发生冲突.例如,C1∩C3={a3,a5},C3∩C4={a4,a5}.如果第1步先对团C1和C3进行一致性处理,则Tab(C1)和Tab(C3)在属性{a4,a5}达成一致性.第2步对团C3和C4一致性处理,则Tab(C3)和Tab(C4)在属性{a4,a5}达成一致性.然而,第2步的一致性处理可能导致第1步中计数的不一致性,其原因是C3和C4一致性处理改变了{a5}的分布.如果首先C1∩C3∩C4在{a5}上进行了互一致性处理,则第2步不会改变第1步中的一致性结果[2]. 根据上述的例子可知,互一致性处理的先后顺序至关重要.因此,本文结合分割顶点上存在的偏斜关系给出一个全序的拓扑序列,进而获得互一致性处理的先后关系.令S={s1,s2,…,sk}为部分分割顶点的集合,根据S上的偏序关系S,≼形成哈斯图,然而结合哈斯图进行拓扑排序.本文利用分割顶点之间的覆盖关系表示≼.对于任意2个分割顶点si与sj,若sj覆盖si,则sisj∧∃sl(sl∈S∧sislsj)成立.sj覆盖si使得si与sj之间存在一条无向边,且si在sj的下方. 例如根据图2(b)所示,S={{a5},{a3,a5},{a4,a5}},根据S,≼所形成的哈斯图如图5所示: Fig. 5 Construction of Hasse diagram图5 哈斯图构建 定理4. PrivHD算法满足ε-差分隐私. 证明. 在PrivHD算法中,行②利用指数机制挑选属性对来形成Markov网,定理3已证明该步骤满足ε1-差分隐私.行③利用拉普拉斯机制为每个团的边缘分布表添加噪音,根据定理1与定理4可知,行③满足满足ε2-差分隐私.根据定理6差分隐私的顺序组合性质可知,PrivHD满足(ε1+ε2)-差分隐私.由于ε=ε1+ε2,则PrivHD算法满足ε-差分隐私. 证毕. 为了对PrivHD算法的可用性进行分析,本节将通过具体的实验进行验证与说明.实验平台是4核Intel i7-4790 CPU(4 GHz),8 GB内存,Windows 7操作系统,部分实验在Intel E5-2600 CPU,32 GB内存,Linux平台上运行.所涉及代码用R语言及Matlab实现.实验所采用的5个数据集BR2000,Adult,NLTCS,TPC-E,TIC均被广泛使用于高维数据发布.其中BR2000来自于2000年巴西全国人口普查数据,该数据包含38 000条记录;Adult源自于美国人口普查中心,包含45 222条个人信息;NLTCS源自于美国护理调查中心,记录了21 574名残疾人不同时间段的日常活动;TPC-E来自于TPC开发的在线事务处理程序,记录了包含交易、交易类型、证券、证券状态等信息的40 000条数据;TIC为Coil网站数据分析竞赛所用数据集,记录了某保险公司包括客户购买产品信息以及客户社交信息在内的98 220条信息.数据集的具体细节如表1所示: Table 1 Description of Five Datasets表1 5种数据集信息描述 结合上述5种数据集,分别用k-way查询与SVM分类度量PrivHD,PrivBayes,JTree算法发布高维数据的准确性与可用性.k-way查询k的取值为2,3,5,6,并使用平均方差(average variation)度量查询结果的准确性;在合成数据集上构建SVM分类模型并做出预测,使用误分类率(misclassification rate)度量分类结果的准确性.隐私预算参数ε的取值为0.05,0.1,0.2,0.4,0.8,1.6.分配策略为ε1=0.1,ε2=ε-0.1,即隐私预算ε1=0.1用于构建联合树,剩余的隐私预算用于产生噪音边缘分布,当ε取值为0.05,0.1时,ε1=12ε,ε2=12ε.每个算法重复实验50次,取度量指标的平均值作为实验结果. 1) 基于参数ε和k-way查询范围的变化,对比PrivHD,PrivBayes,JTree算法的k-way查询结果. 由图6可发现,在大多数情况下,PrivHD优于JTree和PrivBayes,在ε<0.2的情况下,PrivBayes的平均方差是PrivHD的2倍多.尤其是k=5或6的情况下,PrivHD明显优于JTree和PrivBayes,在维度比较大的TPC-E数据集上,JTree的平均方差是PrivHD的1倍多.在维度很大的TIC数据集上,由于PrivHD采用基于更大团的联合树构建方法的缘故,其平均方差同样小于JTree和PrivBayes,尤其是在k=5或k=6的情况下,PrivBayes的平均方差最坏情况下大概是PrivHD的1倍多. Fig. 6 Result of k-way marginals on five datasets图6 5种数据集下k-way查询结果 k-way查询的平均方差值越小表示发布高维数据的可用性越高,随着k值的增大,3种算法的平均方差也越来越大,其原因是较大的k-way查询会造成拉普拉斯噪音的累积,进而造成可用性降低.但是在较大的k-way查询下,PrivHD的表现仍然好于JTree和PrivBayes,其原因是PrivHD采用了更优的联合树构建方法以及后置处理技术,进一步说明了PrivHD的高可用性.在数据集维度较低的NLTCS数据集上,PrivHD表现仍好于JTree,PrivBayes,而3种算法差别不大的原因是NLTCS数据集维度比较小,且为二进制数据. 2) 基于参数ε的变化,对比PrivHD,PrivBayes,JTree,NoPrivacy算法的SVM分类结果. 本组实验在Adult,NLTCS和TIC数据集上进行分析.首先分别根据PrivHD,PrivBayes,JTree算法产生合成数据集,然后在合成数据集上构建SVM分类模型.对于Adult数据集,依据某个人:1)是否是男性(如图7(b)中Y=gender);2)是否有大专学位;3)年薪是否大于5万;4)是否已婚做出预测.对于NLTCS数据集,依据某个人:1)是否能够外出;2)是否能够管理资金;3)是否能够游泳;4)是否能够旅行做出预测.对于TIC数据集,依据某个人:1)是否拥有轿车;2)是否拥有房子;3)家庭平均年收入是否大于3万;4)是否已婚做出预测.其中NoPrivacy算法是在原始数据集上构建SVM分类模型并做出预测.本文将数据的20%作为测试集,将80%作为训练集. Fig. 7 Result of SVM classifiers on three datasets 由图7可以发现,PrivHD算法的SVM分类结果优于JTree和PrivBayes算法,在Adult数据集上,最坏情况下,PrivBayes的误分类率是PrivHD的将近3倍,JTree的误分类率也明显高于PrivHD.在数据维度很高的TIC数据集上,PrivBayes和JTree的误分类率同样高于PrivHD.随着参数ε从0.05变化到1.6,PrivHD,JTree,PrivBayes算法的误分类率在相应降低,其原因是小的ε值会引入更多的拉普拉斯噪音,进而增加拉普拉斯误差. 针对差分隐私行下高维数据发布问题,本文首先对现有高维数据发布方法进行分析,并在此基础上提出基于联合树的发布算法PrivHD,引入满足差分隐私的高通滤波与后置机制.在过滤的基础上提出了基于指数机制的Markov网构建方法以及基于最大生成树的联合树构建方法.从理论角度进行对比分析的结果显示,PrivHD优于同类算法.最后,通过真实数据集的实验结果表明PrivHD能够在满足差分隐私的同时输出比较精确的k-way查询与SVM分类结果.今后的工作需要考虑在数据流环境中发布高维数据.2 定义与问题
2.1 差分隐私
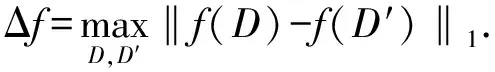
[lap1(Δfε),lap2(Δfε),…,lapd(Δfε)],
2.2 联合树
2.3 问题描述
3 基于联合树的精确发布方法
3.1 PrivHD算法概述
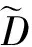

3.2 Build-Noisy-MN算法

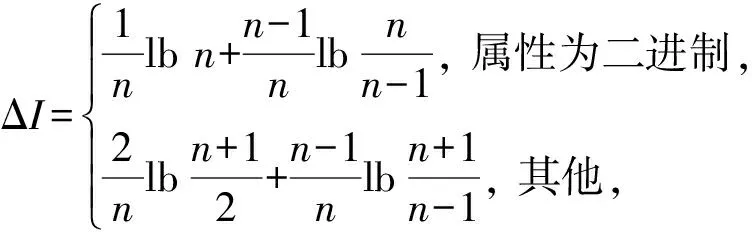

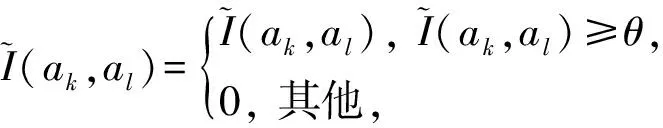


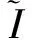



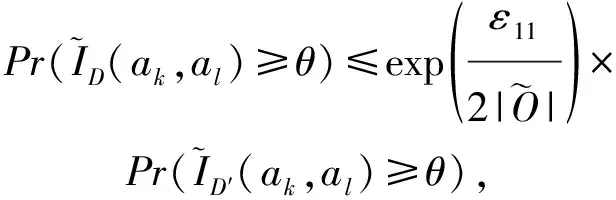
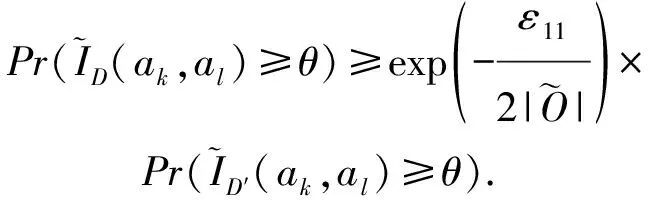
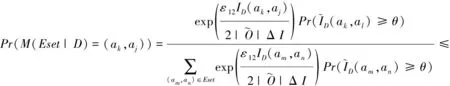

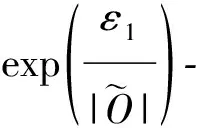
3.3 Build-Noisy-JunctionTree算法


3.4 Build-Noisy-Marginals算法

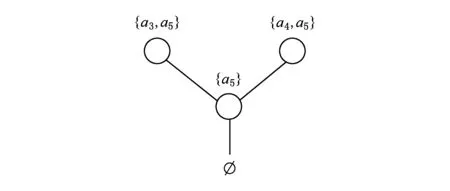
3.5 Clique-Join算法
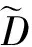
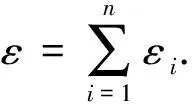
4 实验结果与分析
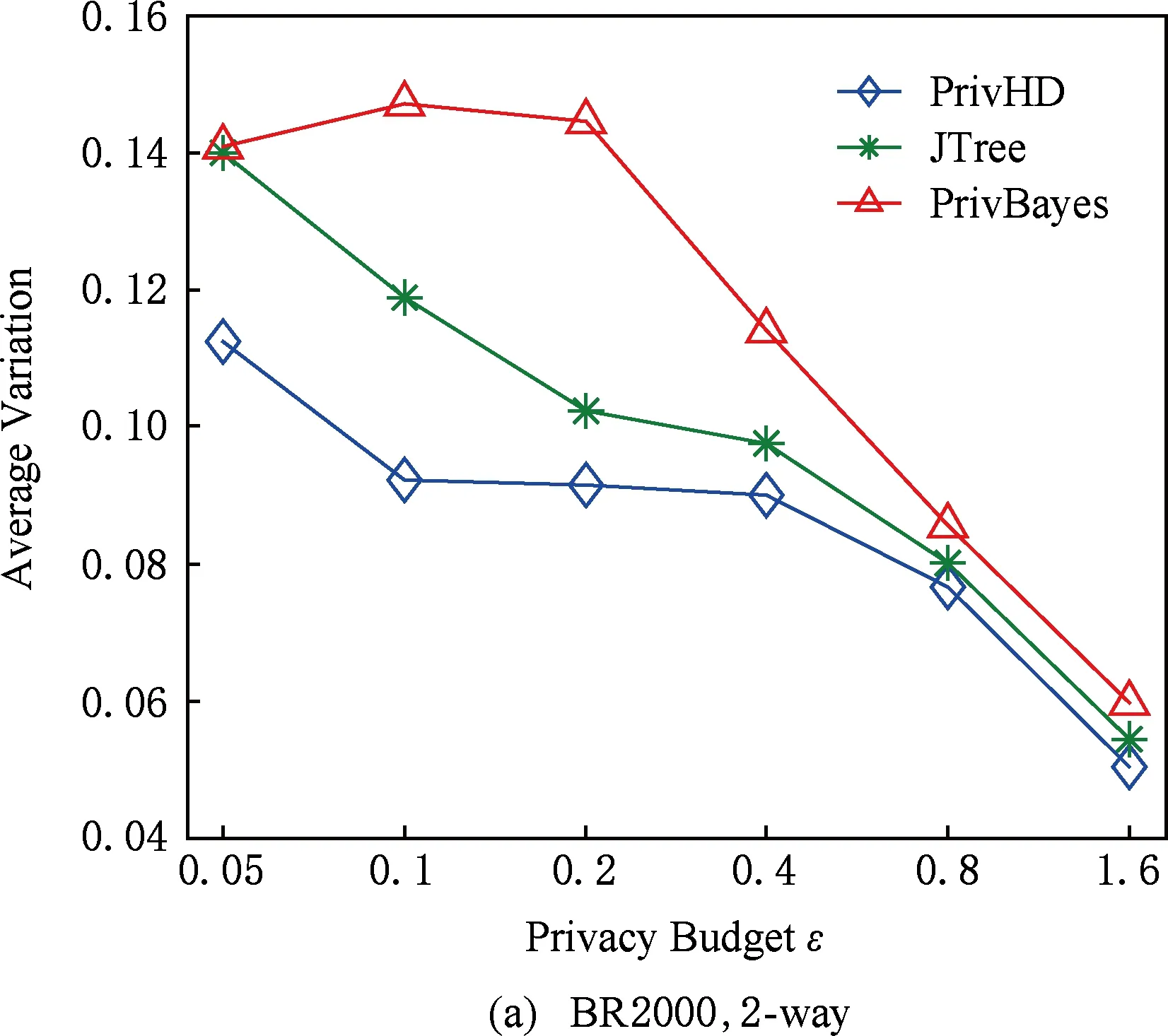
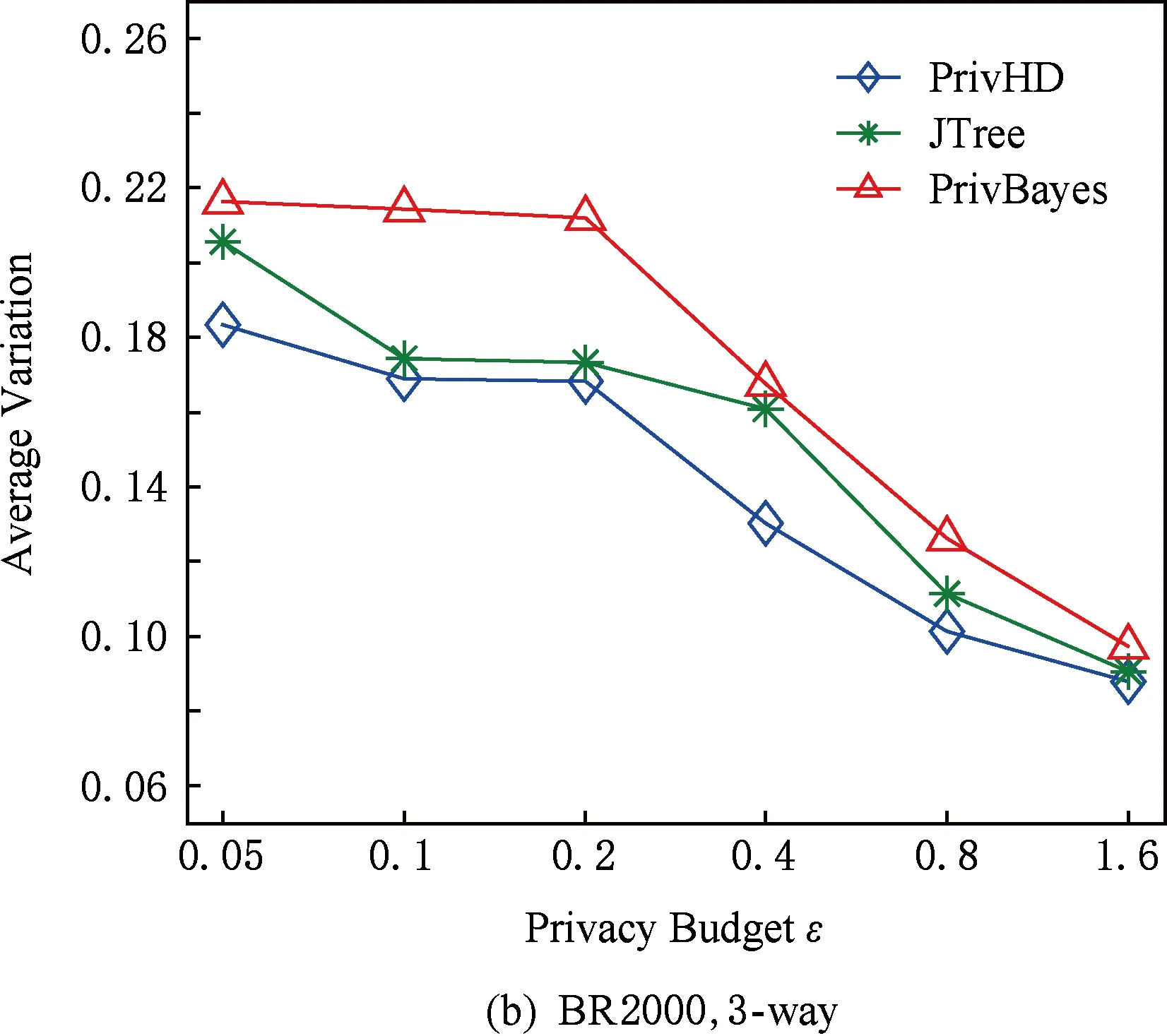




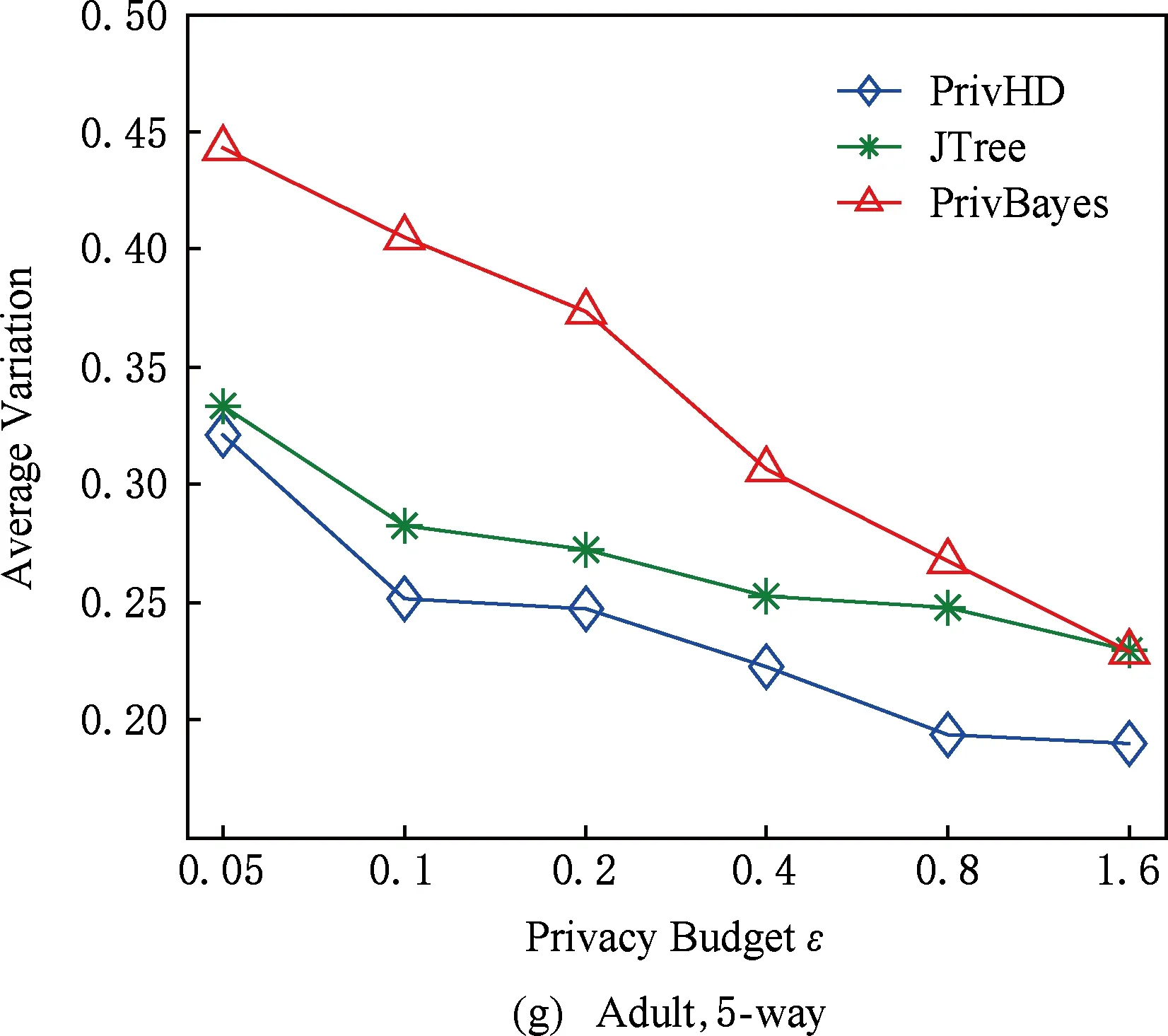


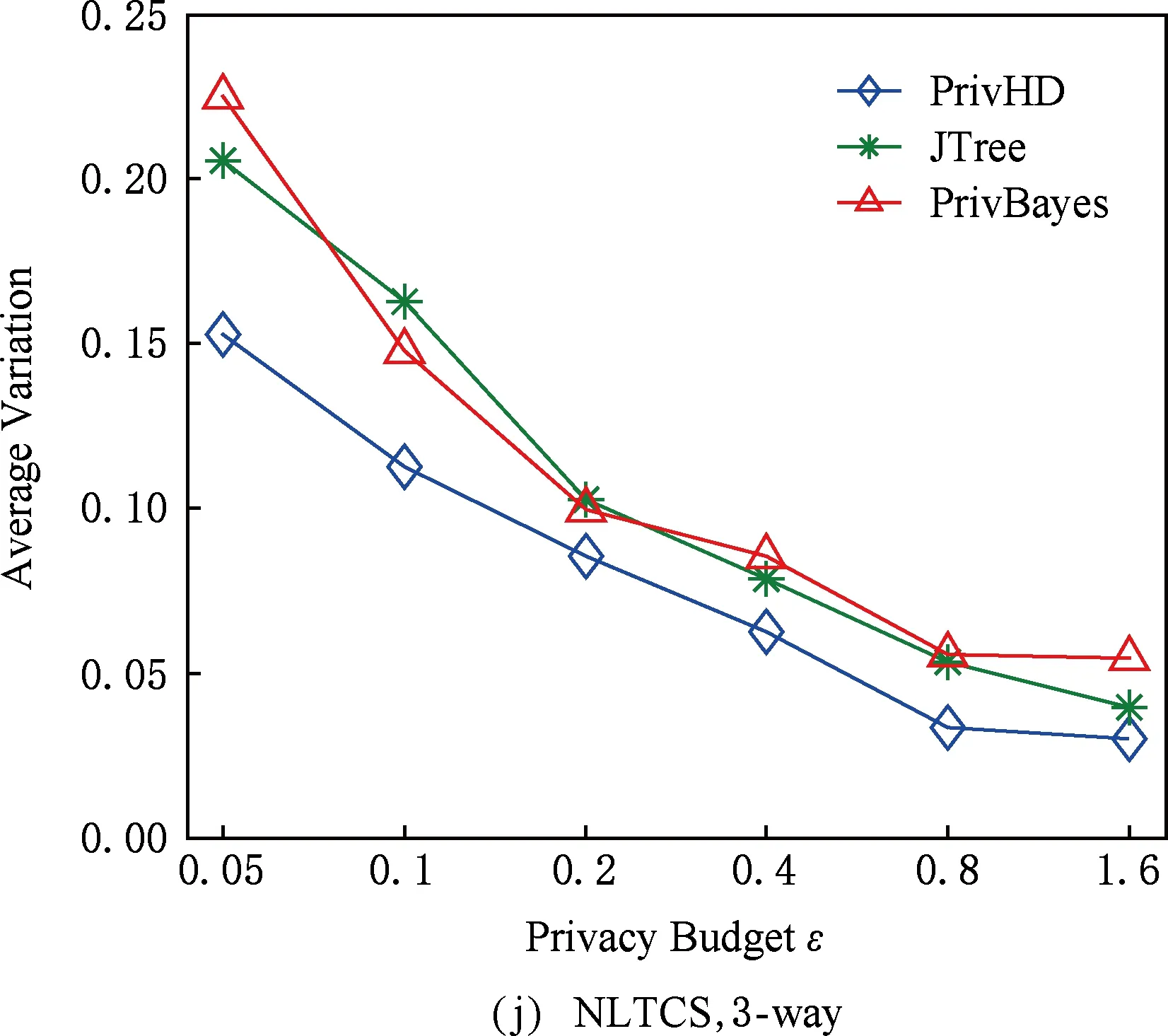
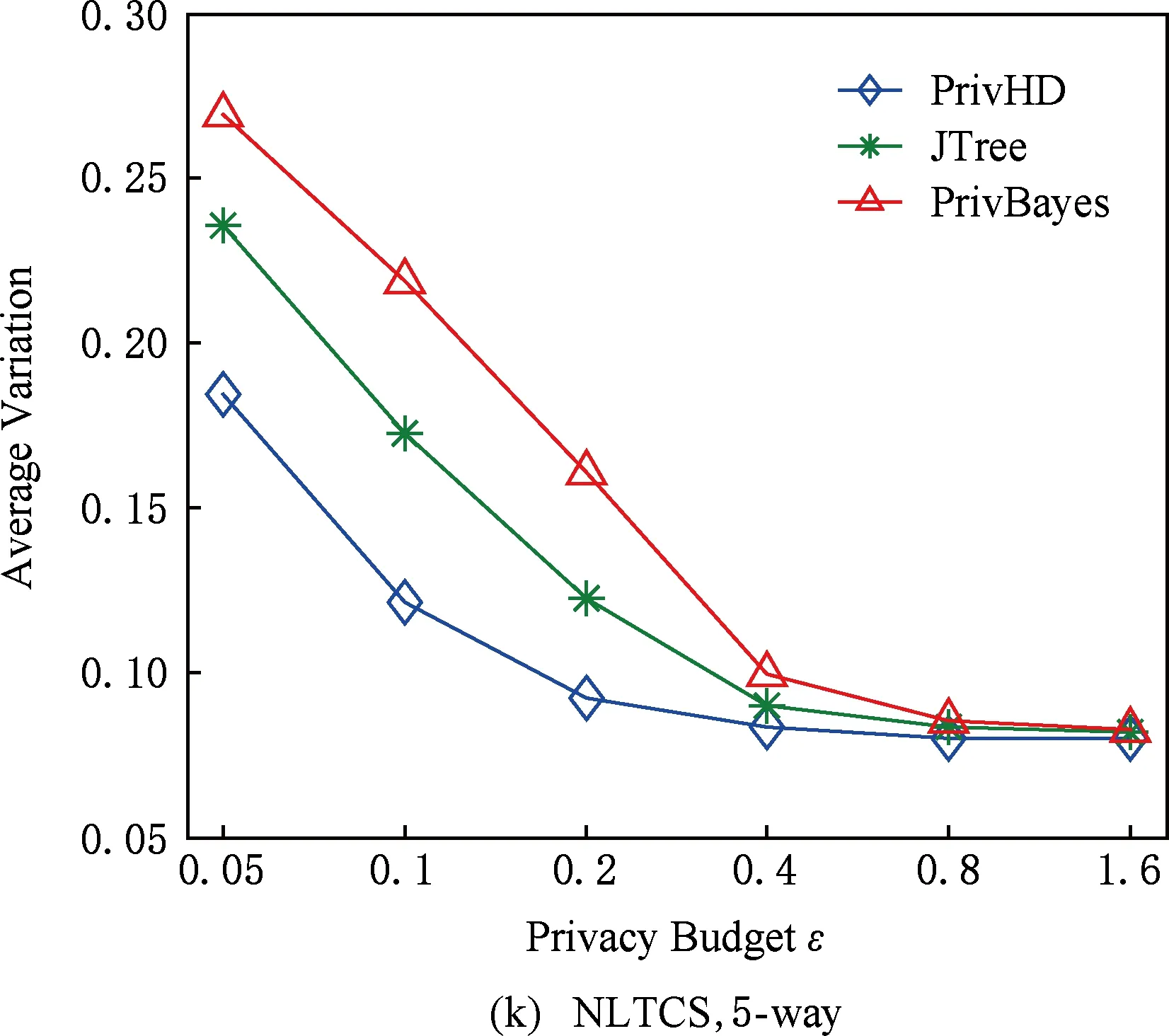
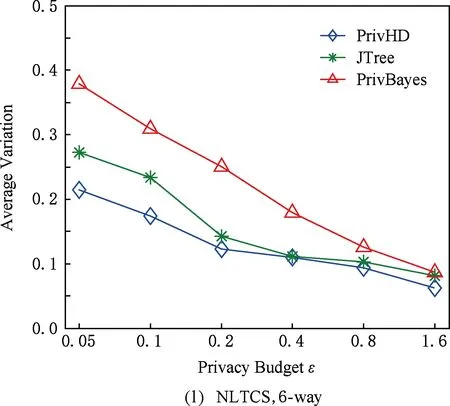

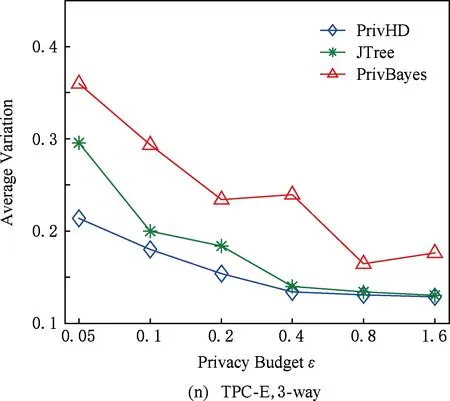
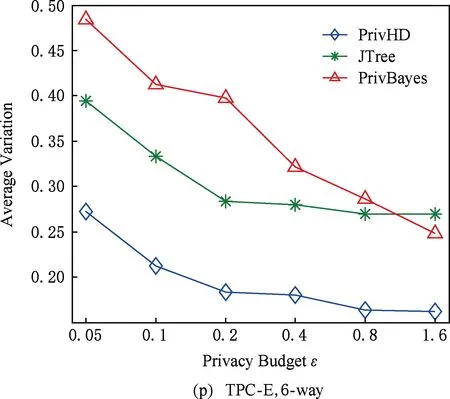

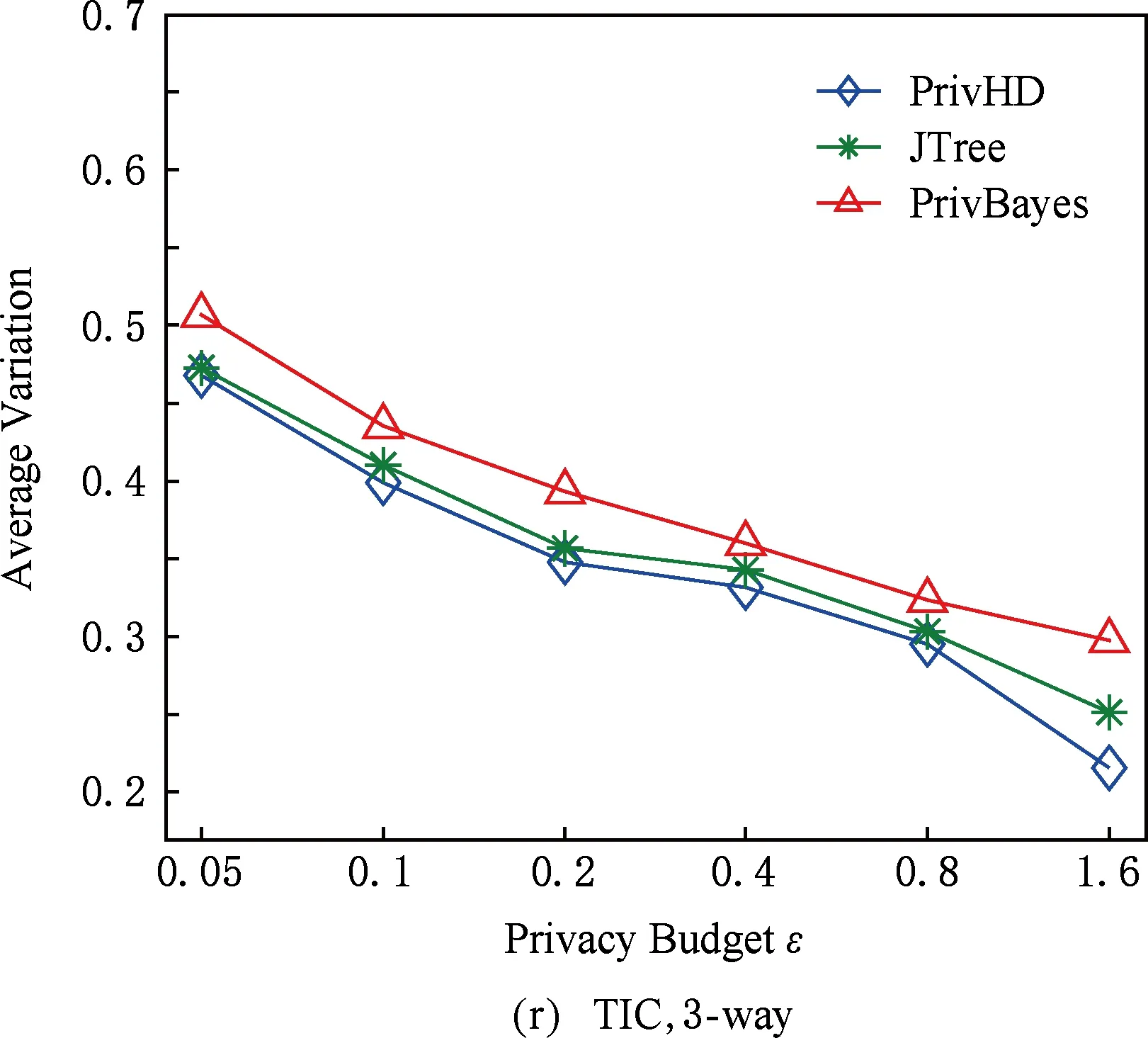

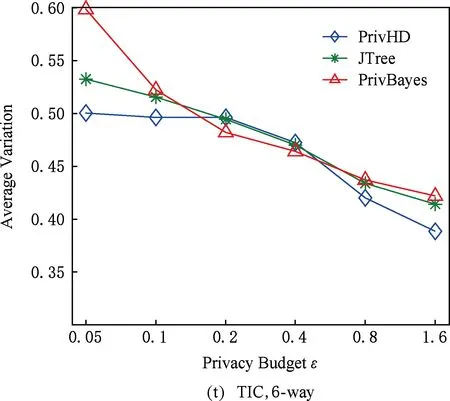










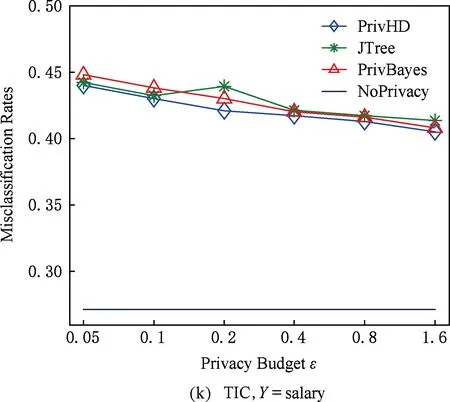

图7 3种数据集下SVM分类结果5 结束语

