一种线性的在线AUC优化方法

朱真峰 翟艳祥 叶阳东

(郑州大学信息工程学院 郑州 450052)

AUC(area under the ROC curve)[1]是衡量分类算法性能的重要指标之一，被广泛应用于不平衡类的学习、代价敏感学习、排序学习和异常检测等[2-5].AUC值难以精确计算，通常采用参数假定、半参数假定或非参数假定方法进行估计.机器学习领域常用非参数假定方法，其估计在数值上等价于排序的WMW(Wilcoxon-Mann-Whitney)统计[6].设计分类算法通常需要将评价指标作为优化目标，使算法的优化目标与性能评价指标一致，以期获得理想的性能.基于AUC评价指标，研究者提出诸多直接优化AUC的批处理算法[7-11]，这类算法假设学习之前已经得到全部训练数据.

在线学习凭借其处理大规模数据和流数据的高效性，在机器学习领域受到广泛关注[12-18].传统在线学习方法的目标函数仅需考虑由单个训练样本构成的损失函数之和;而AUC优化的目标函数来自不同类别的样本对构成的损失函数之和，与训练样本数呈二次增长关系.直接将传统在线学习方法应用于AUC优化问题，需要存储所有历史(旧)样本，这对于大数据分析是不可行的.

为了实现在线AUC优化，研究者提出了多种以AUC为优化目标的在线学习方法[19-23].这些方法可以分为2类：缓冲方法和统计方法.缓冲方法基于缓冲采样思想，构建2个固定大小的缓冲，分别存储采样的正负旧样本[19-21]，把接收的新样本存储在相应的缓冲中；如果缓冲满，采用蓄水池抽样(reservoir sampling)或先进先出(fist-in-first-out)策略，以新样本替换相应缓冲中的旧样本，并用新样本与另一个缓冲中的所有样本构成的损失函数代表新样本与另一类的所有旧样本构成的损失函数进行计算，更新模型.统计方法通过存储和更新一阶统计量(平均值)和二阶统计量(协方差矩阵)，利用随机梯度下降方法[22]或者AdaGrad方法[23]实现在线AUC优化；每次迭代的梯度由新样本与另一类的所有旧样本的平均值和协方差矩阵计算得到.

上述2类方法都是通过在求解过程中避免直接计算所有的损失函数，以减小问题的规模.不同之处在于，缓冲方法需要存储并不断地扫描缓冲中的样本，算法的空间复杂度和每次迭代的时间复杂度与缓冲大小呈正比关系.统计方法不需要存储任何旧样本，只需要扫描一遍训练集，其存储规模独立于训练样本个数；统计方法涉及协方差矩阵的存储和计算，相应算法的空间复杂度和每次迭代的时间复杂度与样本维数平方呈正比关系，高于传统在线梯度下降算法[12]、与ONS(online Newton step)[16]相同.

如何使AUC优化的目标函数不再和训练样本数二次相关、仅与训练样本数线性相关是一个值得研究的问题.本文在深入研究现有AUC优化算法的基础上，提出了一种与训练样本数线性相关的目标函数；理论推导证明了最小化该目标函数等价于最小化由L2正则化项和最小二乘损失函数组成的AUC优化的目标函数.基于该目标函数，本文提出了线性的在线AUC优化(linear online AUC maximization， LOAM)方法，并根据不同的分类器更新策略，给出2种算法：1)采用增量式最小二乘法(incremental least squares classifier， ILSC)[24-25]更新分类器的LOAMILSC算法；2)采用AdaGrad方法[17,23]更新分类器的LOAMAda算法.其中，LOAMILSC算法的空间复杂度和每次迭代的时间复杂度与ILSC算法相同，LOAMAda算法的空间复杂度和每次迭代的时间复杂度与传统在线梯度下降算法相同；这2种算法都仅需扫描一遍训练集，不需要存储任何旧样本.本文通过大量的实验验证了所提算法的有效性.

1 AUC优化问题

给定一个独立同分布的二分类训练样本集X={(xi,yi)∈d×1×{-1,+1},1≤i≤m}，其中d是样本维数，m是样本个数.样本集X可以划分为2个子集：1)所有正样本构成的子集所有负样本构成的子集-1),1≤j≤m-}，其中m+和m-分别表示正样本和负样本的个数，m++m-=m.对于给定的决策函数f(x)，采用非参数假定的估计，AUC计算为

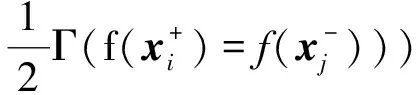
其中，Γ(k)为指示函数(indicator function)，如果k为真，则结果为1，否则结果为0.AUC反映了随机抽取一个正样本的决策值大于随机抽取一个负样本的决策值的概率.AUC优化的目标是在二分类训练样本集上获得决策函数f(x).AUC越大，代表决策函数f(x)的性能越好.由于Γ(k)非凸，也不连续，因而无法直接实现AUC优化.实用的方法一般采用损失替代函数把AUC优化问题转化为凸优化问题.AUC优化等价于最小化经验风险(empirical risk)函数:

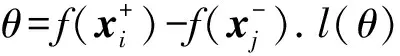
本文针对二分类问题，构建一个线性分类模型.对于线性分类器w，即决策函数f(x)=wTx，AUC计算为

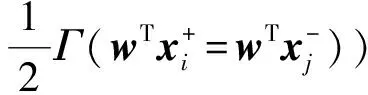
为了避免过拟合，AUC优化通常使用结构风险最小化(structural risk minimization, SRM)策略.本文考虑由L2正则化项和最小二乘损失函数组成的结构风险函数作为目标函数[22-23]，即：

(1)

其中，λ>0是L2正则化参数，用来控制学习模型的复杂度，常数12用于在求导时抵消常数项.式(1)有2个优点：1)最小二乘损失函数对AUC优化具有一致性；2)可以求得解析解.

2 AUC优化的新目标函数

由于传统分类算法的经验风险函数是m个单个样本构成的损失函数之和的均值，为了减少AUC优化问题的规模，本文把式(1)调整为分母为m的形式：

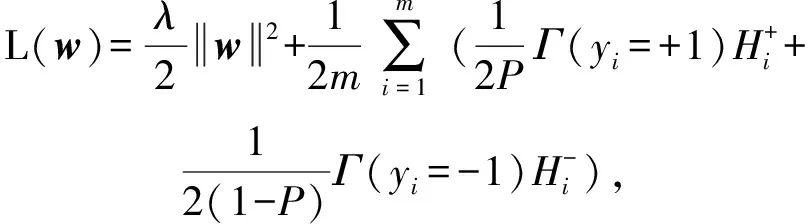
(2)

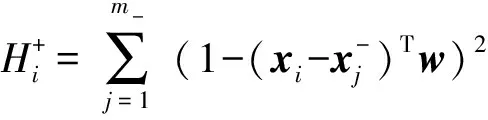
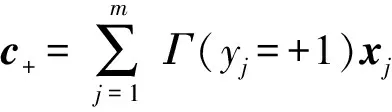
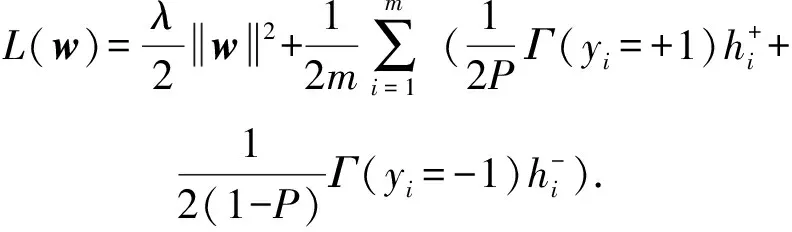
(3)

为了分析式(1)和式(3)之间的关系，本文采用

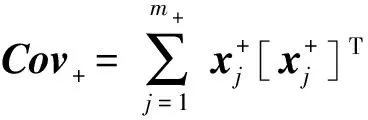
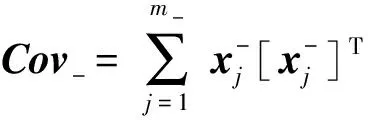
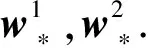
定理1. 当式(3)的正则化参数是式(1)的正则化参数的12时，即最小化式(3)等价于最小化式(1).

证明. 为了区分式(1)和式(3)，记:

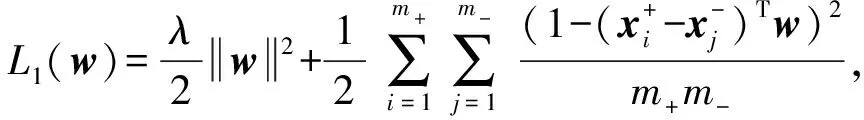
(4)

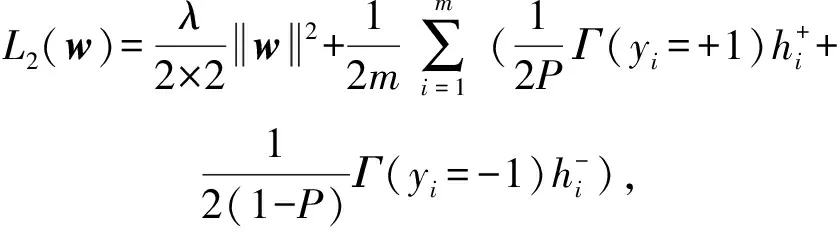
(5)

对式(4)求偏导，其梯度为

由协方差矩阵的性质可知Cov+,Cov-都是半正定矩阵，又因λI为正定矩阵，CCT为半正定矩阵，所以A和A+CCT为正定矩阵，即A和A+CCT可逆.

对式(5)，同样求偏导，其梯度:

其中:

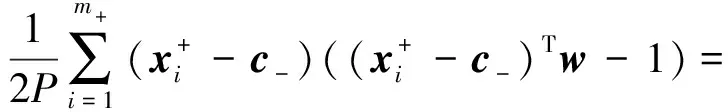
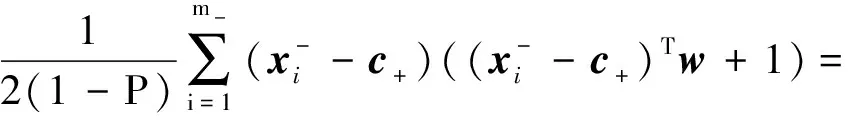
所以:

解析解:

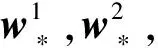
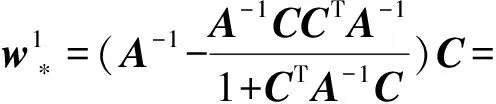
同理:

其中，

α1=1(1+CTA-1C)，
α2=2(1+2CTA-1C).

因为A是正定矩阵，所以A-1也是正定矩阵.由正定矩阵的性质可知，对于任意非0向量C，有CTA-1C>0，因此，α1>0，α2>0.

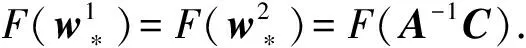
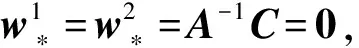
证毕.

3 在线AUC优化的线性方法

由第2节的分析可知，最小化式(3)与最小化式(1)等价，且式(3)与训练样本数线性相关.令:

则式(3)可以转化为

(6)

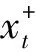
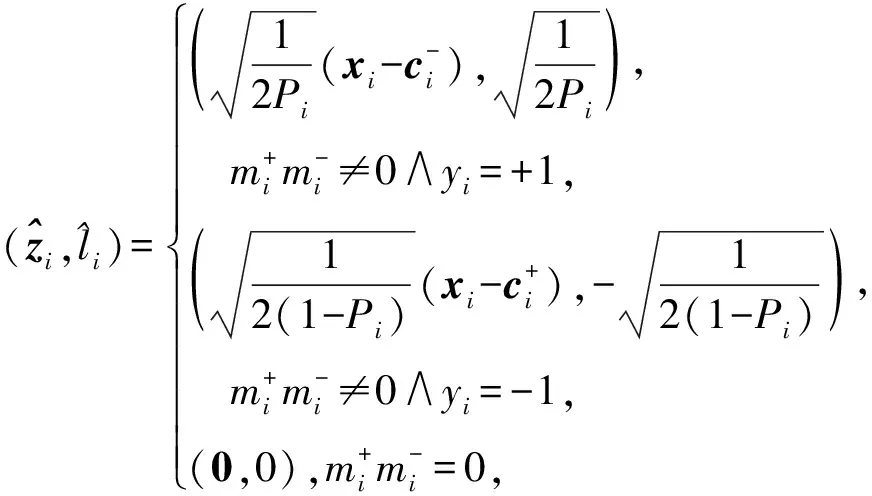
(7)

在上述分析基础上，LOAM算法描述见算法1.

算法1. LOAM算法.

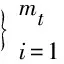
输出：wmt.

② fori=1,2,…,mt

③ 接收新样本(xi,yi);

④ ifyi=+1

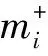
⑥ else

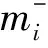
⑧ end if

⑩ 采用ILSC或AdaGrad策略更新分类器wi;

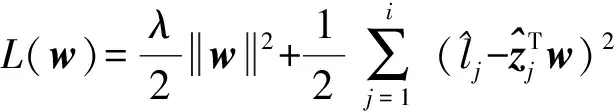
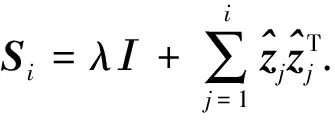
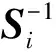
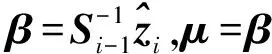
算法2详细描述了ILSC更新策略.

算法2. ILSC更新策略.

输入：正则化参数λ;

输出：wmt.

② fori=1,2,…,mt

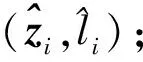
④ ifi=1

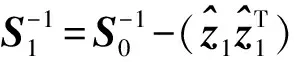
⑥ else

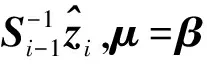
⑧ end if

⑨ end for

第2种分类器更新策略为AdaGrad方法.记gi为第i次迭代时的梯度，gi,j为gi的第j维，η为学习率.与在线梯度下降方法对每个特征设置相同的学习率不同，AdaGrad方法使得出现频率较低的特征具有较高的学习率，出现频率较高的特征具有较低的学习率，每一维的迭代更新规则为

其中，δ>0是平滑参数，用于避免分母为0，通常设置一个非常小的值.算法3详述了AdaGrad更新策略.

算法3. AdaGrad更新策略.

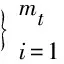
输出：wmt.

① 初始化：w0=g0=0.

② fori=1,2,…,mt

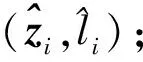
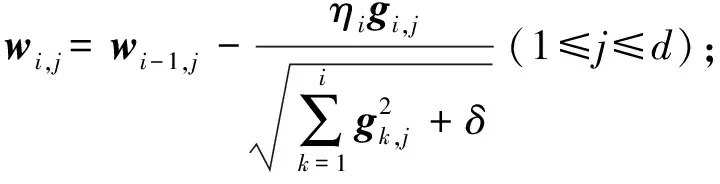
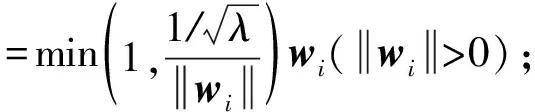
⑦ end for

4 实验分析

本文通过基准数据集和高维稀疏数据集上的大量实验验证新算法的有效性，数据集来自LIBSVM①,UCI②,SVMLin③.由第2节分析知，最小化式(3)等价于最小化式(1)，因此本文对比了新算法LOAM和优化式(1)的多个在线算法.实验对比了5个算法：

1) AdaOAM算法.利用AdaGrad方法对式(1)进行优化求解[23].

2) OPAUC算法.利用随机梯度下降方法对式(1)进行优化求解[22].

3) OPAUCs算法.OPAUC算法的变体，用来处理高维稀疏数据任务[28].

4) LOAMILSC算法.采用增量式最小二乘法更新分类器.

5) LOAMAda算法.采用AdaGrad方法更新分类器.

4.1 基准数据集上的实验结果

16个基准数据集如表1所示包含二类数据集和多类数据集.AUC是衡量二分类算法性能的评价指标，实验中将多类数据集转化为二类数据集，表1中的不平衡率(imbalance ratio)统计出了多样本类与少样本类的样本数之比.

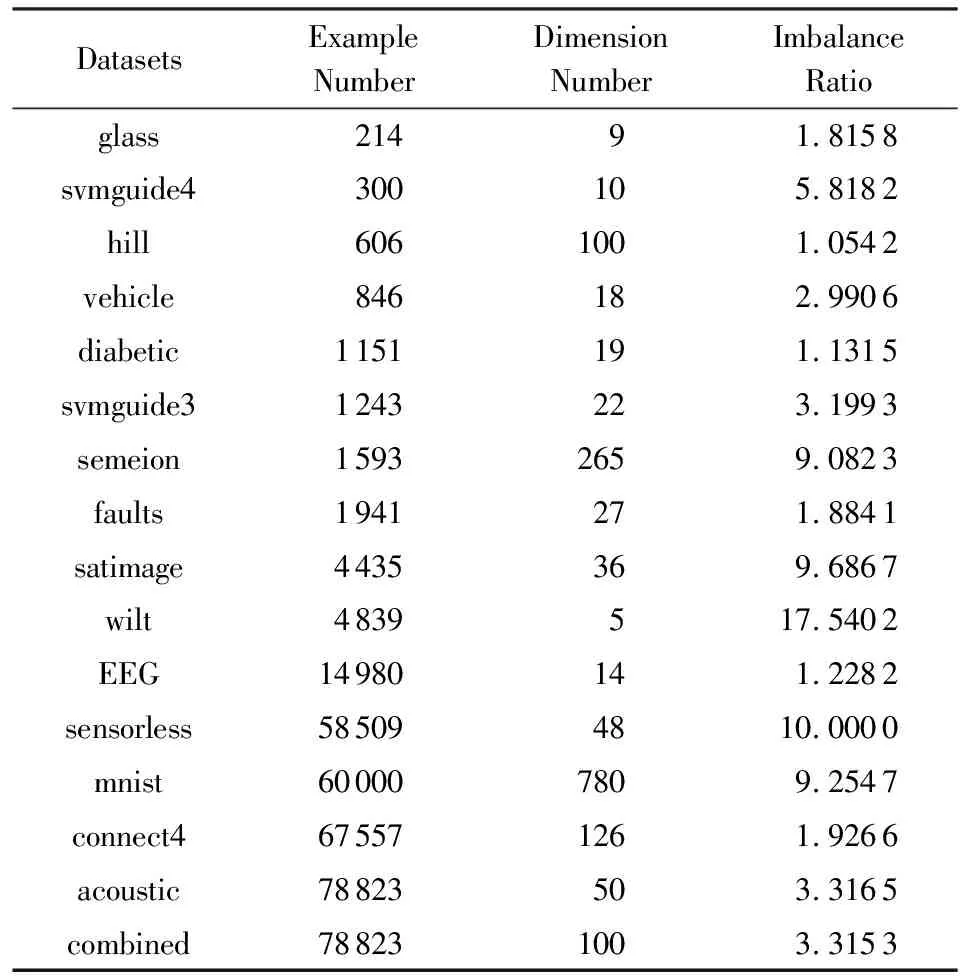
Table 1 The Detailed Information of Benchmark Datasets表1 基准数据集详细信息

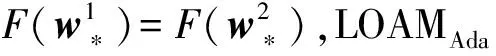
为了减少随机分组对实验结果的影响，对每个数据集使用5次5折交叉验证，总共实验25次，实验结果是测试集上25次AUC的平均值，记录方式为“平均值±标准差”.

表2为4种算法在基准数据集上的AUC结果.由表2知：1)LOAMILSC算法在多数数据集上显著优于LOAMAda,AdaOAM,OPAUC算法.由标准差知，与后者相比，LOAMILSC算法更加稳定.2)LOAMAda算法与AdaOAM和OPAUC算法的性能基本相当.

图1显示了4种算法在基准数据集上的运行时间(单位ms).其中，横轴为各个基准数据集，纵轴为对数坐标(log-scale)，4条柱状图从左至右依次表示LOAMAda,LOAMILSC,AdaOAM,OPAUC算法的运行时间.由图1知：LOAMAda算法的运行效率最高，其次为LOAMILSC算法；AdaOAM和OPAUC算法的运行效率最低，且基本相当.

随着数据集维数的增加，LOAMILSC,AdaOAM,OPAUC算法的运行时间与LOAMAda算法运行时间之间的差距变大.例如在数据集mnist上，LOAMILSC,AdaOAM,OPAUC算法的运行时间是LOAMAda算法的几十倍甚至上百倍.这是由于LOAMILSC算法涉及逆矩阵的存储和计算，AdaOAM和OPAUC算法涉及协方差矩阵的存储和计算；这3个算法的空间复杂度和每次迭代的时间复杂度均为O(d2).对比而言，LOAMAda算法只需要存储平均值，其空间复杂度和每次迭代的时间复杂度仅为O(d).总之，LOAMAda算法的空间复杂度和每次迭代的时间复杂度比LOAMILSC,AdaOAM,OPAUC算法低一个量级.

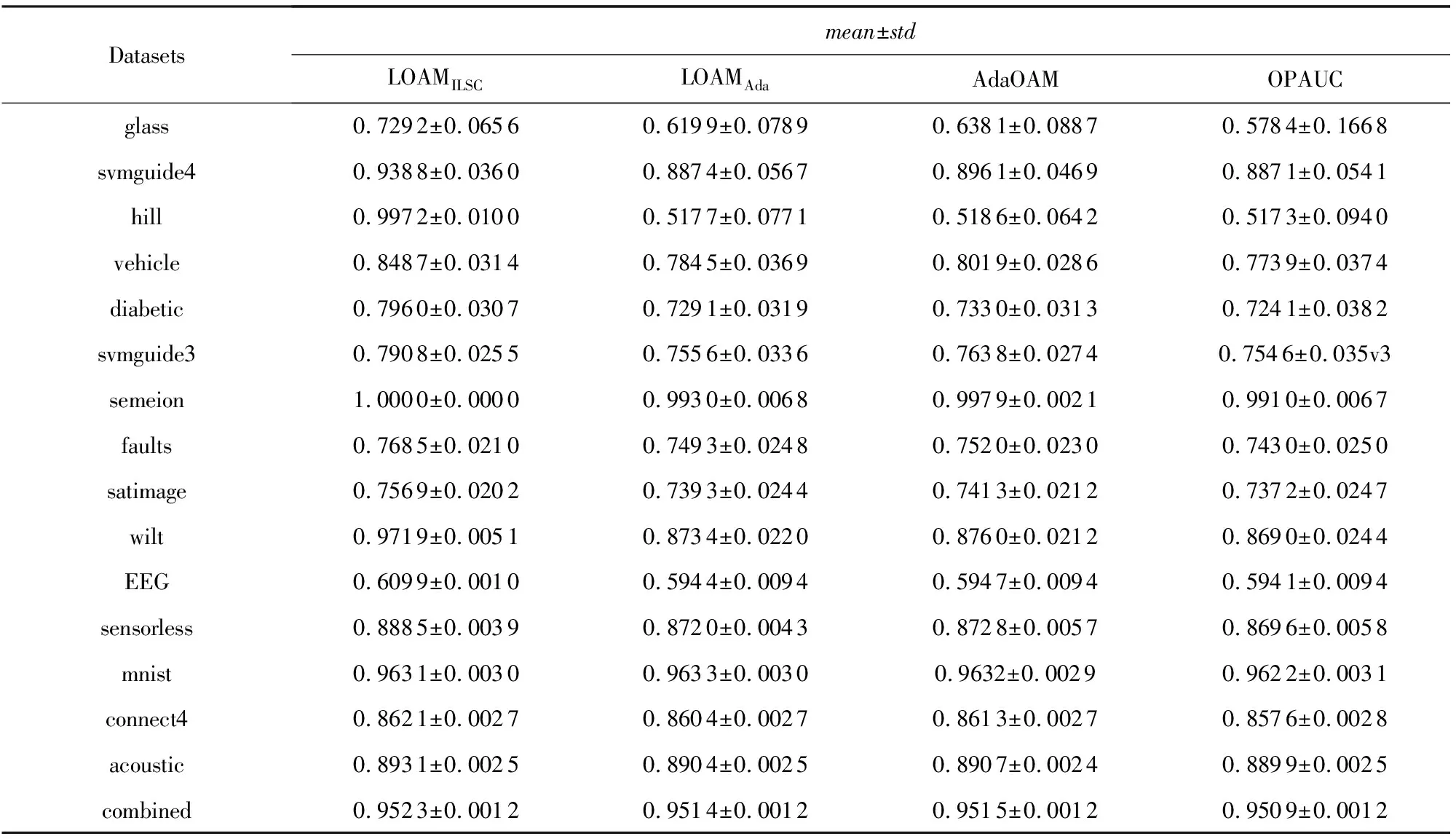
Table 2 The AUC Results of Four Algorithms on Benchmark Datasets表2 4种算法在基准数据集上的AUC结果

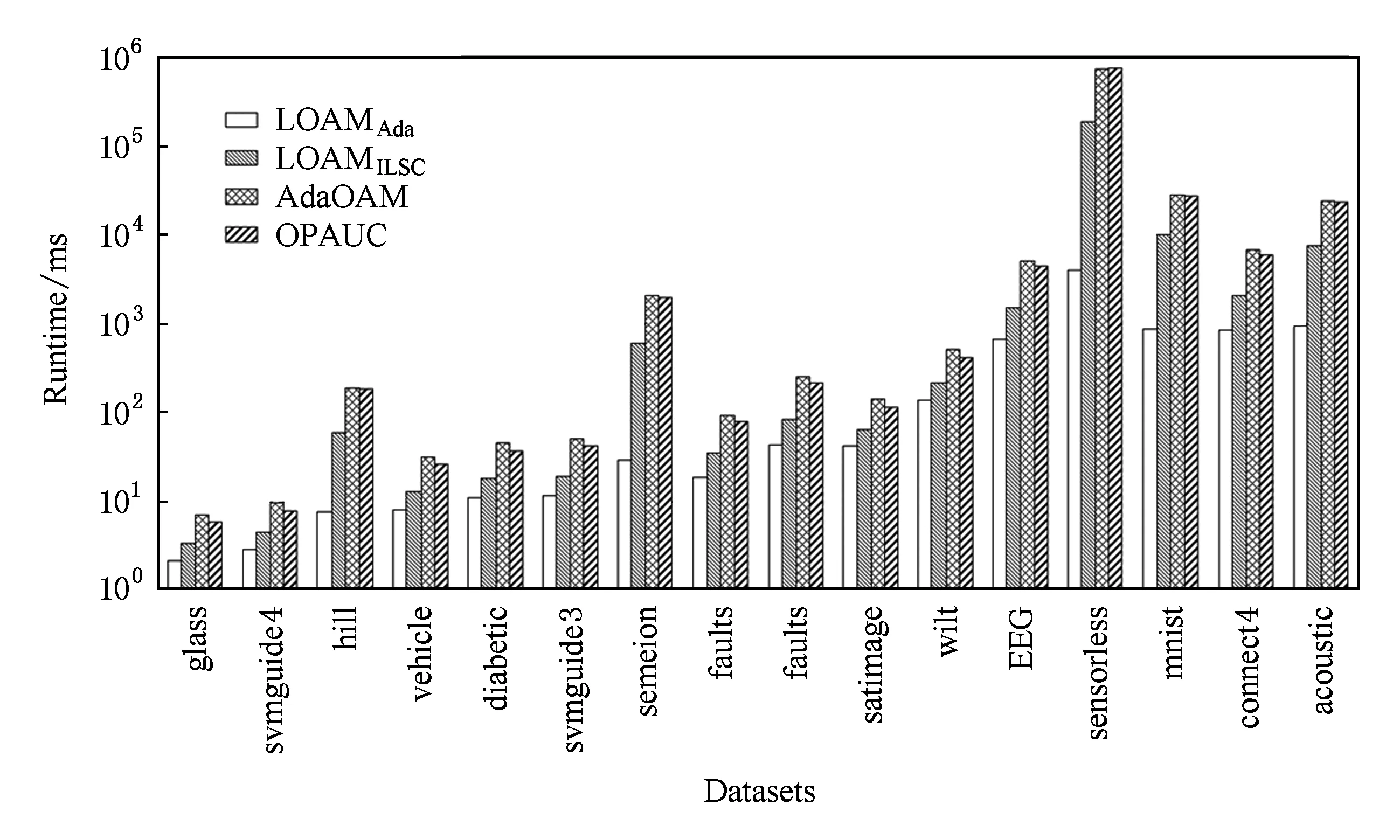
Fig. 1 The runtime of four algorithms on benchmark datasets图1 4种算法在基准数据集上的运行时间

图1和表2所示的实验结果对比表明:LOAMILSC算法的AUC性能最优最稳定；LOAMAda算法的运行效率最高，更适合处理实时或者高维学习任务.

4.2 高维稀疏数据集上的实验结果

本节进一步在6个高维稀疏数据集(如表3所示)上验证了LOAMAda算法在处理高维学习任务时的高效性.对于其中的多类数据集，将其转为二类不平衡数据集.

由于LOAMILSC,AdaOAM,OPAUC算法的空间复杂度和每次迭代的时间复杂度均为O(d2)，而6个高维稀疏数据集的维数均超过20 000维，考虑到时间和存储开销，本节只对比了LOAMAda和OPAUCs算法.

与4.1节相同，本节采用1次5折交叉验证选择最优参数，OPAUCs算法的参数选择范围参照文献[28]，步长参数选择范围为2[-12:10]，正则化参数选择范围为2[-10:2]，参数τ=50.LOAMAda算法的步长参数选择范围为2[-12:10]，正则化参数选择范围为2[-11:1].同样对每个数据集使用5次5折交叉验证，实验结果为测试集上25次AUC的平均值.

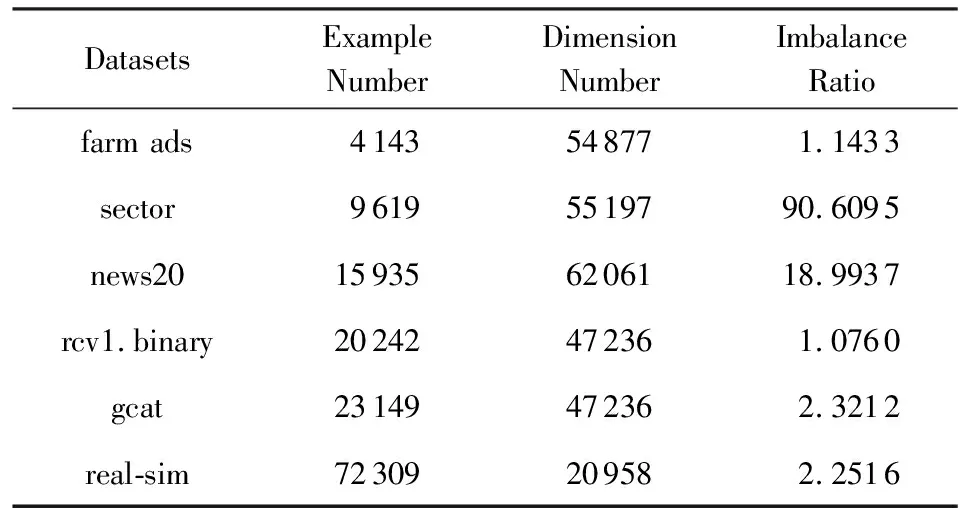
Table 3 The Detailed Information of High DimensionalSparse Datasets

表4为LOAMAda和OPAUCs算法在高维稀疏数据集上的AUC结果.由表4所示，LOAMAda算法的平均值高于OPAUCs算法、标准差小于OPAUCs算法.这表明LOAMAda算法的AUC性能优于OPAUCs算法且更加稳定.

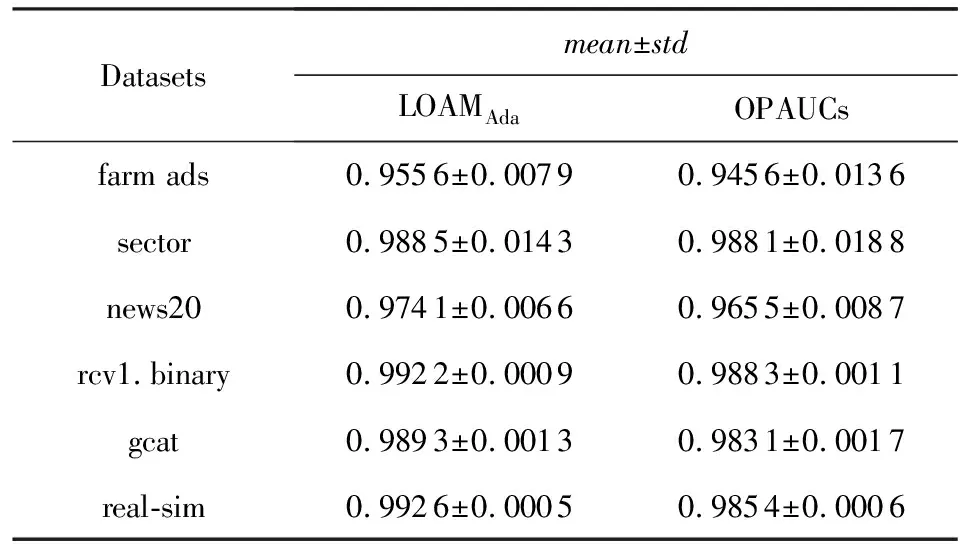
Table 4 The AUC Results of LOAMAda and OPAUCs onHigh Dimensional Sparse Datasets

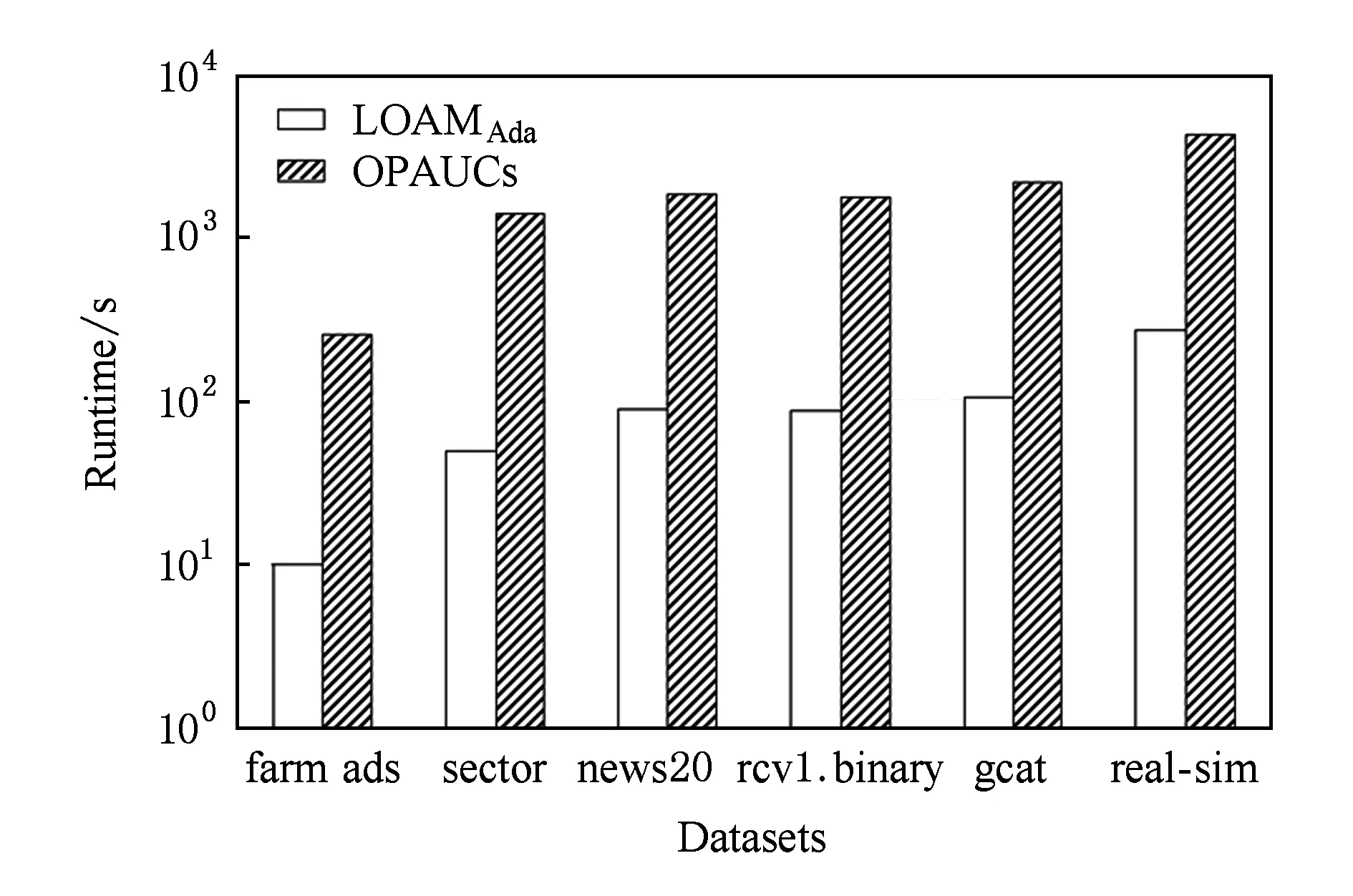
Fig. 2 The runtime of LOAMAda and OPAUCs on high dimensional sparse datasets图2 算法LOAMAda和OPAUCs在高维稀疏数据集上运行时间

图2为LOAMAda和OPAUCs算法在高维稀疏数据集上的运行时间(单位s)，其中横轴为各个高维稀疏数据集，纵轴为对数坐标，2条柱状图从左至右依次表示LOAMAda,OPAUCs算法的运行时间.图2说明：LOAMAda算法的运行时间远低于OPAUCs算法的运行时间.对比结果表明LOAMAda算法更为高效，更适合处理高维数据.

5 总 结

本文提出一种AUC优化的目标函数，最小化该目标函数等价于最小化由L2正则化项和最小二乘损失函数组成的AUC优化的目标函数，但该目标函数仅与训练样本数线性相关.基于该目标函数，提出了在线AUC优化的线性方法LOAM，并分化出2种LOAM算法：采用增量式最小二乘法更新分类器的LOAMILSC算法和采用AdaGrad方法更新分类器的LOAMAda算法.LOAMILSC算法和LOAMAda算法仅需扫描一遍训练集，不需要存储任何旧样本；它们的空间和时间复杂度分别与ILSC和传统在线梯度下降算法相同.实验对比表明，LOAMILSC算法的AUC性能最优也最稳定，而对于实时或高维学习任务，LOAMAda算法则更加高效.