面向异构语义映射的D3L转换算法及其性质研究

赵晓非 史忠植 冯志勇

1(天津工业大学计算机科学与软件学院 天津 300387) 2(中国科学院计算技术研究所智能信息处理重点实验室 北京 100190) 3(天津大学计算机科学与技术学院 天津 300072)

在信息集成、服务集成以及语义Web等大量的分布式应用中，人们常希望本体是分块的或分布式的，而不是单一的本体；大规模本体的模块化具有更强的针对性、更高的推理效率[1].上述2个原因使得分布式、模块化本体[2-3]成为近几年的研究热点之一.多种的逻辑基础被相继提出，如ε-连接框架[4]、保守扩展的分布式本体框架[5]、分布式一阶逻辑[6]以及基于包的描述逻辑等.作为其中的一个重要的研究分支，分布式动态描述逻辑(distributed dynamic description logics, D3L)[7]引入了语义映射的描述机制、本体间知识的传播机制以及面向分布式环境的推理机制.D3L很好地满足了每个局部信息系统希望保持一定程度的自治及自己的用户界面而从其他局部信息系统导入和重用知识的需求，因而为上述应用提供了较完备的逻辑基础.

本体间元素的映射和推理是模块化本体要解决的核心问题.由于现实世界中语义映射的多样性，其逻辑基础必须能够建模异构元素之间的映射并进行推理.不幸的是，现有的研究对此均没有提供足够的支持.以ε-连接框架为例，尽管该框架提供了基于消解的分布式推理算法，但通过ε-连接构造的映射仅限于不同本体的概念之间，因而无法实现异构元素之间的映射和推理.保守扩展的分布式本体框架所提供的推理仅适用于本体之间具有签名依赖性的情形，不符合改约束条件的映射均无法被描述和推理，并且该框架仅从理论上证明了签名依赖性问题是可判定的，并没有提供推理算法.

鉴于此，本文将研究扩展到了被包含端存在复合元素的异构桥规则情况下的D3L推理问题.由于分布式Tbox是D3L知识库最基本的形式，为了获得分布式Tbox的可判定性，首先给出了其正则性的定义.而后针对将动态描述逻辑DSROIQ作为局部本体语言的D3L知识库，通过对桥规则进行必要的形式变换以及区分不同情形转换为已有的语言机制，提出了将分布式知识库转换为单一DSROIQ知识库的算法.接着我们对转换算法的性质进行了研究.证明了算法可以在多项式时间内终止、算法的目标知识库与原始知识库在可满足性上是等价的，进而证明了在上述桥规则存在的情况下正则D3L知识库的集中式推理具有与单一DSROIQ知识库推理相同的最坏时间复杂度.本文的算法使得D3L推理可以获得与现有的分布式推理算法相同的最坏时间复杂度并且解决了后者难以处理异构复合桥规则的问题.

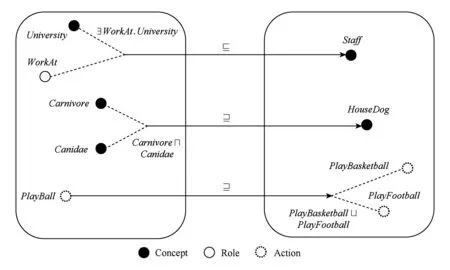
Fig. 1 Sample for heterogeneous composite bridge rules图1 异构复合桥规则示例

1 分布式动态描述逻辑

限于篇幅，在此仅对与本文联系密切的D3L 相关部分进行简要阐述，更详细的信息请参考文献[8].首先介绍动态描述逻辑DSROIQ中的概念、角色和动作，然后介绍DSROIQ之上的分布式知识库及其解释的相关知识.

定义1. DSROIQ的概念是下述情形之一的表达式：

其中,A表示原子概念;C，D表示普通概念;a表示个体;R，S表示角色;n为正整数.

DSROIQ允许角色之间进行2种运算：连接运算和逆运算.R∘S表示角色R和S的连接;而S-表示角色S的逆.DSROIQ的角色包含公理(RIA)是形如S1∘S2∘…∘SnR的表达式.RIA的集合可以构成角色层次.给定局部TboxTB以及个体t，u，从t到u的路径是角色的1个非空序列R1(x1，x2)，R2(x2，x3)，…，Rn(xn，xn+1)∈TB，其中x1=t，xn+1=u且xi≠xi+1，1≤i≤n.如果不存在起始于个体t的路径，则称t为终端;如果不存在终止于个体t的路径，则称t为始端.

定义2. 如果1个角色层次中的角色之间存在满足2个条件的偏序关系：

1)SR当且仅当S-R；

2) 每个RIA是满足SiR，i=1，2，…，n的下列表达式之一：R∘RR，R-R，S1∘S2∘…∘SnR，R∘S1∘S2∘…∘SnR，S1∘S2∘…∘Sn∘RR,则称该角色层次是正则的.

定义3. DSROIQ的原子动作α=(P，E)定义如下：

1)α为原子动作名；

2)P是由公理组成的有限集合，表示动作执行前必须满足的前提条件；

3)E是由公理组成的有限集合，表示执行该动作后将会发生的影响.

D3L知识库[9]的最基本形式——分布式Tbox由局部Tbox的集合和提供局部Tbox之间映射的桥规则的集合构成，每个局部Tbox建立在独立的动态描述逻辑语言之上.DSROIQ之上的分布式Tbox的定义如下：

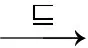
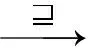
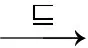
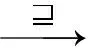
分布式TboxDTB的1个解释I={Ii}i∈I，{ri j}i，j∈I，i≠j，其中{Ii}i∈I是局部解释的集合，{ri j}i，j∈I，i≠j是领域关系的集合.对于每个i∈I，有每个领域关系ri j是的子集且有ri j(d)={d′|d，d′∈ri j}.

定义5. 解释I满足分布式TboxDTB中的元素或公理(记为I·)，当且仅当I满足11种情形(i，j∈I)：

10)DTBi：CD，如果对任意解释I，IDTB成立蕴含Ii：CD成立；

11)DTBi：RS，如果对任意解释I，IDTB成立蕴含Ii：RS成立.

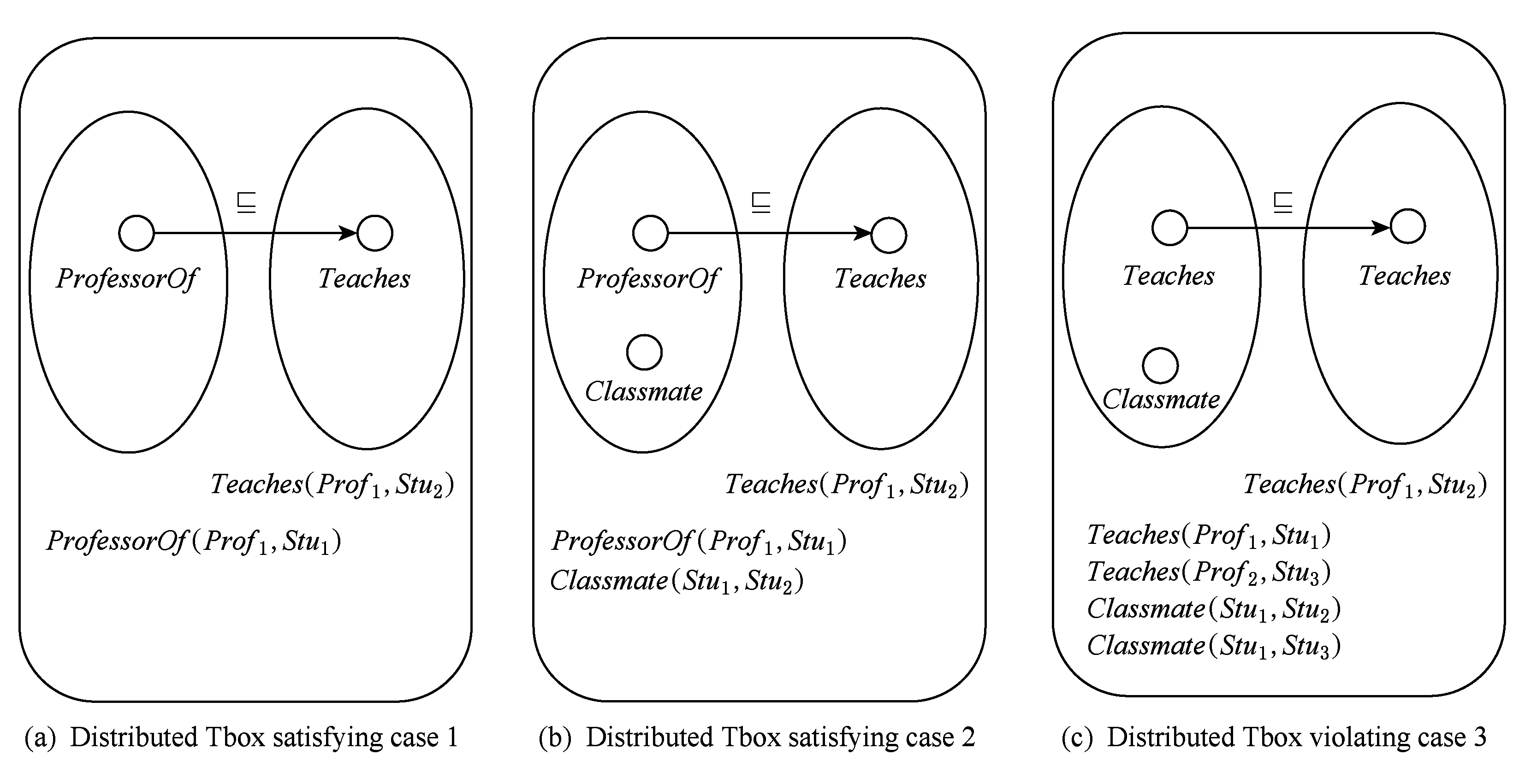
Fig. 2 Sample for the regularity of distributed Tbox图2 分布式Tbox的正则性示例

2 异构复合桥规则的转换方法

2.1 DTB的正则性

Horrocks等人[10]对SROIQ进行了系统的研究，发现SROIQ的正则Tbox——即仅允许存在正则角色层次的Tbox——的基本推理问题是可判定的.引入动作理论之后，Chang等人[11]的研究表明动作理论的引入并不改变原有描述逻辑推理问题的可判定性.为了获得以DSROIQ作为局部本体语言的DTB的可判定性，我们对定义2进行扩展，得到分布式Tbox正则性的定义.

定义6. 如果1个分布式TboxDTB的角色层次中的角色之间存在满足3个条件的偏序关系：

1)SR当且仅当S-R；

2) 每个RIA是满足SiR，i=1，2，…，n的下列表达式之一：R∘RR，R-R，S1∘S2∘…∘SnR，R∘S1∘S2∘…∘SnR，S1∘S2∘…∘Sn∘RR；

①v到y不存在路径；

②SR；

③S=R(即B中存在R(z，v))，但不存在R(z′，v′)满足v′到y之间有路径，且若x=z则B中不存在C(x)，若y=v则B中不存在C(y)，

则称该分布式TboxDTB是正则的.

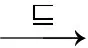
有关正则性更详细的信息请参阅形式语言与自动机的相关知识.

2.2 预备定理

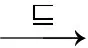
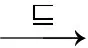
步骤1. 初始化B′=B；

步骤2. 对于B′中每个变元x，令{C1(x)，C2(x)，…，Cn(x)}代表B′中所有引用x的概念公理的集合，迭代计算B′=B′{C1(x)，C2(x)，…，Cn(x)}∪{(C1C2…Cn)(x)}；

步骤1～3在每次迭代过程中对B′中的角色公理的数目进行约简，显然会在有限步骤内结束，而且迭代过程结束后，B′中所有路径的终端个体只能是作为H中角色公理的第2个参数出现的个体，因此所有路径都终止于该终端个体.如果H=C(x)则按照上述步骤，所有路径都已被约简去除，因此B′中不存在任何路径.

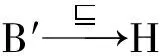
证毕.

以桥规则worksAt(x，y)University(y)supervises(x，z)PhDStudent(z)profOf(x，z)为例，其中B=worksAt(x，y)University(y)supervises(x，z)PhDStudent(z)经过转换，得到的B′=∃worksAt.University(x)supervises(x，z)PhDStudent(z)，其中z为单一的最大路径的终端.

由于桥规则本质上描述的是跨本体的包含关系，因此尽管定理1针对的是into-桥规则的情形，对于onto-桥规则同样有类似的结果，可对被包含端进行同样的转换，其证明思路与定理1类似，此处不再赘述.

2.3 带异构复合桥规则的D3L知识库转换算法

根据定理1可知，复合桥规则的角色路径均可等价转换为单一的线性路径，其中每个个体变元均属于该最大路径的一部分.文中我们假定所处理的桥规则均具有定理1等价变换后的形式.

在定理1的基础上，通过全面考虑构成异构复合桥规则的不同形式，我们研究了异构复合桥规则的转换语义并给出了分布式知识库的转换算法.该算法可以将DSROIQ作为局部本体语言的D3L知识库转换为单一的DSROIQ知识库.

算法1. D3L知识库的转换算法.

输入：以DSROIQ作为局部本体语言的分布式知识库DTB：{Ti}i∈I，BR；

输出：单一的DSROIQ知识库TBBR.

步骤1. 初始化TBBR=∅，初始化剩余桥规则的集合BR′=BR；

步骤2. 若BR′=∅，则令TBBR=TBBR∪{Ti}i∈I，输出TBBR，算法结束；

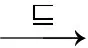
步骤4. 分5种情形判断：

1) 若B中存在引用同1个体变元z的2个概念公理D(z)和D′(z)，则将两者从B中删除并将(DD′)(z)加入B中；

2) 若H=C(x)且B=D(x)，则将该桥规则从BR′中删除并将DC加入TBBR；

3) 若H=R(x，y)且B形如{R1(x，x2)，R2(x2，x3)，…，Rn(xn，y)}，则将该桥规则从BR′中删除并将R1∘R2∘…∘RnR加入TBBR；

4) 若H=R(x，y)且B中存在D(z)满足z出现在B或H的角色公理(第1参数或第2参数均可)中，则执行3步骤：

① 引入新角色S，将D=∃S.Self加入TBBR；

② 引入新变元z′，将角色公理S(z，z′)加入B，将每个角色公理T(x′，z)∈B替换为T(x′，z′)，将每个角色公理T(z，y′)∈B替换为T(z′，y′)；

③ 将D(z)从B中删除，若z=y则将H替换为R(x，z′)；

5) 若H=C(x)或H=R(x，y)且B中存在D(z)满足z既不出现在H中也不出现在B的任意角色公理中，则执行2步骤：

① 引入新变元u，若存在R(x，t)∈B则令u=y，否则令u=x；

② 将B中D(z)替换为∃U.D(u)，其中U为全局角色；

步骤5. 跳转到步骤2.

算法1从剩余桥规则的集合BR′中依次取出桥规则进行处理，直至BR′为空，算法1终止.在处理每条桥规则的过程中，分5种情形处理.其中桥规则经过情形1、情形4和情形5进行转换和约简，直到满足情形2或情形3时被最终从BR′中删除.下面我们分析一下这5种情形是否涵盖了所有可能的情况.我们可以通过桥规则的形式若不满足情形1～4,则必然满足情形5的思路来进行证明.假定情形1～4的前提条件均不满足，由于桥规则的包含端为非复合元素，因此H无外乎2种情况：H=C(x)或H=R(x，y).如果H=C(x)，根据定理1可知B中不存在角色公理，即B中只能是概念公理.由于情形2的前提条件不满足，即B不是D(x)的形式，则必有D(z)∈B存在，且z既不出现在H中也不出现在B的任意角色公理中，情形5的前提得以满足.如果H=R(x，y)，根据定理1可知B中的所有路径均被包含于1个单一的最大路径中且y是该最大路径的终端.由于情形3的前提条件不满足，即B不具备R1(x，o1)，R2(o1，o2)，…，Rn-1(on-2，on-1)，Rn(on-1，y)的形式，因此必有概念公理D(z)∈B存在.再根据假设，情形4的前提条件不满足，也就是z不出现在B和H的角色公理中，因此情形5的前提条件得以满足.通过上述分析可知，无论H=C(x)或H=R(x，y)，如果桥规则的形式不满足情形1～4，则必然满足情形5，因此算法所区分的5种情形涵盖了所有可能的情况.

下面通过实例对算法的执行加以说明.以2.2节中的桥规则为例，详细的中间结果列于表1中.经过算法1的转换，最终可得3条DSROIQ公理(其中S1，S2为新引入的辅助角色)：S1∘supervises∘S2profOf;∃worksAt.University≡∃S1.Self;PhDStudent≡∃S2.Self.

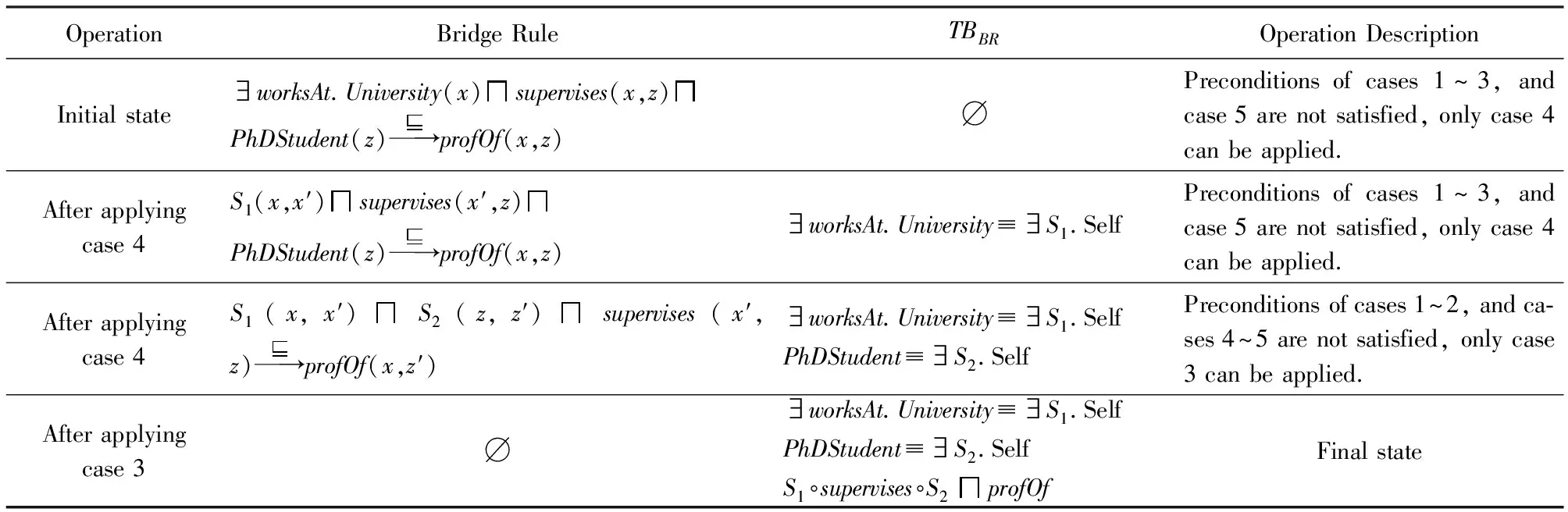
Table 1 Sample for the Transformation of Bridge Rules表1 桥规则转换示例

3 D3L集中式推理的计算复杂度

下面我们对算法1的性质以及复杂桥规则情况下D3L集中式推理的计算复杂度问题进行研究.定理2阐述了算法1的时间复杂度问题.定理3阐述了算法1输出的目标知识库TBBR与原始知识库DTB在可满足性上是等价的.定理4阐述了DTB的正则性与TBBR正则性的关系,进而证明了复合桥规则存在的情况下D3L的集中式推理具有与单一DSROIQ知识库推理相同的最坏时间复杂度.

定理2. 算法1将在多项式时间内终止.

证明. 显然算法1的单个步骤均可在线性时间内完成，因此对算法总体时间复杂度有影响的只有每个步骤执行的次数.下面对每步所执行的次数进行分析.步骤1～3可以在多项式数目步骤内完成，我们主要分析步骤4.情形1和情形4约简了桥规则中概念公理的个数.由于在约简过程中并不引入新的概念公理，因此对于每个概念公理，无论是情形1或情形4至多执行1次.情形2～3约简了桥规则的个数，同样可以在多项式步骤数内结束.情形5约简了概念公理的个数，这些公理不存在出现在桥规则的包含端中的个体变元.由于在情形5的执行过程中并不引入此种概念公理因此可以在多项式步骤数内结束.

综上所述，算法1将在多项式时间内终止.

证毕.

定理3. 算法1输出的知识库TBBR与DTB具有相同的可满足性.

证明. 要证明TBBR与DTB具有相同的可满足性，可以归纳地证明算法的每步转换都不改变可满足性即可.令TB0BR0和TB1BR1分别代表1个转换步骤执行之前和之后的TBBRBR′，我们需要证明TB∪TB0∪BR0和TB∪TB1∪BR1具有相同的可满足性.

情形1～3均为等价替换，不会改变转换前后的知识库可满足性.

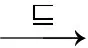
反过来，若TB∪TB1∪BR1是可满足的(即存在解释ITB∪TB1∪BR1)，我们来证明TB∪TB1∪BR0也是可满足的.根据假设可知对于任意变元赋值π均有(B1H1)I，π为真.与前面类似，我们只需考虑为真的情况即可.令π′表示π′(z′)=π(z)，π′(x)=π(x)(当x≠z′时)的变元赋值，很显然为真，考虑到假设条件(B1H1)I，π′为真可知为真，因此有为真.对于在H0中出现的所有变元，π′与π均相同，因此为真，进而IB0H0.最终可得ITB∪TB1∪BR0成立，即TB∪TB1∪BR0是可满足的.

综上，情形4不改变转换前后的知识库可满足性.

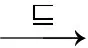
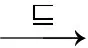
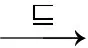
通过上述分析可知，算法1的每步转换均不改变知识库的可满足性，因此TBBR与DTB具有相同的可满足性.

证毕.

定理4. 若DTB是正则的，则算法1输出的知识库TBBR也是正则的.

证明. 我们只需证明算法1的每步转换都不改变知识库的正则性即可.

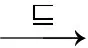
对于情形4，若新引入的角色S先序于H中的角色R(x，y)且S为B中的单一最大路径带来新的始端元素替换了先前作为路径起始的R(s，t)中的始端s，或者S为B中的单一最大路径带来新的终端元素替换了先前作为路径终点的R(s，t)中的终端t，只有这2种情况下知识库的正则性才有可能被改变，然而根据情形4的前提条件可知，在上述情况下被约简的概念公理D(z)只能是D(x)或D(y)两者之一，因此S的引入都不会改变正则性.

情形5与情形4类似，仅当R中的第1个个体变元构成B的单一最大路径的始端或第2个个体变元构成单一最大路径的终端时，∃U.D(u)的引入才有可能改变知识库的正则性.在第1种情况下，我们令u=y(参见情形5的步骤①)，此时u并没有替换先前的最大路径的始端，因此正则性并没有被改变；在第2种情况下，我们令u=x，此时u并没有替换先前的最大路径的终端，正则性仍然得以保持.

证毕.

如2.1节所述，检测正则DSROIQ知识库的可满足性问题是可判定的，因此根据定理4可知，若DTB是正则的，则TBBR也是正则的，即检测TBBR的可满足性问题是可判定的.再考虑定理3TBBR与DTB具有相同的可满足性可知检测DTB的可满足性问题是可判定的.考虑到桥规则集合可以在多项式时间内转换为DSROIQ公理(定理2)，可得该问题的最坏时间复杂度与检测TBBR的可满足性问题的最坏时间复杂度相同.最终我们可以得到定理5.

定理5. 给定DSROIQ作为局部本体语言的分布式TboxDTB，必存在单一的DSROIQ TboxTBBR满足TBBR可以在BR规模的多项式时间内被计算出来且TBBR与DTB具有相同的可满足性.若DTB是正则的，则检测DTB的可满足性问题是可判定的，且其最坏时间复杂度与检测TBBR的相同.

4 相关研究

针对复杂的分布式本体系统逻辑基础的研究，国内外研究人员提出了不同的思路和方法，包括基于ε-连接的描述逻辑、分布式动态描述逻辑、基于保守扩展的分布式本体框架、分布式一阶逻辑等.下面对这些研究进行对比分析.

Grau等人[4]和Mossakowski等人[12]提出了一种分布式本体框架，该框架使用ε-连接对各个本体进行组合.利用连接来描述本体间的外化关系，随后将连接应用于存在性限定和值限定可以构造跨越本体的复杂概念(例如利用连接E∈εi j和Tj中的概念C可以构造Ti中的概念∃E.C，其中εi j是Ti和Tj之间有向连接的集合).文献[13]对该框架进行了模态化扩展并引入了一系列消解推理规则，为其提出了基于消解的分布式推理算法.ε-连接框架仅对复杂概念之间的语义映射提供了一定的支持，并且其前提条件要求局部领域必须是互不相交的，而此特点就决定了它并不适合于作为语义Web这样的局部异构而又部分交叠的系统的逻辑基础.此外，为了满足局部领域的互不相交性还需要对该框架的表达能力进行多种限制，比如1个本体中的元素不能声明为其他本体中元素的子元素超元素，因而该框架无法实现包含关系在不同本体之间的传播.尽管在局部本体组合和推理方面该框架解决得较好，与D3L相比，ε-连接框架的描述能力和知识传播能力较有限.

文献[14]对D3L中桥规则的属性及其导致的知识传播进行了研究.通过在D3L解释中的领域关系之上引入组合一致性语义解决了包含关系无法在局部本体间正确传播的问题.证明了该语义不改变D3L的原始属性.为扩展后的D3L提出了分布式Tableaux推理算法并证明了该算法是可终止的、可靠的和完备的.文献[7]引入了合取映射桥规则，解决了桥规则包含合取元素时包含关系无法正确传播的问题，在此基础上提出了合取映射桥规则到普通桥规则的转换方法并证明了方法的正确性，从而可将带上述桥规则的D3L的推理问题转化为传统的推理问题.然而上述研究仅针对包含原子元素的同构桥规则，对于包含复合元素的异构桥规则的更一般情形则并没有涉及到，而且所提出的分布式Tableaux推理算法是采用局部本体推理加消息传递的机制实现的，其时间复杂度与单一本体的推理相比并没有明显的优势.

Lutz等人[5]提出的分布式本体框架使用保守扩展来描述本体之间的联系.本体T1∪T2是本体T1关于签名Σ的1个保守扩展当且仅当T1∪T2关于Σ的每个逻辑结论也是T1的逻辑结论.他们针对多种主流描述逻辑(ALC，ALCQI，ALCQIO，EL)研究了判定该问题以及2个本体之间的签名依赖性问题的可判定性及其推理复杂度.文献[15-16]进一步为该框架引入了模型论语义并研究了相关的推理问题.基于保守扩展的框架不仅可用于分布式本体的集成，也可用于将单个本体分解为不同的模块.然而与D3L相比，该框架的适用性局限于分布式本体之间具有签名依赖性的情形，不符合该约束条件的复合元素之间的映射均不被支持.我们认为过于严格的限制条件降低了该框架对分布式特性的描述和推理能力，并且该框架仅从理论上证明了签名依赖性问题是可判定的，并没有提供本体推理算法.

此外，基于对传统分布式一阶逻辑(DFOL)的语义映射机制进行扩展，Chiara等人[6]提出了修订版的分布式一阶逻辑.尽管具有较强的描述能力并证明了定理证明方法是完备的和可靠的，然而该框架仅提供的是自然演绎推理的定理证明方式，因此距实际问题中的高效应用尚有一定距离.

5 结论及未来工作

本文研究了被包含端存在复合元素的异构桥规则情况下的D3L推理问题.通过扩展角色层次正则性的定义，我们定义了DTB的正则性，提出了将描述逻辑DSROIQ作为局部本体语言的D3L知识库转换为单一DSROIQ知识库的算法,接着研究了算法的性质以及基于该转换的D3L集中式推理的复杂度的相关问题.本文的研究能够有效处理异构复合桥规则，并且表明支持此种桥规则的D3L集中式推理可以获得与现有D3L分布式推理算法相同的最坏时间复杂度.

未来的工作包括将该研究推广到EL，EL++作为局部本体语言的D3L，研究桥规则转换的可能性及方法、分析其复杂度并开发相应的推理机等.