半潜式航行体水平定深回转运动研究

吴小兵，欧阳凌浩

(1.海军研究院，北京 100161；2.中国船舶重工集团公司第七一〇研究所，湖北 宜昌 443003)

0 引言

反水雷是最早应用无人系统的军事领域，随着技术的发展，不断有各种新型无人系统投入使用，从最初的采用ROV技术的灭雷具，到目前各类UUV、USV形态的无人猎、扫雷系统。不同形态的无人反水雷系统有其特有的应用场合，能为海上编队提供实时水雷防御能力的无人遥控猎雷系统就是其中特殊的一类。该类装备兼顾了高海况适应能力、远距离续航能力、大深度探测能力、实时信息回传能力等特点，采用柴油动力的半潜式航行体拖曳变深声呐执行水雷探测任务，探测信息则通过无线方式实时回传。国外典型装备如美国的AN/WLD-1遥控猎雷系统[1]、法国DCN公司开发的“海上卫士”FDS3遥控猎雷系统[2](如图1-2)。

在作业过程中，半潜式航行体良好的回转机动性可以确保系统的探测精度和作业安全，本文以国外典型半潜式航行体作为原型设计了仿真模型，分析其水平定深回转运动，确定控制方案。

1 航行体六自由度运动方程组

1.1 坐标系

半潜式航行体一般采用回转体结构，可参考鱼雷动力学和运动学模型，建立半潜式航行体空间运动方程组。体坐标系oxyz的原点位于航行体浮心所在横截面与航行体轴线的交点，x轴沿航行体轴线，指向航行体头部；y轴位于航行体纵对称面内，垂直x轴，指向上方；z轴垂直oxy平面，按右手法则指向侧向。地面坐标系ox0y0z0的原点取初始时刻航行体体坐标系的原点在水平面上的投影点，ox0轴沿航行体的纵对称面与水平面的交线，指向前方，oy0轴铅垂向上，oz0轴按右手规则[3]。

体坐标系用于建立航行体动力学方程，地面坐标系主要用于确定几何参数，地面坐标系和体坐标系之间的夹角确定了航行体的3个姿态角：俯仰角θ、偏航角ψ及横滚角φ，体坐标系原点在地面坐标系中的3个坐标x0、y0、z0确定了航行体的空间位置。

地面坐标系到体坐标系的转换矩阵为

体坐标系到地面坐标系的转换矩阵为上述矩阵的转置矩阵，即

1.2 空间运动方程组[4-6]

根据文献[4-6]，利用动量和动量矩定理可以在体坐标系中建立如下的航行体空间运动动力学方程组：

式中：m为航行体质量；vx、vy、vz为速度分量；ωx、ωy、ωz为角速度分量；xc、yc、zc为航行体质心在体坐标系中位置；xb、yb、zb为航行体浮心在体坐标系中位置；G为航行体重力；B为浮力；T为推力；Jxx、Jyy、Jzz为转动惯量分量；X、Y、Z为流体动力主矢量在体坐标系中的3个分量，即阻力、升力、侧力；Mx、My、Mz为流体动力主力矩在体坐标系中的3个分量，即横滚力矩、偏航力矩、俯仰力矩。

航行体的空间位置由下式确定：

攻角α、侧滑角β及速度v的定义式：

α=-arctg(vy/vx)

上述各式构成了航行体空间运动方程组，共含有vx、vy、vz、ωx、ωy、ωz、θ、ψ、φ、x0、y0、z0、α、β、v15个未知量。

2 水平定深回转运动仿真

2.1 仿真工况及初始条件

参照国外典型半潜式航行体设计如下仿真模型：航行体长6.5 m，采用回转体结构，主体直径1.0 m，质量5 000 kg。半潜式航行器使用柴油机作为动力，需采用桅杆结构进行进排气。考虑桅杆高度，航行体的航行深度不大于4 m，初始深度2 m。现设定定深回转深度为2.5 m，取航行速度8～16 kn，每4 kn一个计算状态。垂直舵角3°～12°，每3°一个计算状态，共12个仿真工况。初始姿态角、流体动力角均为零，前水平舵角为平衡舵角。

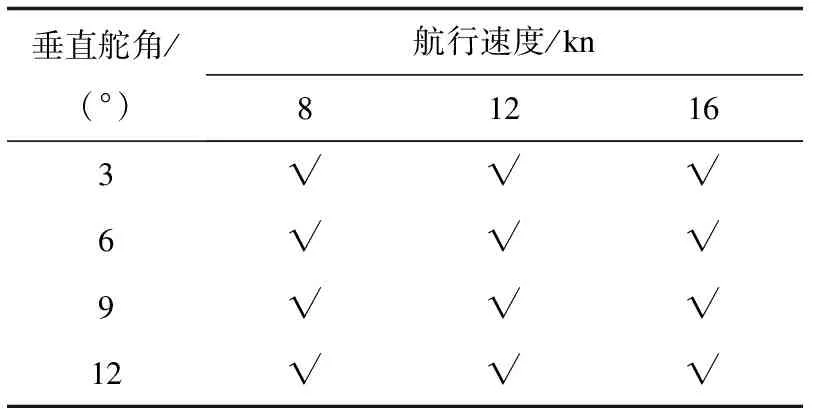
表1 水平定深回转运动仿真工况

2.2 控制方法[7-8]

舵功能分配：前水平舵用于平衡，后水平舵用于定深与横滚控制，后垂直舵为固定舵角。控制方程如下：

定深：δhh=Kyy+Kθθ+Kωzωz

横滚：δd=Kφφ+Kφxφx

2.3 仿真结果

图3-8分别给出了航行体航速8 kn和16 kn及舵角3°～12°下航行体水平面航迹、深度及姿态角变化曲线。

由仿真结果可知：

1)其回转半径随着垂直舵角的增大而减小，最小回转半径为26 m，最大回转半径为103 m。

2)相同垂直舵角条件下，回转半径对航速不敏感，随着航速的增大略有增大。

3)航行体定常回转运动过程中，航行深度与航速、垂直舵角成正比关系，随二者增大而增大。

4)横滚角随航速的增大变化不明显，随垂直舵角的增大而增大。

3 结束语

本文在不同航速和不同垂直舵角下对半潜式航行体的水平定深回转运动进行仿真分析，结果表明：半潜式航行体具有良好的回转机动性能。注意到航速对航行体深度的影响，以及垂直舵角对回转半径、航行深度及横滚角的影响，在实际系统的应用中，应综合考虑航行体回转半径及其姿态进行回转控制。