基于小型三维阵列的瞬态声源快速被动定位方法

黄时春，张焕强，蒋伟康

(上海交通大学 振动、冲击、噪声研究所 机械系统与振动国家重点实验室，上海 200240)

0 引言

近岸监视一直是水声学重要研究领域之一。重物落入水中可能导致港口、航道阻滞，威胁着该水域的安全。沉底重物具有较高的隐蔽性，一旦完成布放就难以发现，因此运用重物在布放落水或沉底过程中产生瞬态声信号进行目标定位，及时发现并妥善处置大型水下投掷物，确保航道和应急通道的畅通，对于国土安全有着至关重要的作用。

近岸海底定位系统一般具有相对静止、隐蔽、耗能低、满足实时定位等特点[1]。因此，单基阵尺度尽量小，在保证精度的前提下算法满足实时定位要求。目前水声被动定位技术主要包括：传统被动定位方法[2]，目标运动分析(Target Motion Analysis, TMA)[3]、匹配场处理(Match Field Processing, MFP)[4]。传统被动定位方法，如三子阵法，已经广泛运用于工程实践中，该类方法具有阵列形式多样，计算量小等特点，但基于纯几何关系得到的精确解往往存在虚根和鲁棒性差的问题[5]；目标运动分析对于声传播特性复杂的浅海，平面波波束形成的性能将严重下降，且计算量较大；匹配场处理充分考虑了声源、信道和环境等一切可利用的信息，但拷贝声场与实际声场的匹配程度决定了算法的定位精度，且该方法计算量大，难以满足实时定位要求。

本文针对传统基于空间几何关系直接计算方法存在虚根和鲁棒性差的问题，提出一种基于最小二乘空间搜索的快速被动定位算法。分析了阵列的设计原则和传声器个数，对比了不同定位方法的计算效率，最后在广场进行了瞬态声源定位实验，验证了三维传声器阵列定位的有效性。

1 瞬态声源特性

重物落水和着底过程中产生瞬态声信号[6]，主要包括：击水声、气泡脉动声和着底声[6]，其中击水声和气泡脉动声统称为落水声。图1和图3表示钢质圆柱体2种姿态落水实测声信号时厉，图2和图4分别表示对应的时频谱图，各个信号短时信噪比如图1和图3所示，短时信噪比定义公式为

(1)

式中：x(n)表示包含噪声的信号；v(n)表示背景噪声信号；N表示所选取的信号长度。当圆柱体横向姿态(轴线与水平面平行)入水时，出现了明显的3种声信号，击水声信号峰值大持续时间短，以宽频为主，气泡脉动声峰值较小，持续时间长，以低频(10～30 Hz)信号为主，着底声持续时间短，以宽频为主。当圆柱体以垂直姿态(轴线与水平面垂直)入水时，未出现明显的气泡脉动声，出现了明显的着底声，具有持续时间短，属于瞬时宽频信号。

2 被动定位原理

在声呐系统、导航等领域广泛运用基于时延估计(Time Delay Estimation，TDE)的声源定位方法[7]，该方法主要分为2步：第1步是求解得到每两个传声器之间的时延；第2步是在获得传声器之间时延的基础上，通过空间几何关系或空间搜索的方式获得声源的空间坐标信息。

2.1 基于广义互相关的时延估计

时延估计常用的有窄带信号时延估计方法和宽带信号实验估计方法，窄带信号时延估计方法一般是通过相位差计算时延，如互谱法等；宽带信号时延估计方法有广义互相法[6]。由于重物落水和沉底信号以宽带信号为主，因此本文运用基于广义互相关的试验估计算法。

假设噪声与声源信号不相关，且传声器接收到的噪声之间不相关，则广义互相关函数可以用下式表示[8]

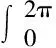
(2)

(3)

文献[9]表明，对于浅水声场中存在多途效应或在弱信噪比情形下采用相位变换加权函数所获得的广义互相关函数精度较好，具有很好的抗干扰能力。主要原因是相位法对功率谱函数进行了白化处理，仅保留信号的相位信息，使得广义互相关函数的峰值更加尖锐，具有抑制噪声和混响的能力。因此本文选用相位变化加权函数进行广义互相关计算。

2.2 基于最小二乘快速搜索的被动定位原理

假设自由空间中存在一个点声源S(x,y,z)，以球面波的形式传播。假设阵列由N个传声器组成，由于位置不同，传声器接收到的信号之间存在时间差，运用上节的广义互相关求出两两传声器之间的时间差。任意取一个传声器作为参考点(如1号传声器)，则声源与传声器之间存在以下空间几何关系。

(4)

式中:(xi,yi,zi)(i=2,…N)表示第i号传感器的空间三维坐标，Δt1i表示第号传声器与参考传声器(1号传声器)之间的到时差，c表示介质中的声速。理论上式(4)中只包含3个未知数，可运用4个传声器建立3个方程进行求解，即N=4。联立方程可得声源坐标的隐式解。

x=p1+q1R

(5)

y=p2+q2R

(6)

z=p3+q3R

(7)

式中

ai=2(x1-xi+1),bi=2(y1-yi+1),ci=2(z1-zi+1),ei=2cΔt1(i+1)

进一步求解式(5)可得到声源坐标的精确解，一般存在两个解，可以根据声源到达传感器的距离远近和测量得到的声程差是否一致来判定声源位置的真伪[5]，但是这种判断有时候也会出错。由于实际工程中，方程中的已知量存在一定误差，如噪声干扰导致的时延估计误差，导致直接求解得到的闭式解鲁棒性差。

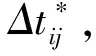
(8)

当目标函数最小时，所对应的(x,y,z)*即为实际声源位置。以上求解过程实质是基于最小二乘最优的空间搜索算法。该计算过程避免了闭式解中存在2个根的问题，通过最小误差的平方和寻求数据的最佳函数，提高了定位算法的鲁棒性。传统的基于空间搜索的定位算法普遍存在计算量大的问题，难以满足实时定位的要求，本文同样运用了搜索的过程，但上述给定不同的R值进行搜索本质属于一维搜索问题。为了进一步提高计算效率，首先运用较大的搜索步长进行搜索，得到初略的估计结果，然后在此基础上缩小搜索范围，减小搜索步长，进行精细化搜索，最终得到精确的定位结果。

3 数值仿真

声基阵可分为直线阵[7]、平面阵[10]和立体阵[11]。理论上由4个传声器组成的空间阵列可实现声源的定位，通过增加传声器数量可提高算法的定位精度，但同样增加了系统的复杂度，以至于定位算法无法满足实时性的要求。因此，在保证定位精度的前提下，选择最合适的基阵类型与传声器数量。

如图5所示，本文采用正四面体的空间立体阵，4传感器分别布置于正四面体的顶点，四面体边长a=0.59 m。适当添加1～2个传声器，其中5号传声器位于四面体几何中心，6号传声器位于原点与1号传声器之间的中点。球坐标系中，在半径R∈(2 m,10 m)，仰角θ∈(-30°，30°),周向角ψ∈(-30°，30°)的空间范围内，随机产生50个瞬态声源，传声器接收到瞬态声信号，采样频率为102 400 Hz，按式(1)所定义的信噪比方式，信号中加入20 dB高斯白噪声，采样时间为0.2 s。瞬态声源信号模型为

(9)

为了对比直接计算法[5]和本文提出的基于最小二乘搜索算法的计算精度和鲁棒性，运用四传声器阵列进行仿真计算，结果如图6和图7所示，其中角度用绝对误差度量，距离误差用相对误差定义。由结果可知运用最小二乘搜索算法的定位精度优于直接计算法。随着距离的增加，两种方法测距误差都有所增大，但最小二乘搜索算法相对更加稳定，即鲁棒性更好。

为了确定合适的传声器数量，本文分别计算了4～6个传声器阵列的定位精度，如图7-9所示。由计算结果可知增加传声器数量可提高声源定位精度。运用4个传声器时，计算误差较大，当增加一个传声器时，定位精度明显提高，仰角误差小于2°。虽然当传声器数量等于6时，定位精度有所提高，但精度提高不明显。因此综合考虑算法定位精度和系统复杂度，本文选择5传声器正四面体基阵。

为了验证本文提出的最小二乘空间搜索定位算法是否满足实时性，分别对比了4种定位算法重复50次定位计算的计算时间。4种方法分别为：直接定位法，基于最大似然搜索(ML)的定位算法、基于快速ML的定位算法和本文提出的最小二乘空间搜索定位算法等4种算法在相同。搜索算法步长一致，分别执行50次定位计算，所消耗的时间如表1所示。由计算结果可知由于直接计算法无迭代的过程，计算效率最高；最大似然搜索算法是全局搜索算法，计算量巨大，因此效率最低，虽然可以通过加速算法大大提高该算法的计算速度，但本文所提出的基于最小二乘搜索的定位算法在计算效率上更具优势，主要原因是该方法本质是一维搜索，且同样运用了由粗到精的层次化搜索。综上所述，本文提出的定位算法同时兼顾了计算精度和计算效率。

表1 4种算法执行50次定位所消耗的计算时间

4 瞬态声源定位试验

为了验证本文提出的定位算法的有效性，广场瞬态声源定位试验。使用羊角锤敲击地面产生瞬态声源，运用五元基阵接收瞬态声波，阵列尺寸详见图3，系统采样频率为102 400 Hz，试验工况设置如图10所示。

分别运用四传声器阵列和五传声器阵列进行声源定位，结果如表2所示。结果表明运用5传感器提高了定位精度和算法鲁棒性，且五元基阵的整体定位精度良好，方向角(仰角和周向角)最大误差不超过3°，随着距离的增加，半径的定位精度下降，如第6组工况中的半径误差等于1 m，这与仿真中的规律相同。

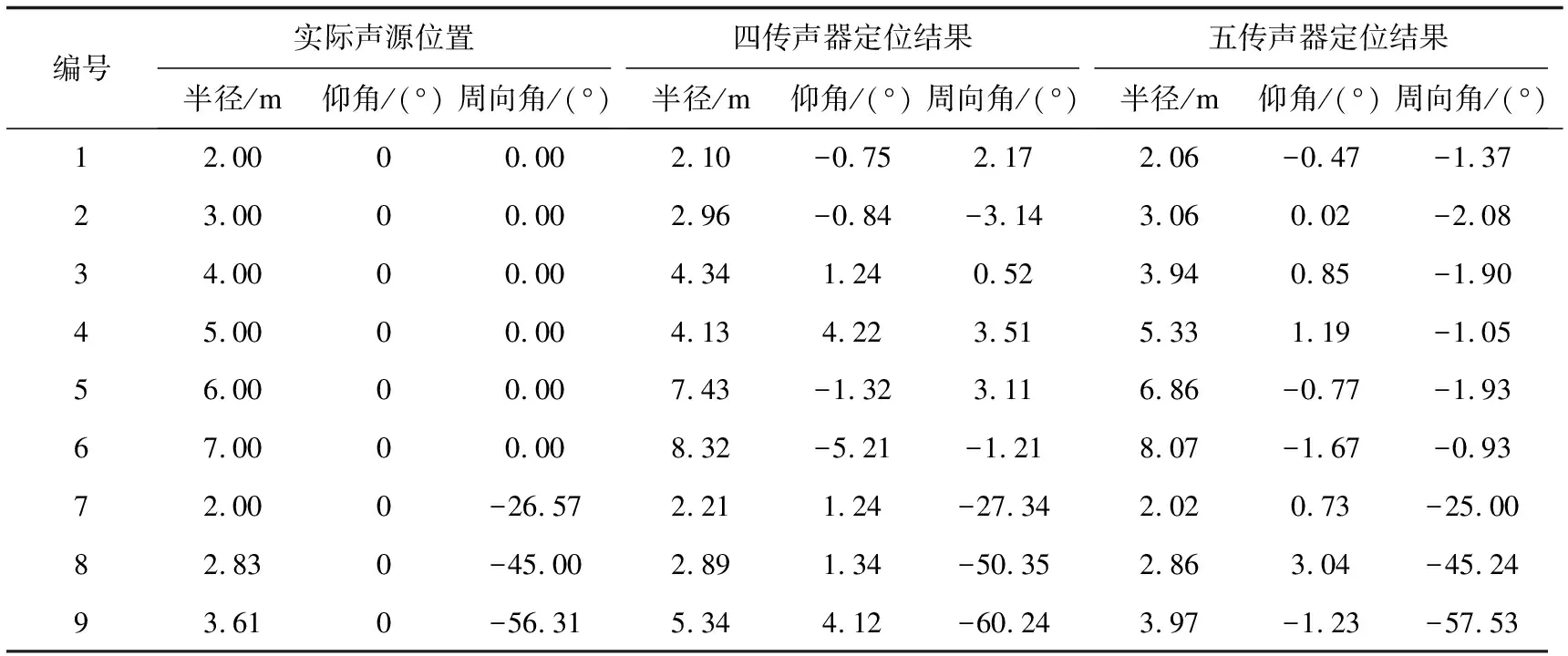
表2 瞬态声定位结果

5 结束语

本文提出了一种基于小型三维阵列的瞬态声源定位方法。该方法根据重物落水声的时频特性，选择合适的广义互相关加权函数计算出传声器之间的声程差，通过运用最小二乘空间搜索算法进行声源定位。将传统三维空间搜索转换为一维搜索，大大减少了计算量，并运用由粗到精的层次化思想进一步加速搜索过程。仿真和试验结果表明，建议运用小型五元基阵，可同时兼顾声源定位精度和算法鲁棒性；试验结果表明本文定位算法的整体定位精度良好，且满足实时性要求，可运用于浅水区的目标定位。