基于人工鱼群和粒子群优化混合算法的侧铣刀轴轨迹规划

刘红军 魏宇祥

1.沈阳航空航天大学机电工程学院，沈阳，1101362.沈阳航空航天大学研究生院，沈阳，110136

0 引言

非可展直纹面是工程中的一种常见曲面，主要应用于叶轮类零件，其叶片型面大多数是非可展直纹面和自由曲面。加工此类零件难度较大，一直是数控加工领域研究的难点[1]。侧铣加工采用刀具侧刃进行切削，一次走刀可形成加工表面，具有加工效率高、加工表面粗糙度小等特点。近年来，对非可展直纹面数控加工的研究主要集中在侧铣加工上。

LIU[2]提出了适用于凸自由曲面和直纹面棒铣刀侧铣的单点偏置法及适用于直纹面的双点偏置法、多点偏置法，此方法计算简单，但误差较大；宫虎[3]研究了任意回转面刀具五坐标数控加工的运动几何学基础，证明了设计曲面与刀具包络面的极差等于设计曲面的等距面与刀轴轨迹面的极差，并针对圆锥刀侧铣加工问题，提出了圆柱面与圆锥面转化的思想；ZHANG等[4]对设计曲面、刀具包络面以及刀具曲面三者的关系进行了研究，建立了回转面刀具侧铣非可展直纹面的理论模型；阎长罡等[5]针对圆锥刀侧铣加工问题，结合圆锥面自身的几何特性，提出了法向映射曲线的概念，将刀具包络面向设计曲面的逼近问题转化为每个刀位下法向映射曲线与特征线的最小二乘逼近问题；傅浩杰等[6]针对现有五轴侧铣刀轨生成方法生成组合曲面侧铣加工刀轨困难的问题,通过分析飞机结构件中组合曲面的类型,提出了一种基于曲面拟合的精度可控、刀轴摆动均匀且无干涉的飞机结构件组合曲面侧铣加工刀轨生成方法；胡东方等[7]通过迭代逼近减小初始刀轴矢量误差,将刀轴作为NURBS直纹面母线来重构理论刀轴回归轨迹面，并利用最小二乘法进行进一步优化,建立了弧面凸轮侧铣加工刀轨误差优化模型,提出了求解该优化模型的一种实数编码的人工免疫算法；HSIEH等[8]提出了基于粒子群的五轴数控加工刀具轨迹优化方法，并将智能算法引入到刀具轨迹优化中。

人工鱼群(artificial fish swarm ,AFS)算法[9]是一种有效的寻优算法，具有并行性、简单性、能很快跳出局部极值等优点。但该算法也具有寻优精度不高、后期收敛速度慢等缺陷。

粒子群优化(particle swarm optimization ，PSO)算法是一种基于群智能的演化计算技术，具有概念简单、易于实现、收敛速度快等优点。但该算法极易发生早熟收敛，全局极值的搜索能力差。

本文结合以上两种算法的优点，针对刀具轨迹优化问题确定了单刀位下的误差度量函数，提出了基于人工鱼群(AFS)和粒子群优化(PSO)混合算法的求解策略，并对其进行优化处理得到最优单刀位，进而获得优化后的刀轴轨迹面，并计算得到包络误差。仿真结果验证了该算法具有效率高、求解精度高等优点。

1 初始刀位确定

采用两点偏置法来确定初始刀位，刀具选用圆锥刀，如图1所示。

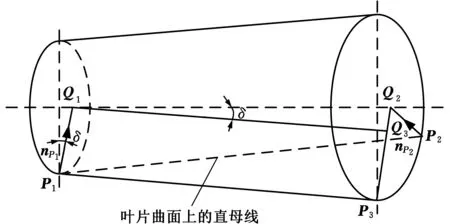
图1 确定初始刀轴矢量Fig.1 Determines the initial cutter axis vector

确定初始刀轴矢量具体步骤如下。

(1)将叶片基线上参数u∈[0,1]离散化(u=u1,u2，…,um)。取参数v=0，u=u1，将该点记为P1；取参数v=1，u=u1，将该点记为P2。

(2)确定刀轴矢量的第一点Q1:

|P1P2|=

式中，(XP1,YP1,ZP1)、(XP2,YP2,ZP2)分别为P1、P2的坐标值；nP1为叶片在P1处的单位法矢；nP2为叶片在P2处的单位法矢(法矢方向在叶片的同一侧)；τ1为P1处沿曲面u方向的切矢；τ2为P2处沿曲面u方向的切矢。

刀轴矢量第一点Q1为

式中，rc为圆锥刀的小端半径；δ为圆锥刀的半锥角。

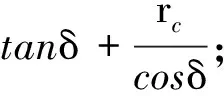
依据上述计算过程，绘制计算初始刀轴矢量流程图，见图2。

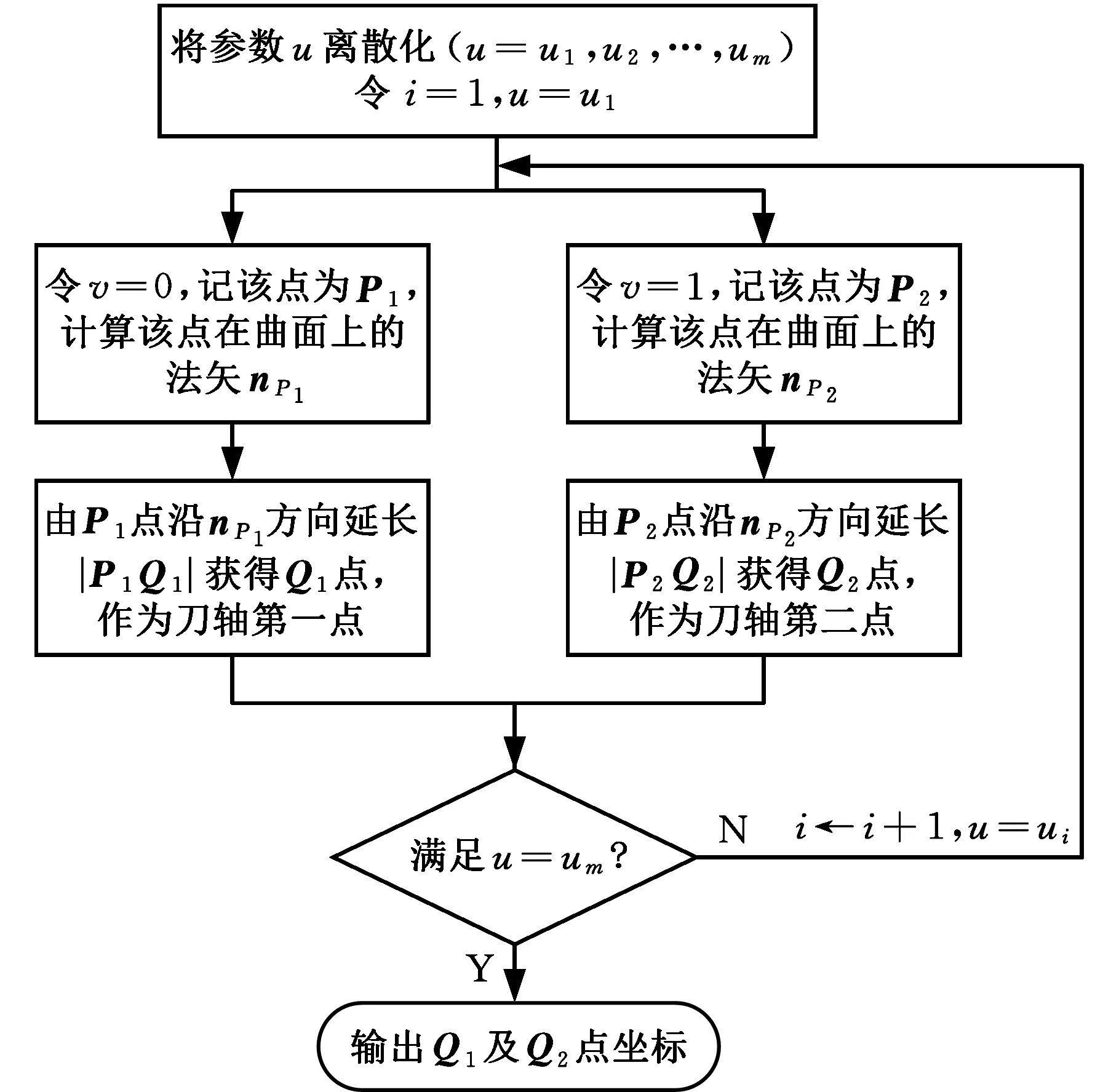
图2 计算初始刀轴矢量流程图Fig.2 Flow chart of the initial cutter axis vector

2 单刀位下的误差度量函数

非可展直纹面直母线各点处的法矢不同，无法用半径大于零的圆柱滚动包络面形成，除非滚动半径为零。真实的加工误差为刀具包络面与设计曲面的法向误差。非可展直纹面的几何特性决定了加工该类曲面有着不可避免的原理性误差，对于每个刀位下，理想状况下有

|PiQi|=r(Pi)i=1,2,…,n

显然，若要使误差减小，就应使||PiQi|-r(Pi)|的值尽可能小，若每个刀位下刀轴上的每一点都尽可能满足上述条件，则得到的刀具包络面会最大限度地逼近设计曲面。

由以上分析可知，单刀位下的误差度量函数如下：

其中，c为刀轴位姿；C为单刀位下所有刀轴位姿的集合；r(Pi)为已知量，因此核心部分是求解|PiQi|(即求解一点Pi到非可展直纹面r(ui,vi)的距离问题)。设垂足坐标(ui,vi)，则垂足点满足以下方程:

(Pi-r(ui,vi))ru(ui,vi)=0

(Pi-r(ui,vi))rv(ui,vi)=0

式中，ru(ui,vi)为Pi点在u方向的切矢；rv(ui,vi)为Pi点在v方向的切矢。

上述方程的解析求解较复杂，不便于计算，本文使用数值法对其进行求解。单刀位的误差度量函数的求解可以看作是一个函数的极小值求解问题，由于函数难以建立明确的函数表达式，用传统方法难以求解，而智能算法在求解该类问题有特别的优势，因此将单刀位误差函数作为智能算法优化的目标函数。

此外，单刀位误差函数的确定对判断单刀位的好坏给出了快捷简便的计算方法。传统方法是通过计算刀具的包络误差，从而判断刀具在某刀位下过切或欠切的情况，计算过程繁琐。相比之下，单刀位误差函数的方法能快速判断刀位是否达到局部最优，计算量小，计算速度快，适合编程处理。在AFS-PSO智能算法中会多次调用误差度量函数，因此，误差度量函数的计算速度对算法效率有重要的影响。

3 基于AFS-PSO算法的刀位优化

3.1 初始种群的生成

初始种群的生成采用如下步骤：①以初始刀轴两端点P1、P2为球心，分别建立半径为R的球形区域，作为初始种群生成区间；②随机在2个球形区域内产生粒子，每个粒子作为刀轴的一个端点，2个粒子作为一个点对，构成了一个新的刀轴矢量，重复上述步骤A次，可构成一个大小为A的矢量数组P=[P[0]，P[1]，…，P[A-1]]；③设刀轴矢量端点坐标Q1(X1,Y1,Z1)和Q2(X2,Y2,Z2)，则矢量数组P中每个元素分别为关于X1、Y1、Z1、X2、Y2、Z2的6维矢量，总计A个6维矢量作为智能算法的初始种群。

成果展示是在任务完成之后，对整个项目完成情况的一次总结评析。这个评估是多元化的，并非传统教师点评，而是存在与学生个人，学生与学生之间，不同小组成员之间，当然也包括教师评价在内的多元的评价方式。在实施项目教学法之前普通话成绩的评定只注重了学生的结果性考核，却忽略了学生的过程性考核。在新的、多元性课程标准中，我们采用了综合评价方法，主要包括普通话水平测试成绩评价、个人口语表达能力评价、团队合租评价、专业实践评价为一体的综合性评价方式。课程以“教师、学生、专业”为一体的多元性评价主体，对学生的普通话课程成绩做出综合性评定。

3.2 基于AFS-PSO算法的优化过程

对于群智能算法而言，群智能是呈现正反馈性质的，如PSO算法中，粒子会偏向于向群体中最好的位置移动。正反馈机制虽然会保证粒子往较好的位置移动，但也会直接导致优化易过快收敛到局部极值，因此，有必要引入抑制过快收敛的机制。AFS算法中拥挤程度概念的引入，避免了群体收敛过快问题的发生。此外，个体能否跳出局部极值也是检验群智能算法性能的要素，通常随机因子是解决跳出局部极值有效的方式，AFS算法中的随机步长，以及PSO算法的速度迭代公式中的随机数和粒子飞行方向都是随机因子，它们的引入保证了算法的全局极值搜索能力。而AFS-PSO混合算法的提出，首先利用AFS算法的全局收敛性快速找到满意的解域,然后利用PSO算法的快速局部搜索能力找到最优值也是基于上述设计原则的考虑。

AFS-PSO混合算法的流程图见图3，具体设计步骤如下。

图3 AFS-PSO算法流程图Fig.3 AFS-PSO algorithm flow chart

(1)初始化种群。对种群内的参数进行设置，如人工鱼的数量、步长、视野、觅食行为的最大尝试次数、拥挤度因子、进化次数等。

(2)公告板初始化。每条人工鱼对应一个刀轴矢量，计算每条人工鱼的适应度值(即单刀位误差度量函数值)，比较这些值，选择其中最小的适应度值，并将该值对应的人工鱼位置赋值给公告板。

(3)鱼群位置更新策略。根据人工鱼的4种行为(觅食、聚群、追尾、随机)来更新自身的位置状态，每次位置更新后计算适应度值并与公告板的适应度值进行比较，若当前适应度值较优，则更新公告板；否则，公告板不变。

(4)鱼群算法终止条件。当鱼群算法达到给定精度时算法终止，即满足

其中，ε为一个足够小的正量，若满足上式条件，则将最优值赋值公告板；否则，转到步骤(3)继续迭代。

(5)赋值粒子群。获取公告板的值赋值gbest，将AFS算法中人工鱼的位置赋值给粒子群，设置淘汰原则，将远离最优位置的人工鱼淘汰;在最优人工鱼附近随机生成若干个粒子，使粒子总数达到N个，赋予每个粒子初始化速度，对每个粒子赋予自适应权重，自适应权重随粒子的目标函数值而自动改变，使粒子向较好的搜索区域靠拢。

(6)适应度值计算。计算每个粒子的适应度值,并与gbest的适应度值进行比较，若当前适应度值较优，则更新当前最优位置赋值给gbest。

(7)粒子状态更新。粒子群算法粒子速度和位置更新表达式分别为

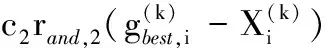
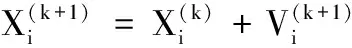
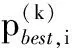
(8)计算更新后粒子的适应度。重新计算每个粒子的适应度值，并与历史值pbest的适应度值进行比较，若当前适应度值较优，则更新pbest值；再将更新的pbest值与群体中最好粒子位置gbest值进行比较,若更新的pbest值较优，则更新gbest值。

(9)更新公告板。重复步骤(7)～(8)，当达到粒子群迭代次数后，将gbest值赋值公告板，并作为最优解输出。

4 包络误差的计算

4.1 圆锥刀圆锥面方程建立

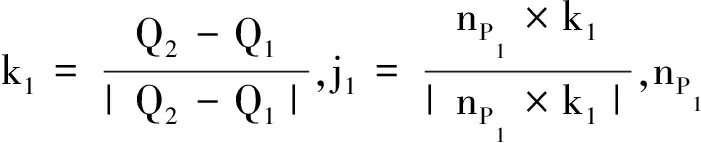
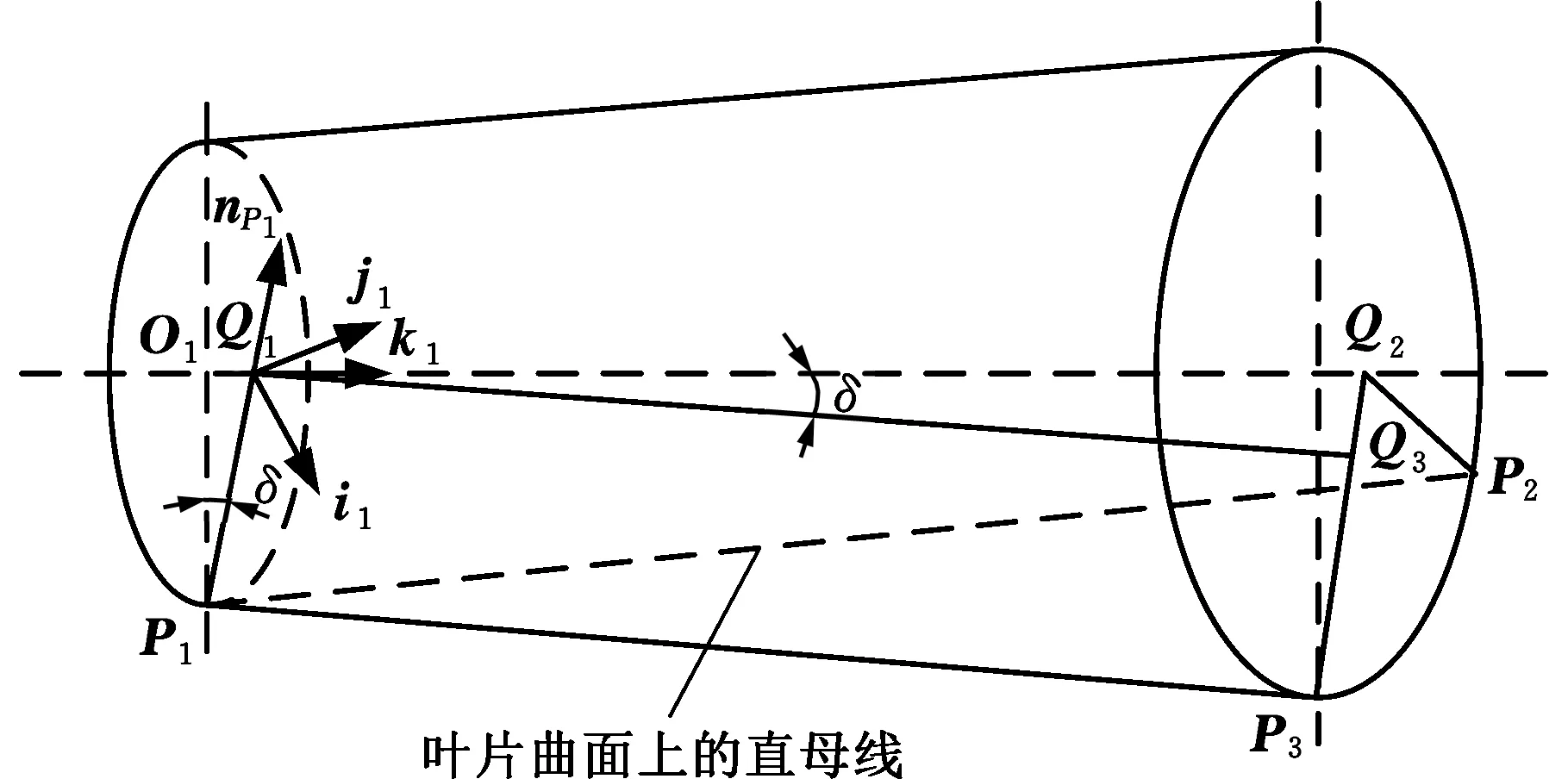
图4 圆锥面方程建立示意图Fig.4 Establishment of cone surface equation

圆锥面在固定坐标系下的方程可表达为

f=O1+(rc+tsinδ)(cosαi1+sinαj1)+tcosδk1

式中，t为圆锥面母线方向的参数；α为转角参数。

4.2 误差模型建立

加工曲面的形成过程就是刀具面族的包络过程，刀具在每个瞬时形成一条切触线，这些切触线的集合形成了加工曲面。

将叶片曲面的某条直母线P1P2均匀离散成若干个点Pi(i=1,2，…，m)，每点处沿其法线方向作射线，被圆锥面截得的长度就是圆锥面在此处的加工误差，用h表示(即包络误差)，即

Pi+hn=O1+(rc+tsinδ)(cosαi1+

sinαj1)+tcosδk1

式中，n为曲面Pi点处的法矢量。

实际上，任意点处的加工误差是由不同位置刀具加工形成的，因此，曲面某点处的加工误差是其射线与不同位置下的刀具圆锥面截得的最小h值，如图5所示。

图5 包络误差说明图Fig.5 Envelope error diagram

5 仿真结果与分析

叶片曲面原始数据来源文献[10]，将叶片曲面划分为28个曲面片，本文以第2曲面片为例(图6)，其2条边界曲线均为非均匀有理B样条曲线，并且具有相同的节点矢量[0，0，0，0，0.2，0.4，0.6，0.8，1.0，1.0，1.0，1.0]，2条B样条曲线相应控制点列于表1中。

图6 叶片曲面模型Fig.6 Blade surface model

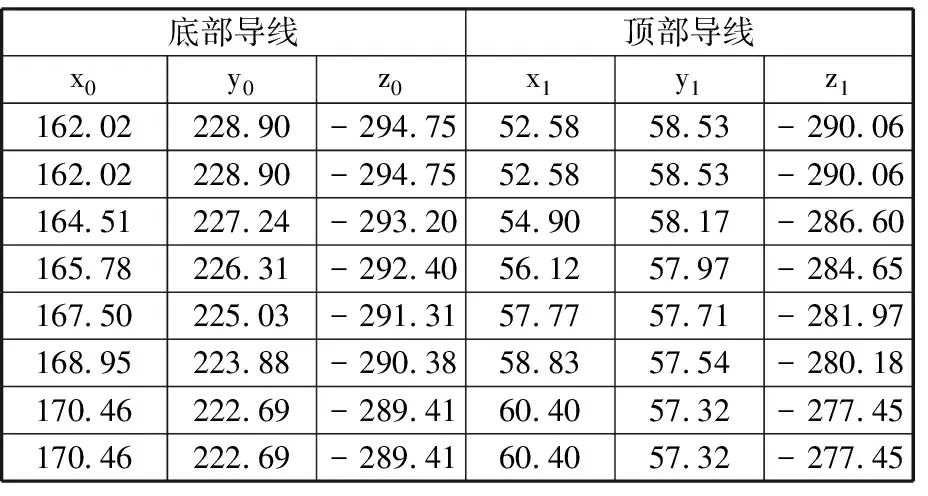
表1 曲面片2边界B样条曲线控制点

选用的圆锥刀小端半径为5 mm，锥顶半角为5°。在曲面片上均匀地选取11个刀位，每个刀具轴线上均匀地选取11个点进行单刀位误差函数的计算。表2给出了u=0位置的单刀位优化结果，其余刀位结果类似。

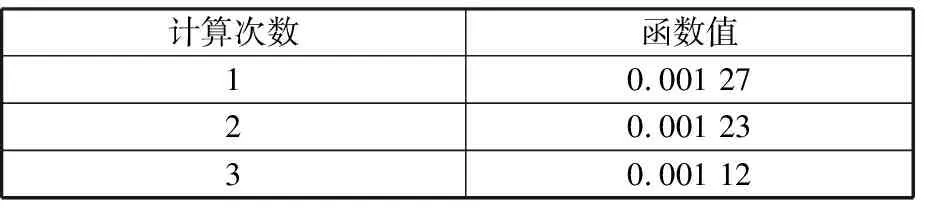
表2 单刀位的优化结果

图7所示为单刀位下全局最优值的收敛情况，优化前后刀具轴迹面边界B样条曲线的控制点分别见表3和表4，优化前后的包络误差分别见图8和图9。

对比图8和图9可以看出，初始轴迹面下的曲面最大极差已达到0.5 mm，而优化后的最大极差为0.038 9mm。

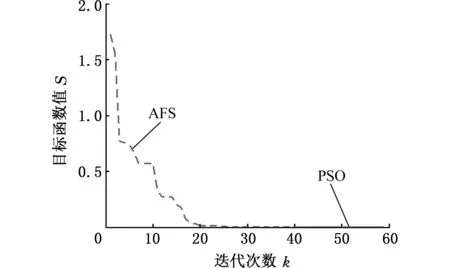
图7 单刀位全局最优值的收敛情况Fig.7 Convergence of global optimum of single cutter

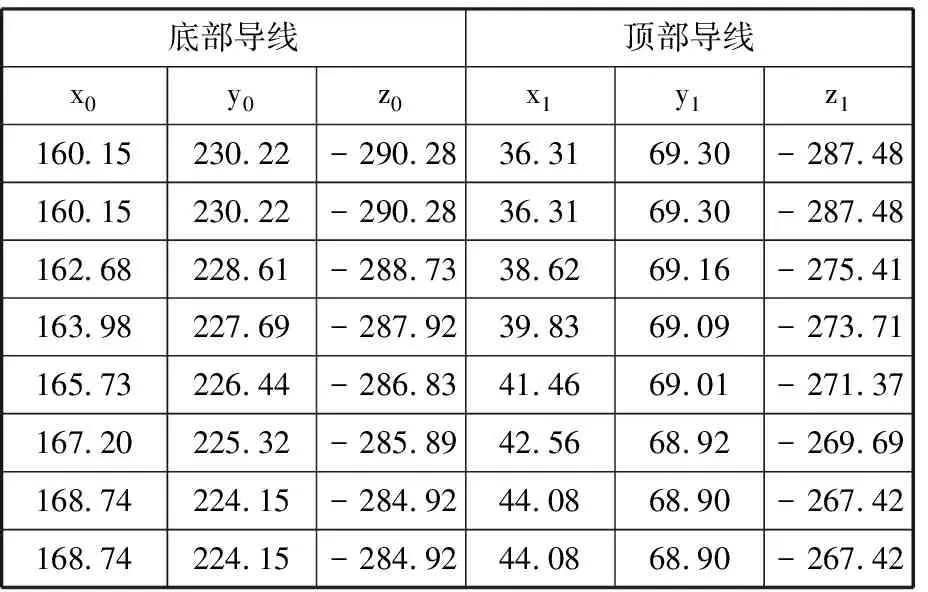
表3 初始轴迹面边界B样条曲线控制点

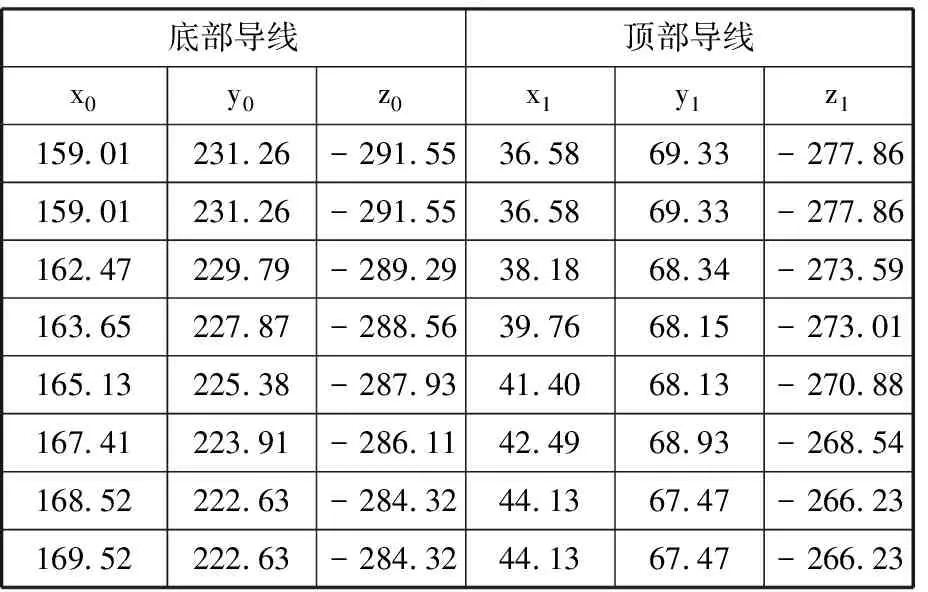
表4 优化后轴迹面边界B样条曲线控制点

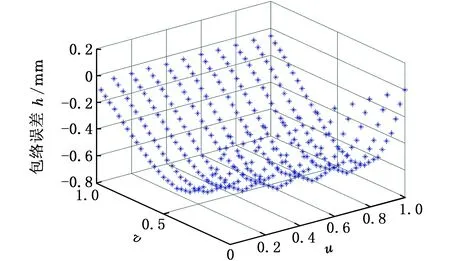
图8 初始包络误差图Fig.8 Initial envelope error diagram

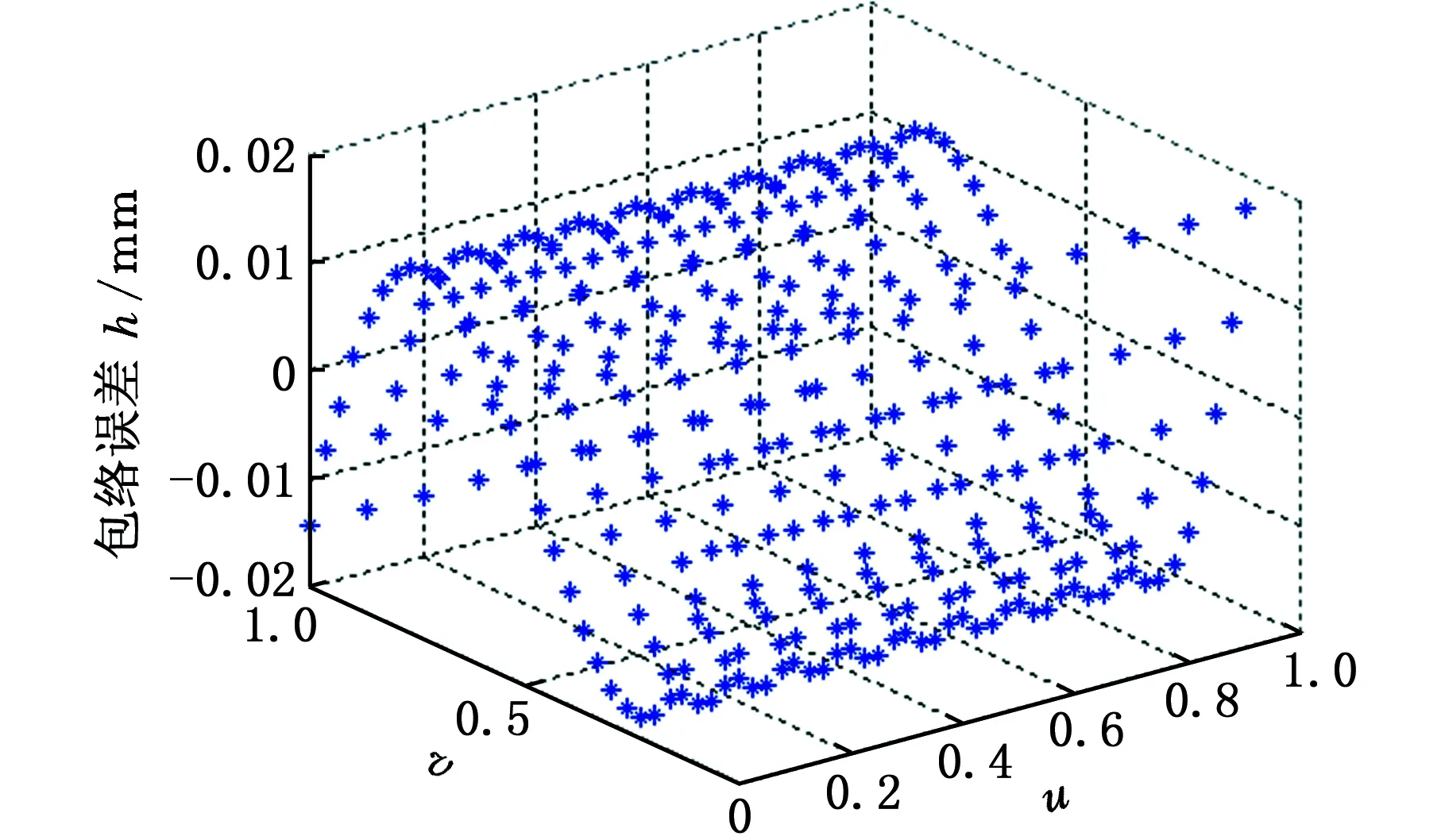
图9 优化后包络误差图Fig.9 Envelope error after optimization

6 结论

(1)提出了单刀位下的误差度量函数，即刀轴上各点到非可展直纹面的距离与对应各点到圆锥面的距离差值的平方和最小。

(2)针对每个刀位下的位姿寻优问题，给出了基于人工鱼群(AFS)和粒子群优化(PSO)混合算法的求解方案。

(3)建立了求解包络误差的模型，仿真结果表明，优化后的刀具包络误差显著减小。