坐标系选取对压制兵器射击准确度的影响分析
张卫民,王 彤,崔 键
(中国兵器工业导航与控制技术研究所,北京 100089)
0 引言
压制兵器以间接瞄准为主要射击方式,作战时需要根据自身的位置和目标的位置,计算目标相对炮位的距离和方向(即炮目距离和炮目方向),以及炮位和目标的高程,进而计算射击诸元。计算距离、方向和高程,就要用到坐标和坐标系。压制兵器作战一般采用绝对坐标系,即某处的坐标值给定后,其在地球上的位置唯一确定。适合炮兵使用的绝对坐标系有两种形式:一是采用以地球参考椭球面为基准的大地坐标系,二是将地球参考椭球表面投影到平面后得到的高斯平面直角坐标系(以下简称平面直角坐标系)。适合炮兵使用的高程有海拔高和大地高,通常采用前者。
由于高斯投影变形的影响,采用平面直角坐标系计算炮目距离和方向时会产生一定计算误差[1-2]。本文分析了采用大地坐标系和采用平面直角坐标系计算炮目距离和方向时的差别,在定量分析高斯投影变形的基础上,给出了针对炮目距离和炮目方向计算误差的修正方法,并给出了计算实例。本文还讨论了高斯投影和UTM投影的关系。
分析结论表明,由于投影变形,在平面直角坐标系下计算炮目距离和方向时对射击准确度有一定的影响,应视情况予以修正,修正后的计算误差可忽略。计算实例表明,炮目距离不大于200 km时,采用平面直角坐标系计算炮目距离和方向并进行修正,是计算炮目距离和炮目方向既快捷又能保证精度的方法。
1 有关参数与定义
1.1 有关参数
地球的形状是一个不规则椭球体,不能用数学公式表达。为分析计算方便,需要确定与地球相近的参考椭球代表地球。参考椭球的形状由其长半轴和短半轴确定,参考椭球面是代表地球的数学表面。在不同历史时期、根据不同的测量数据、采用不同的方法,科学工作者推算出的参考椭球参数也有所不同。
参考椭球的有关参数包括:椭球长半轴a,椭球短半轴b;第二偏心率;表1为有关参考椭球长半轴a和短半轴b的取值。
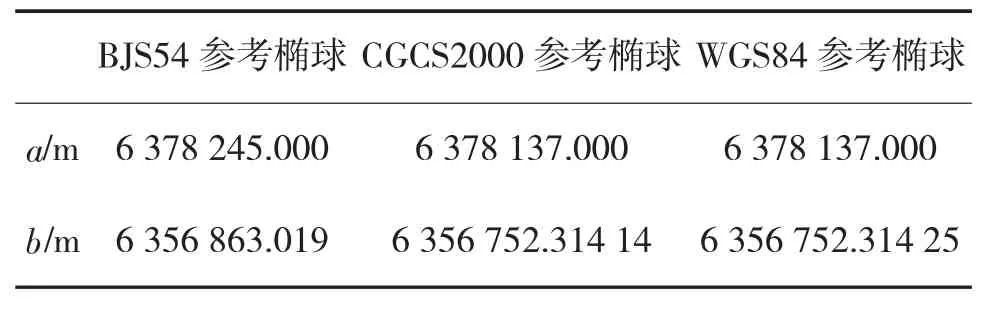
表1 参考椭球参数
1.2 有关定义
1)子午面和子午线。参考椭球的子午面为包含椭球旋转轴(短轴)的平面,子午线为子午面与椭球面的截线。
2)赤道面和赤道。参考椭球的赤道面为通过椭球中心且垂直于旋转轴的平面,赤道为赤道面与椭球面的截线。
3)大地坐标系。大地坐标系采用大地经纬度描述参考椭球表面任意点的位置。纬度是该点的法线与赤道面的夹角,向北为正称为北纬,向南为负称为南纬。经度为该点子午面与起始子午面的夹角,由起始子午面起算,向东为正称为东经,向西为负称为西经。
4)平面直角坐标系。将椭球面按经度6°或者3°分带(炮兵通常用6°分带),通过高斯投影获得的平面直角坐标系为平面直角坐标系。中央子午线的投影为x轴,向北为正。赤道投影为y轴,向东为正。为了避免横坐标出现负号,并对各带的坐标加以区别,规定在y值加上500 000 m的基础上,再在前面冠以代号。这种坐标称为“通用坐标”[3](也称为“国家统一坐标”[2]或“假定坐标”[4])。在实际计算中,y值不加500 000 m,也不冠以带号,称为自然坐标。
5)大地线。参考椭球表面两点之间最短的连线,其长度即两点之间的距离。
6)大地方位角。椭球表面线段与子午线的夹角,以正北为基准方向。
7)坐标方位角。平面直角坐标系下线段与x轴的夹角,以坐标北为基准方向。
8)子午线收敛角。平面直角坐标系下子午线投影与x轴的夹角。
2 炮目距离和炮目方位角计算
炮目距离指炮位与目标之间的水平距离,即炮目连线投影到水平面之后的长度。由于地球表面为椭球面,因此,在距离较远、地球表面曲率不能忽略时,炮目水平距离实际上是炮目连线投影到大地水准面之后的长度,即大地水准面上的球面距离。因为大地水准面处处与重力方向垂直,所以炮目连线投影到大地水准面之后虽然不是直线,但处处是“水平”的。设P1点为炮位,P2点为目标,则投影到大地水准面之后的炮目水平距离如图1所示。
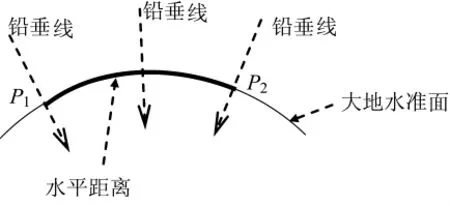
图1 水平距离示意图
由前面的定义,大地线的长度为参考椭球表面的距离,而上述水平距离为大地水准面上距离,二者略有差别。由于大地水准面为略有起伏的不规则曲面,不能用数学公式表示,大地水准面上的距离也不能精确计算;另一方面,对于压制兵器而言,大地线长度与水平距离之间的差别可以忽略(只有长距离精确惯性导航时才能体现该差别[4])。因此,在以下讨论中认为大地线长度与水平距离相同。
2.1 平面直角坐标系下求距离和方位角
因为投影变形的影响,使用平面直角坐标系会产生一些计算误差[1]。设P1和P2在平面直角坐标系中的坐标分别为(x1,y1)和(x2,y2),并有
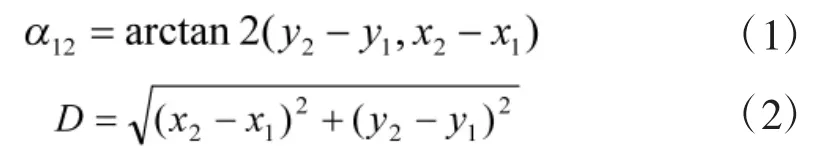
式中,arctan2表示值域为4个象限的反正切函数。
若P1点为炮位,P2点为目标,则上两式求出的即为平面直角坐标系下的炮目坐标方位角和炮目距离。
由于投影变形,式(1)得到的α12与真实的炮目坐标方位角相差方向改化δ,式(2)得到的D与真实的炮目距离S(两点间大地线)也相差距离改化[1]。
2.1.1 高斯投影方向改化计算
根据高斯投影的特性,离中央子午线越远,投影变形越大,方向改化δ也越大。δ可由下式近似求得[2]。
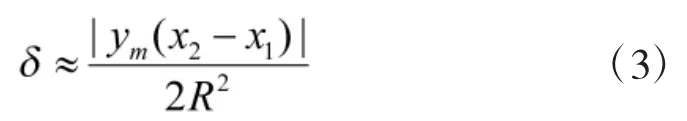
取R=6 370 km,由式(3)可得δ的概略数值如表 2(δ的单位为密位(mil))。
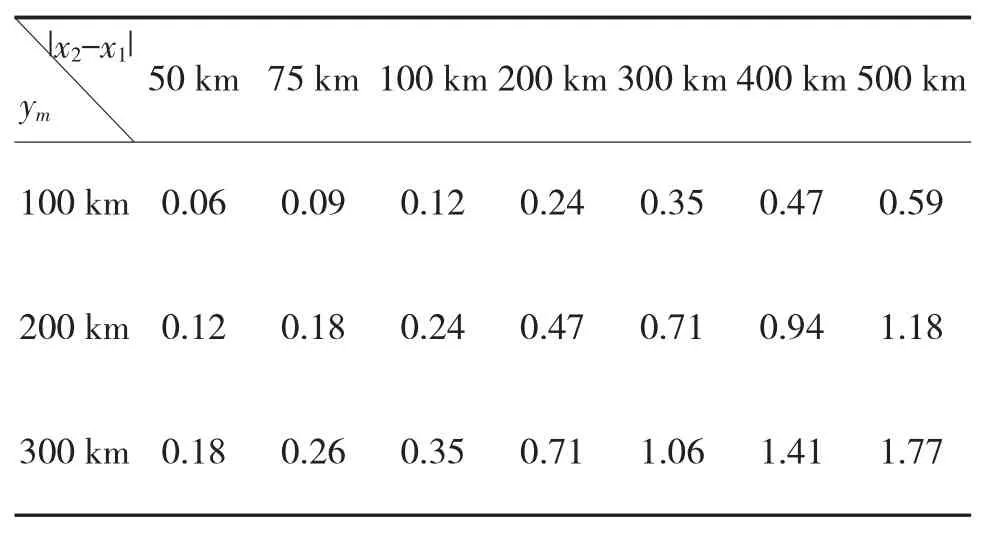
表2 高斯投影方向改化δ参考值
由表2可知,在离中央子午线较远且南北方向距离较大时,方向改化δ可大于1 mil。
2.1.2 高斯投影距离改化计算
高斯投影距离变形的程度可用投影长度比表示。设dS为大地线S在某点的微分弧长,ds为dS的投影弧长,则m=ds/dS为该点投影的长度比。由于高斯投影为正形投影,因此,长度比m仅与该点的位置有关,与方向无关。若该点的纬度为B,经度与投影带中央子午线之差为l,则该点的投影长度比m可由下式近似求得[2]。
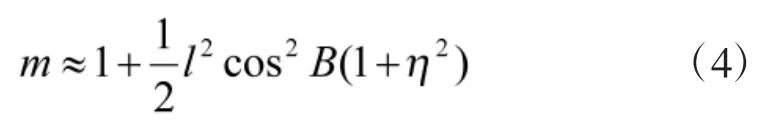

表3 高斯投影长度比m参考值
由表3可知,在一定范围内,m近似为常数,此时有
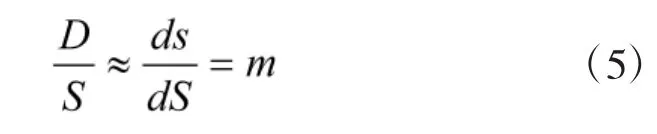
即平面直角坐标系下求得的距离D与实际距离(大地线S)的比值为m。由表3可知,在投影带的边缘且纬度较低时,投影变形引起的距离误差可大于1‰,对应炮目距离100 km、300 km、500 km的情况,平面直角坐标系下求得的距离D与实际距离S可分别相差100 m、300 m、500 m以上。
2.2 高斯投影变形的影响分析
根据前面的分析,在平面直角坐标系下求炮目方向和距离时,由于投影变形的影响,会产生计算误差。与中央子午线的经差越大,即越靠近投影带边缘,误差越大;经差相同时,纬度越低,误差越大。显然,当炮位与目标分别处在两个相邻的投影带,需要通过“坐标换带”计算炮目方向和距离时,换带后的坐标离中央子午线最远,因此,计算误差最大。
炮目方向和距离的计算误差属于系统误差,当压制兵器发射常规弹药或惯性制导弹药时,将对射击准确度产生影响。
2.2.1 发射常规弹药时的影响
炮目方向和距离是计算射击诸元的必要条件,因此,其计算误差是诸元计算误差(算法误差)的组成部分,直接影响到射击诸元的计算精度。设Eh为横向射击诸元的计算误差,Ez为纵向射击诸元的计算误差;炮目方向和距离的计算误差分别为Ehj和Ezj,则参照“微小误差取舍准则”[5],当 Ehj≤Eh/3 和Ezj≤Ez/3时,炮目方向和距离计算误差的影响方可忽略。
压制兵器射击诸元计算精度的指标通常是横向为0.5 mil(中间误差),纵向为0.4‰D(中间误差,D为炮目距离);换算为标准误差后分别大约为0.75 mil和0.6‰D。因此,炮目方向计算误差应控制在Ehj≤Eh/3≈0.25 mil,炮目距离计算误差应控制在 Ezj≤Ez/3≈0.2‰D。
由表2易见,用平面直角坐标系计算炮目方向的误差一般情况下较小,当炮目距离小于50 km时,此误差可忽略;随着炮目距离增加,该误差会超过0.25 mil,应视情况予以修正。
由表3易见,在1/3以上的区域中,投影长度比大于1.000 2,即用平面直角坐标系计算炮目距离的误差超过0.2‰D,最大可大于1‰D,应视情况予以修正。
2.2.2 发射惯性制导弹药时的影响
对于惯性制导的弹药,其制导过程就是在弹体飞行过程中,弹载惯性导航控制系统实时测量、解算弹体的位置、方向和姿态,据此控制弹体朝设定的方向(即炮目方向)飞行设定的距离(即炮目距离)。因此,炮目方向和距离的计算误差是弹体落点误差的组成部分,直接叠加在弹体落点误差上。
惯性制导弹药的落点精度主要由弹载惯性导航控制系统决定,其导航控制的精度越高,落点误差越小。显然,若假设弹载惯性导航控制系统自身的误差为零,则惯性制导弹药的落点误差取决于炮目方向和距离的计算误差。
因此,相对于发射常规弹药(此时压制兵器的射击准确度主要取决于射表、气象等因素),炮目方向和距离的计算误差对惯性制导弹药的射击准确度影响更大,特别是对于高精度的惯性制导弹药。
2.3 计算误差的修正方法
2.3.1 炮目方向计算误差修正
炮目方向计算误差的修正值即方向改化值,可由式(3)求得。由于方向改化值可能为正也可能为负,因此,需要特别注意其符号。

其中
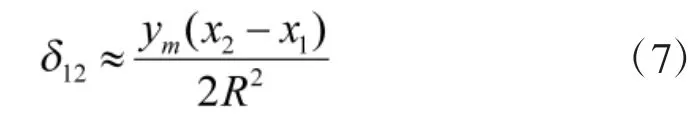
上式中各变量与式(3)相同。
关于方向改化公式的推导详见参考文献[2]。此处为使计算所得的δ永远加到计算的坐标方位角α12之上,所以式(7)定义的δ的符号与参考文献[2]中相反。
2.3.2 炮目距离计算误差修正
设式(2)求得的炮目距离为D,真实的炮目距离为 S(大地线),则由式(5)有

其中,m为线段上的平均投影长度比,可由下式求得[2]

式中,R和ym与式(7)相同。关于距离改化公式的推导详见参考文献[2]。
若遇到y1与y2符号相反(即P1和P2点分别位于中央子午线两侧)的情况,投影长度比需要分段计算,此时式(8)修正为
其中
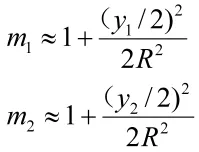
2.4 大地坐标系下求距离和方位角
大地坐标系是椭球面坐标系,没有投影变形。在大地坐标系下求炮目距离和炮目大地方位角,可以保证计算精度。
椭球面上点的大地经度L、大地纬度B,两点间的大地线长度S及正、反大地方位角A12、A21,通称为大地元素。如果知道某些大地元素推求另一些大地元素,这样的问题称为大地主题解算,大地主题解算有正解和反解。
已知 P1点的大地坐标(B1,L1),P1至 P2的大地线长度S以及大地方位角A12,计算P2点的大地坐标(B2,L2)和大地线 S在 P2点的反大地方位角 A21,这类问题称为大地主题正解。
如果已知 P1和 P2点的大地坐标(B1,L1)和(B2,L2),计算P1至P2的大地线长度S及其正、反大地方位角A12、A21,这类问题称为大地主题反解。在大地坐标系下求炮目距离和炮目大地方位角,属于大地主题反解问题。
2.4.1 计算方法
由于大地线的数学表述比较复杂,大地主题解算的方法一般也比较复杂。大地主题解算的方法有许多种,主要有高斯平均引数公式、巴乌曼投影公式、贝塞尔公式和文森特公式等,其原理都是将椭球面上特定曲线微分方程展开不同形式的幂级数,或者直接利用数值积分算法,从而实现积分运算,求解出各大地元素[2,4,6]。但是这些公式中普遍存在以下问题:一是奇异问题,即当两点位于同一子午圈、赤道或极点上时,算法不能解算;二是有些解算公式需要繁琐的象限判断;三是应用范围受限。
文献[6]在综合上述解算公式优缺点的基础上,应用球面三角原理和文森特公式嵌套系数思想,兼顾计算机数值计算的应用,重新推算大地主题解算过程,提出正算和反算的“大地主题解实用算法”。该算法无奇异、适用任意距离,且精度高(毫米级)。文献[7-8]也结合工程实际对文森特公式进行了补充和完善,给出了符合工程化运用需要的改进算法。
考虑到炮兵作战并不要求非常高的计算精度,也可采用大椭圆法解大地问题[4]。该方法相对简单些。所谓大椭圆,就是通过椭球面上两已知点和该椭球中心所作的平面与椭球面的交线。椭球表面两点之间的大地距离可近似用椭球面上的大椭圆弧来代替。经验证,用上述大椭圆法求距离的精度为米级(距离为2 000 km时的计算实例,误差为1.27 m)[4],可以满足炮兵作战的需求。
2.4.2 与平面直角坐标系比较
与平面直角坐标系相比,在大地坐标系下求炮目距离和炮目方向虽然计算稍复杂,但无投影变形,也无坐标跨带问题,保证了计算精度。
在平面直角坐标系下计算的方位角为坐标方位角,在大地坐标系下计算的方位角为大地方位角,前者以坐标北(X轴)为基准,后者以真北(当地子午线)为北向基准,二者相差子午线收敛角。
3 计算实例
3.1 例题
设 PA、PB、PC、PD各点在 CGCS2000 坐标系统中的 大 地 坐 标 分 别 为 BA=30°0'0'',LA=107°45'0'';BB=30°30'0'',LB=107°45'0'';BC=30°0'0'',LC=108°45'0'';BD=31°30'0'',LD=108°15'0'';
由高斯投影公式求得的上述各点在平面直角坐标系中的坐标分别为

括号中为自然坐标(下同)。
在以下各例题中,P1点为炮位,P2点为目标。
例1:令P1=PA,P2=PB,炮位与目标在投影带(18带)东侧,相距55 km。
例2:令P1=PC,P2=PD,炮位与目标在投影带(19带)西侧,相距173 km。
例3:令P1=PB,P2=PC,炮位与目标在不同投影带,相距111 km。
由于P1在18带,P2在19带,因此,需要坐标换带。由高斯投影公式,将P2(即PC)投影到18带,可得
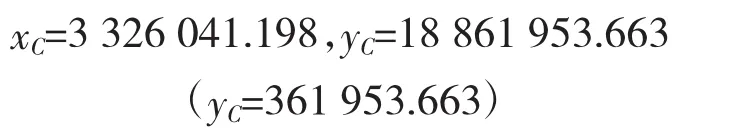
例4:令P1=PD,P2=PA,炮位与目标在不同投影带,相距173 km。
由于P1在19带,P2在18带,因此,需要坐标换带。由高斯投影公式,将P2(即PA)投影到19带,可得
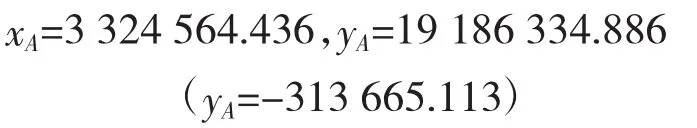
3.2 计算结果分析
3.2.1 关于炮目距离的计算
上述4个例题中关于炮目距离的计算结果见下页表4。
在例1和例2中,由于炮位和目标的位置离中央子午线较远,因此,高斯投影变形引起的炮目距离计算误差较为显著;在例3和例4中,由于炮位、目标坐标跨带,此误差更为显著。采用2.3中的方法对计算结果进行修正后,高斯投影变形引起的距离计算误差(小于1 m)可忽略。
3.2.2 关于炮目方向的计算
上述4个例题中关于炮目方向的计算结果见表5。
由坐标方位角、大地方位角和子午线收敛角的关系,有α12=A12-γ,据此可得表5中炮目坐标方位角计算误差Δα12的计算公式
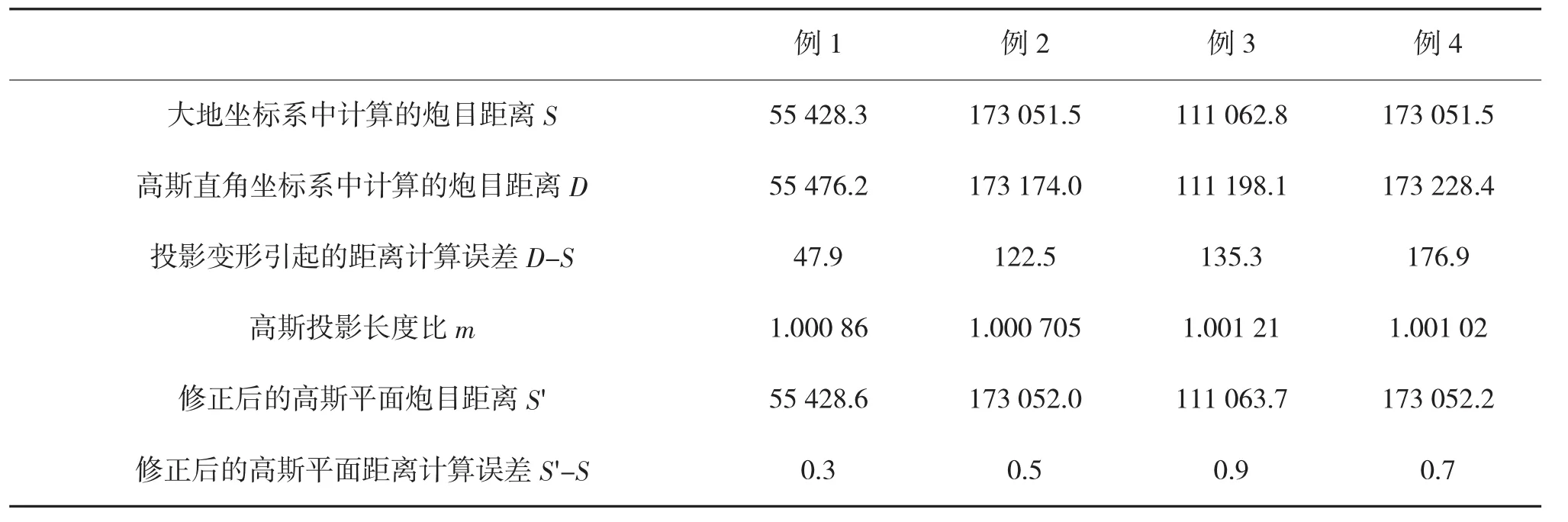
表4 有关炮目距离的计算结果(单位:m)

表5 有关炮目方向的计算结果(单位:mil)
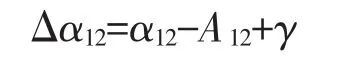
同理,修正后的坐标方位角计算误差为
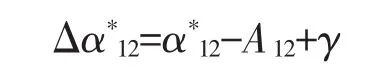
在例2和例4中,由于炮位和目标在南北方向上相距较远(即|x2-x1|较大),因此,高斯投影变形引起的坐标方位角计算误差较为显著;其他两例中,该项误差也接近0.2 mil。采用2.3中的方法对计算结果进行修正后,该计算误差可忽略。
4 WGS84坐标系统和UTM投影
4.1 概述
WGS84世界大地坐标系统是国际上采用的一种坐标系统,GPS定位即采用此坐标系统。WGS84参考椭球的参数与CGCS2000参考椭球基本相同,因此,空间某一固定点在WGS84和CGCS2000中的大地坐标(经纬度和大地高)一致(误差小于1 mm)。
UTM投影即通用横轴墨卡托投影(Universal Transverse Mercator Projection),由美国军事测绘局于1938年提出,1945年开始应用,目前已被许多国家和地区采用。从几何意义上讲,UTM投影属于横轴等角割椭圆柱投影,投影后两条割线上没有变形,中央子午线投影长度比为0.999 6,其他特性与高斯投影相同。
4.2 UTM投影与高斯投影的关系
高斯投影是椭圆柱横正轴切地球椭球体正形投影,UTM投影是椭圆柱横正轴割地球椭球体正形投影。前者投影后中央子午线长度不变,自中央子午线向两侧投影带边缘变形逐渐增加;后者中央子午线投影长度比为0.999 6,向两侧随着距离增大,投影后的长度比逐渐增大,两条割线投影的长度比为1,没有变形,离割线越远变形越大;两条割线之间投影变形为负值,两条割线之外投影变形为正值[8]。
与高斯投影相比,UTM投影使中央子午线投影后缩短0.4‰,从而控制投影长度比在6°投影带内小于1.001,即最大变形小于1‰,改善了投影带内投影长度变形分布。而高斯投影在6°投影带内最大变形可达 1.4‰(B=0°,l=3°处)。
高斯投影与UTM投影的自然坐标(未平移之前不加带号的坐标)之间有一个简单的比例关系,即xUTM=0.999 6xGauss,yUTM=0.999 6yGauss。所以通过高斯投影公式计算出高斯投影坐标后,乘以比例因子可获得UTM投影后的平面直角坐标。
由以上讨论可得出如下推论:设P1和P2为同一参考椭球表面的确定点,分别在UTM投影直角坐标系和高斯投影直角坐标系中求距离和坐标方位角,则前者求得的距离是后者的0.999 6倍,二者求得的坐标方位角相同。
5 结论
本文在定量分析高斯投影变形的基础上,给出了针对炮目距离和方向计算误差的修正方法,并讨论了高斯投影和UTM投影的关系。
根据本文的分析,可以得到如下结论:
1)由于投影变形,在平面直角坐标系下计算炮目距离和方向时对射击准确度有一定的影响,若发射非制导弹药或惯性制导弹药(特别是后者),应视情况予以修正;
2)计算实例表明,炮目距离不大于200 km时,采用平面直角坐标系计算炮目距离和炮目方向并进行修正,是计算炮目距离和方向既快捷又能保证精度的方法,修正后的计算误差可以忽略;
3)在大地坐标系下求炮目距离和炮目方向虽然计算稍复杂,但无投影变形,也无坐标跨带问题,在炮目距离较远时可优先考虑。

