两面投影三角形的形体构形分析

张春艳，李玉梅

（蚌埠学院 机械与车辆工程学院，安徽 蚌埠 233030）

两面投影三角形的形体构形是创造性三维构形的重点与难点之一，现有教材和研究文献都作了不同程度的论述，如：三视图中若有两个视图的外形轮廓为三角形，该基本体为“锥"[1]；含有同面点集的两面单框三角形的最大公共点群域是四棱锥体[2]；垂直于同一轴线的两面对应投影直线被定义为同面点集，同面点集为可构投影[3]。但是，由于“教"与“研"之间衔接不良、三角形组合之间构图方式的不断变化和创新，对现有部分构形设计的规律提出了更高的挑战，结果直接影响了构形设计质量和效率。这里选择含有平线（与投影轴平行或垂直）的两面投影三角形作为分析对象，对两面单框三角形、多框三角形组合与形体之间的互译，进行逻辑推理并结合“大胆假设，小心求证[4]"的过程分析，系统梳理两面投影三角形的形体构形分析依据，提高文献资料之间的互动性，并在此基础上总结规律，达到以不变应万变、举一反三的目的。

1 两面单框三角形的形体构形

1.1 含有同面点集的两面单框三角形的形体构形

图1所示三组V-W投影均由两条平线和一条斜线组成的直角三角形图框，其中处于水平位置的一对平线垂直于oz坐标轴，构成一对同面点集，则该两面投影的空间最大点集域是以处于水平面的长方形（含正方形）A1B1C1D1为锥底，并以三角形图框的第三个顶点为锥顶的四棱锥，如图1（a）中的B-A1B1C1D1、图1（b）中的C-A1B1C1D1和图1（c）中的A-A1B1C1D1。

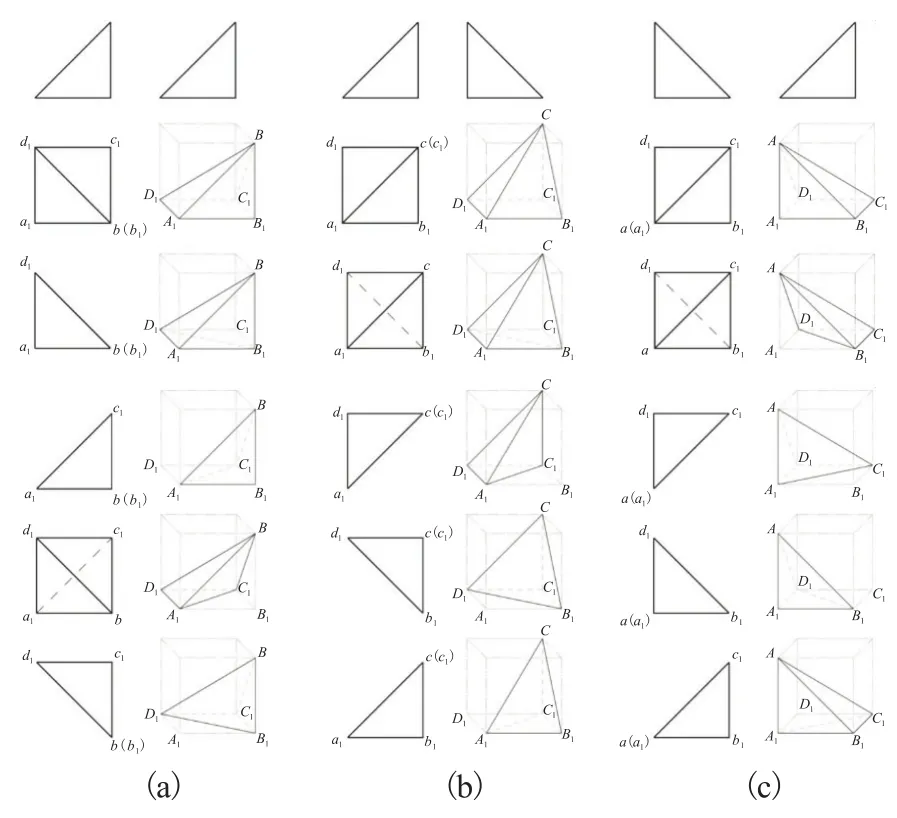
图1 V-W投影直角三角形对应的四棱锥和三棱锥

根据左右、前后空间方位关系，在含有四个点的底平面A1B1C1D1内，构成棱椎体的几何元素至少包含其中三个点（只有两个点时对应空间二维三角形）。依次用排除法去掉某一个点后可以构造出互补成四棱锥的三棱锥，如图1（a）中的BA1B1C1D1=B-A1B1D1+B-B1C1D1=B-A1B1C1+B-A1C1D1，均完全符合题设条件，则H面投影反映了底平面的实形及其点A1、B1、C1和D1之间的排列组合位置关系。同理，图1（b）和图1（c）中的互补三棱锥都满足题设条件。B-A1B1C1D1、C-A1B1C1D1和AA1B1C1D1为同一结构形状却处于不同位置的四棱锥 ，B-A1B1D1、B-B1C1D1、C-A1C1D1、C-A1B1C1、AA1C1D1、A-A1B1C1，B-A1C1D1、C-A1B1D1和A-B1C1D1为同一结构形状却处于不同位置的三棱锥，BA1B1C1、C-B1C1D1和A-A1B1D1亦处于不同位置却是同一结构形状的三棱锥。

将同面点集对应的空间矩形或三角形具有可构性的边线由直线转换为含有凹凸形状特征的曲线，也可以构成一系列含有凹凸面的椎体如图2。

图3（a）所示V-H投影[5]等腰三角形的一对右边线长度相等且垂直于ox坐标轴，对应空间最大点集域是以处于侧平面的正方形为锥底的四棱锥见图3（b），则同一结构形状三棱锥的位置特征见图3（c）～（f）。同理，对含有同面点集的侧平面进行平曲、凹凸组合可构造出含有曲面的椎体如图4（a）～（e）。

1.2 不含有同面点集的两面单框三角形形体构形

图2 同面点集范围内凹凸形状特征构形

图3 V-H投影等腰三角形对应的棱锥体

图4 同面点集对应含有曲面的部分椎体

图5（a）可以看作是将一平面正方形沿其对角线拆分而成的V-W投影三角形，形成两对平线和一对互相平行的斜线，其空间分析模型属于正方体，但一定不含有端点B、C、C1和D1，且一定含有铅垂线AA1、正垂线AD和侧垂线A1B1，△ADA1是侧平面，△AA1B1是正平面，则题设中的对应三角形图框是形体上两个不同外表面的投影（平行面）；斜线d'b1'和d"b1"为正方体中的体对角线DB1，斜线（a'）d'b1'与三角形图框a"d"b1"对应，斜线d"（a1"）b1"与三角形图框d'（a1'）b1'对应，则包含一般位置直线DB1的△ADB1和△A1DB1分别为正垂面和侧垂面。因此满足投影条件的形体表面的类属形状和位置均属定形投影，即唯一确切地表达四面体ADB1A1。

图6（a）所示V-H投影等腰三角形中含有一对平线和两对斜线。平线对应铅垂线EE1和正垂线GF，其端点E、E1、G和F分别为定点，唯一确定空间四个三角形平面的性质和位置，即分别有两个铅垂面△GEE1和△FEE1，以及两个正垂面△GFE和△GFE1，这就决定了四面体EE1FG为定形投影如图6（b），因此题设中的对应三角形图框是四面体中两个外表面的投影且具有可逆性。

分析两面单框三角形的形体构形，可得如下结论：

（1）棱柱体、棱锥体成为两面投影三角形的形体构形中重要的两种分析模型；任何一平线可能对应模型表面中的棱线（垂直线）、面对角线（平行线）或平行面的投影，而任意一斜线的空间位置或类型可能对应模型的面对角线（平行线）、体对角线（一般直线）或垂直面的投影。

（2）同面点集对应锥底平面中的端点和边线的位置和数目均可构，对应锥底平面的位置特征和形状特征具有可构性，锥面形状随锥底平面或

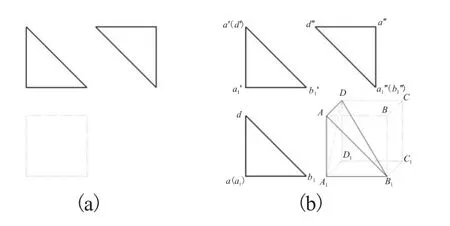
图5 不含有同面点集时的V-W投影直角三角形的形体构形

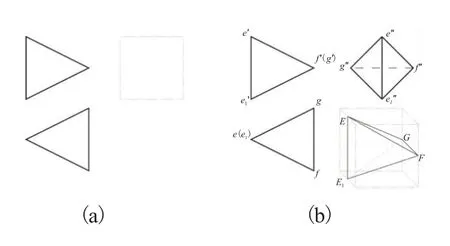
图6 不含有同面点集时的V-H投影等腰三角形的形体构形

平行线实形特征的变化亦具有可构性，但锥曲面中凹凸形状特征的投影不能在三角形图框内产生线；三角形图框对应椎面的实形、类似形或同一个外表面投影、两个外表面的投影组合，且待构形的形体可以是处于不同空间位置同一个锥体。

（3）在含有平线但不含有同面点集的条件下，两面单框三角形具有可逆性且均为平面体。

2 两面多框三角形构图方式及其形体构形

2.1 同形两面多框三角形组合的形体构形

2.1.1 形状和方向均相同的两面多框三角形

图7（a）所示V-H投影[6]的外轮廓为正方形，左右两边线作为大小相等且相互平行的同面点集，对应空间最大点群域为正方体；方向相同且与同面点集两端点相交的一对斜线将正方形分成两对三角形图框，构成形状、方向和大小均相同的两面两框三角形组合，其形体构形应在正方体内，根据投影特性判断斜线的空间位置或类型：（1）斜线作为正方体的面对角线如图7（b），满足投影条件；（2）当斜线作为正方体的体对角线时，含有该斜线且公用正方体棱线和面对角线的三角形图框，一定含有投影面垂直面，其中存在同一三面投影对应两个以上切割体，这是由于截交线位置特征和形状特征的投影重合形成的可构三视图[7]如图7（c）～（f），则V-H投影为类似形互补[8]或类似形与实形构成的三角形组合。因此，同面点集对应的空间二维几何形均具有平曲、凹凸形状特征的可构性。

图8所示V-W投影的外轮廓为三角形，内部嵌套相交另一对三角形图框，且分别含有一对同面点集，内外斜线均与两对同面点集相交，其形体构形一般应作为内图框切割外图框而成的切割体如图7（a）～（c），或内外图框叠加组成的叠加体如图7（d）～（e）。

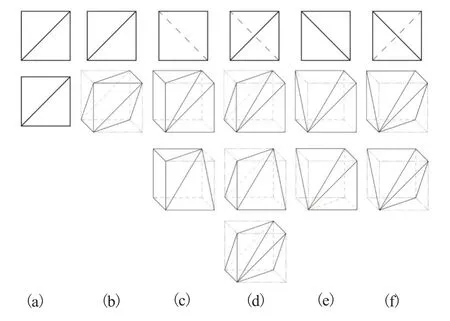
图7 V-H投影中斜线方向相同时对应的部分平面切割体

图8 V-W内外三角形嵌套相交时对应的部分形体

2.1.2 形状相同且互为倒置的两面多框三角形

图9所示V-W投影[9]在oz坐标轴方向对称，即斜线虽然分别与同面点集的两个端点相交，但斜线作为投影外轮廓正方形的对角线方向是相反的，其形体构形与图7中判断斜线的过程类似，得到待构形的部分切割体如图9（a）～（e）。但不同的是，作为同面点集对应正方形下边线中的直线A1B1和A1D1为可逆几何元素，与其相关联的△A1B1B和△A1D1D分别是不可构的投影面平行面；其余边线或切割体的表面具有平曲、凹凸形状特征的可构性。

图10所示V-W投影[10]的外轮廓正方形内部的两条相交斜线将V面投影正方形分成左、中、右三个三角形图框，而对应W面投影正方形分为后、中、前三个三角形图框，把V、W投影分别按“左对应（组合）后”、“中对应（组合）中”、“右对应（组合）前”的投影方位对应关系，得到部分平面切割体如图10（a）～（e）。对应一系列含有锥曲面特征的部分形体如图10（f）～（j）。此时，不含有同面点集的内部三角形——“中对应（组合）中”具有位置特征和形状特征的可构性。

2.2 同类形两面多框三角形组合的形体构形

2.2.1 图框数目相等的同类形两面多框三角形

图11中的V面投影外轮廓为正方形，W面投影外轮廓为上大下小的等腰梯形，斜线分别与两对同面点集相交，构成V-W投影中分别含有三个三角形图框。其中，上边线存在一对大小相等的同面点集，而下边线为一对大小不等的同面点集。因此其形体构形与图10中按照投影方位对应组合关系，构造出的平面切割体如图11（a），同面点集对应形状特征变化的部分切割体如图11（b）～（e）。

图12所示V-H投影由三对三角形图框组成，且外轮廓的左右两边线含有两对同面点集，具有平曲、凹凸形状特征的可构性。点C在外轮廓对应最大空间点集域为四棱柱的最上、右、后，平线对应斜线ef，则E1F1为水平线且具有可逆性，CE1和CF1均为一般位置直线且亦具有可逆性。因此，△ce1f1和虽然属于对应三角形图框，但属于定形投影且为一般位置平面。其余两对三角形图框中均含有同面点集，与一般位置直线CE1和CF1公用的平面可能是垂直面或一般位置面，结合四棱柱中的平行面、棱线和面对角线，截交线均为直线的部分平面切割体如图12（a）～（e）。

2.2.2 图框数目不等的同类形两面多框三角形

图13（a）所示V-H投影[11]外轮廓为正方形且含有两对同面点集，其中V面投影有三个三角形图框，H面投影有四个三角形图框。△efc对应平线，则△EFC为水平面，反映实形且为不可构表面；为对应三角形图框，为一般位置平面亦为不可构表面，其余两对对应三角形图框均含有同面点集。因此，在同面点集范围内进行位置特征、形状特征构形的部分形体如图13（b）～（f）。

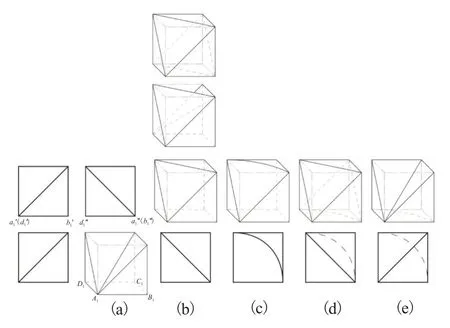
图9 V-W投影中斜线方向相反时的部分切割体

图10 形状相同且互为倒置的V-W多框三角形构形

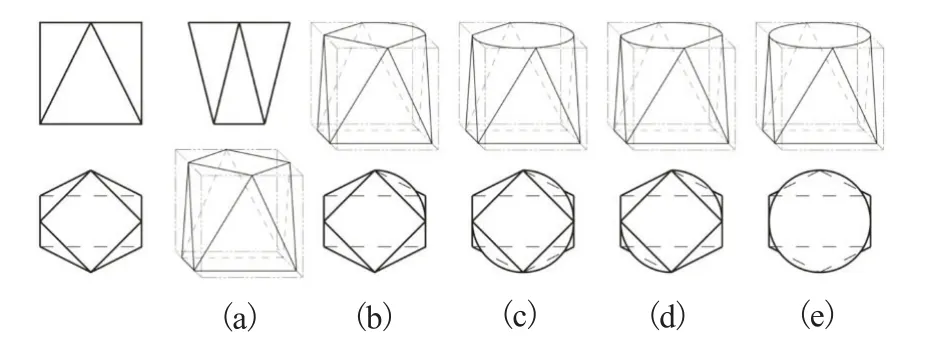
图11 V-W投影中三对三多框三角形对应的部分切割体

图14所示V-W投影中下边线含有一对同面点集，空间对应的最大公共点群域是五边形；W面投影的外轮廓平线e"f"对应V面投影一个点e'（f'），则EF是正垂线，因此含有该正垂线的两个相交平面，对应V面投影中的两个相交斜线均为正垂面，平线为两条铅垂线EE1和FF1的投影重合。对同面点集中的空间几何元素进行排列组合及其形状特征构形，得到如图14（a）～（e）所示的部分形体。

2.3 两面多框含三角形组合的形体构形

图15所示形状相同且互为倒置的V-W投影中，外轮廓的上、下两边线为两对相互平行的同面点集，内部含有两对斜线，构成一对三角形图框和一对五边形图框。对应三角形图框的下边线为一对同面点集，但在可见性相同的条件下不符合投影面垂直面和一般位置面中类似形图框的规律，则该对三角形图框不是同一个斜面的类似形投影，而是两个平行面的投影。当封闭图框代表的是形体上投影面平行面时，该封闭图框亦为不可构表面[12]。对应五边形图框因为含有定线A1E和A1F在内共五条平行线，则该对五边形图框对应空间一般位置面，因此同面点集对应平行面的边线除了不可构直线A1B1和A1D1外，其余边线的形状特征具有可构性的部分形体如图15（a）～（e）。

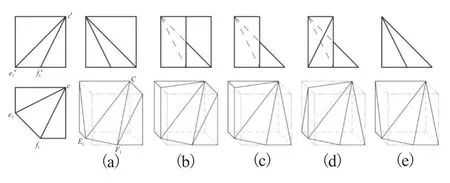
图12 V-H投影中三对三多框三角形对应的部分平面切割体

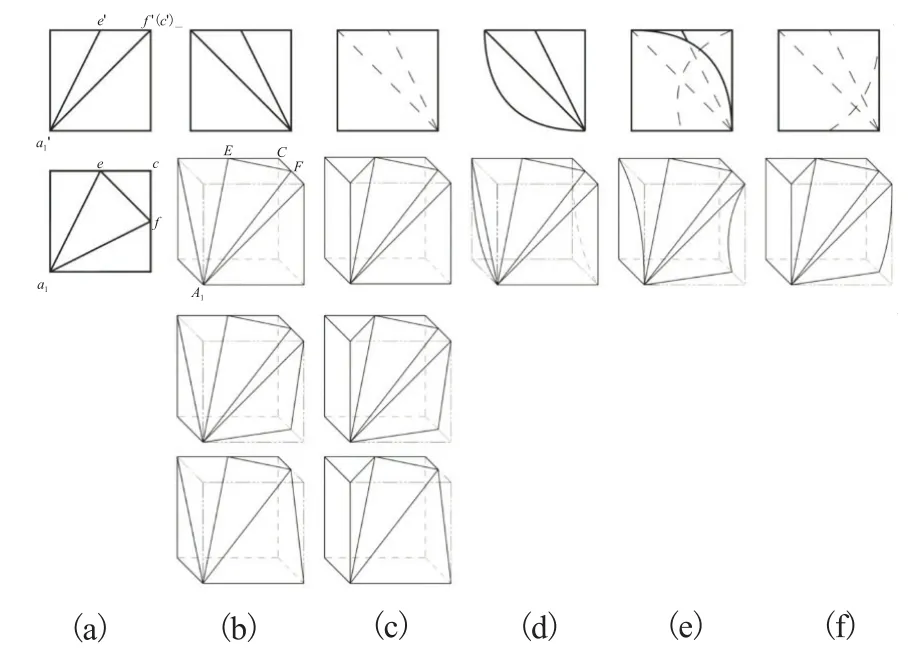
图13 V-H投影中三对四多框三角形对应的部分形体

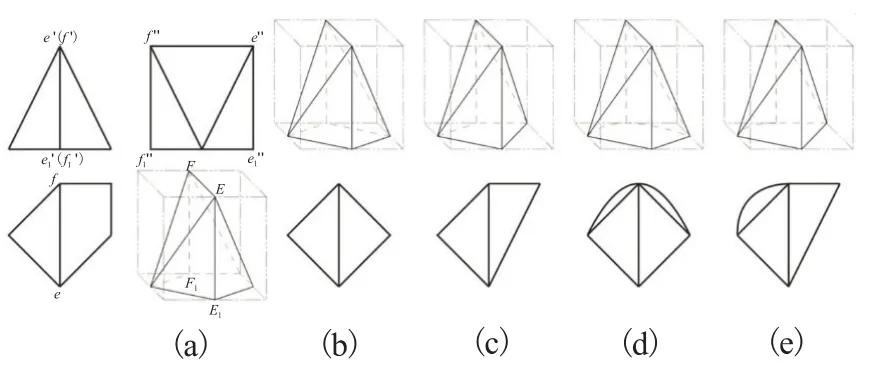
图14 V-H投影中二对三多框三角形对应的部分形体

图16（a）所示形状相同且互为倒置的V-H投影[13]由两对三角形图框和一对菱形图框组成，外轮廓中虽存在一对等长平线但不含有同面点集，该对平线是侧垂线D1C1的投影，待构形的形体表面中含有正平面△ED1C1和水平面△E1D1C1，包含正平线D1E、C1E的△FD1E和△GC1E是正垂面，包含水平线D1E1、C1E1的△FD1E1和△GC1E1是铅垂面，且分别为定形投影；对应菱形图框的四个边分别与定形图框公用，则该对菱形图框为侧垂平面亦为不可构表面。因此满足投影条件的形体具有可逆性如图16（b）。

图17所示V-H多框投影外轮廓为正方形中含有三对子图框，包括两对三角形图框和一对梯形图框。其形体构形应以大带小的方式，即先从图7（a）中确定满足图投影条件的切割体后，再进行具体的细节构形。图7（e）和（f）均符合题设形体构形的原型，在此基础上经过进一步的细节构形，部分平面体如图17（b）～（f）。同样在含有同面点集的平面主体和局部结构中可以构成一系列含有曲面的形体。

图15 形状相同且互为倒置的V-W投影中含有同面点集的多框含三角形组合构形

图18（a）所示V-H投影的外轮廓为正方形，两对相互平行的斜线与同面点集相交，将V面投影分成上（三角形）、中（平行四边形）、下（三角形）三个图框，而H面投影分为后（三角形）、中（平行四边形）、前（三角形）三个图框，按“上对应（组合）后”、“中对应（组合）中”、“下对应（组合）前”的投影方位对应关系，常见平面体如图18（b）～（f），且同面点集具有曲面可构性。

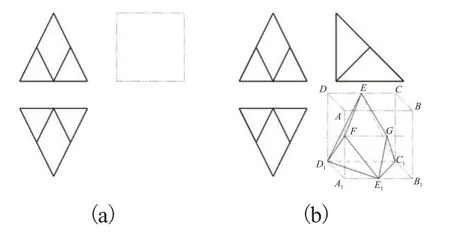
图16 形状相同且互为倒置的V-H投影中不含有同面点集的多框含三角形组合构形

图17 形状、方向均相同的V-H多框含两对三角形组合中以大带小的方式构造出的部分平面体

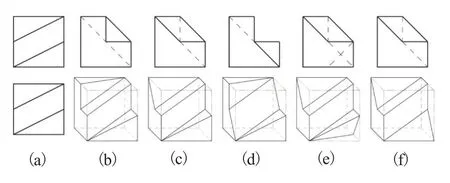
图18 形状、方向均相同的V-H投影中含有同面点集的多框含三角形组合构形

3 小结

在不考虑形体表面的曲率变化以及轮廓线包围区的曲面构形时，含有同面点集的两面单框三角形具有可构性，三角形图框对应椎面的实形、类似形；两面多框三角形组合既与两面单框三角形相关又有独立性，其形体构形一般以切割体为主，根据图框具有的性质及其之间的关联性，可构自由度减少甚至具有可逆性，而可逆性的三角形图框却具有可构性的情况；不含有同面点集的两面投影三角形均为平面体且具有可逆性。将棱柱体、棱锥体作为两面投影三角形的形体构形中的两种分析模型，根据同面点集对应空间几何元素的位置、数目和类属形状进行形体构形设计，对于快速分析图框之间的投影方位对应关系、正确判断图框的可构性与可逆性、构思形体结构形状的多样性与唯一性表达都具有一定指导意义。