基于“相关变化率”的高等数学教学案例研究

（电子科技大学成都学院文理系 四川成都 611731）

在现实的生活中，存在着很多相关变化率问题的案例，要正确地解决这些问题，必须深入地理解相关变化率的含义，掌握相关变化率的实质，从而掌握解题的方法，拓宽学生的知识面。[1]

一、相关变化率的定义

假设有两个可导函数x=x(t)和y=y(t)，变量x与y之间存在某种关系，从而它们的变化率之间也存在某种关系，这两个相互依赖的变化率称为相关变化率。如果已知其中一个变化率要求出另一个变化率这类问题就是相关变化率问题。相关变化率问题广泛应用于我们的生活，下面我们来分析一个生活中的案例。

二、案例引入

在多雨季节，山洪爆发，河流、水库水位上涨迅猛的时候，人民群众的生命和财产安全将会受到极大的威胁，我们都希望在河流、水库的水位到达警戒线之前能够采取有效的措施去避免或减轻险情的发生，因此，水位上升的速度在抗洪预警中具有重大的意义。那么，现在的关键问题是如何计算水位上升的速度呢？[2]

大家都知道，我国小型水库众多，雨季极易发生险情，因此需要对水库的水位情况进行实时监测。下面我们以一个长为400m、顶角为1200的水槽形状的水库为例（如图1），若测得水库上游河水以8m3/s的体流量流入该水库，那么我们要求水深10m的时候，水位每小时上升几米？[3]

图1 水库

如果设水库水流量为V立方米，水深为h米，显然它们是随着时间t变化的，因而这两个变量都是时间t的函数。现在要求水位

三、案例分析

因此，找到变量V和h之间的关系式就是这个问题的关键，而这个关键问题的突破点则是水库的形状。

四、案例求解

设水库水流量为 立方米，水深为h米，显然它们都是时间t的函数。现在我们的关键问题是要寻求V和h之间的关系，这个关系显然隐藏在水库的形状中。

已知水库是长400m、顶角1200的水槽状，我们对水库的形状进行抽象化，就相当于一个平放的三棱柱（如图2）。

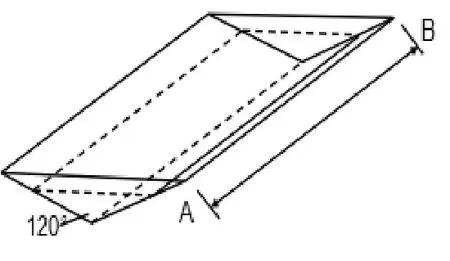
图2

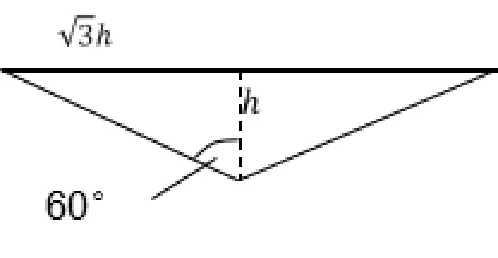
图3

水库的水流量V即为三棱柱的体积V，而三棱柱的体积等于底面积*高。三棱柱的高看作是水库的长AB= 400m。三棱柱的底面是一个顶角为1200的等腰三角形（如图3），这个三角形的高就是水库的水深h，这样，很容易计算出三角形的面积因此，三棱柱的体积将等式两端同时对t求导（注意运用复合函数链式求导法则），得到相关变化率之间的关系，

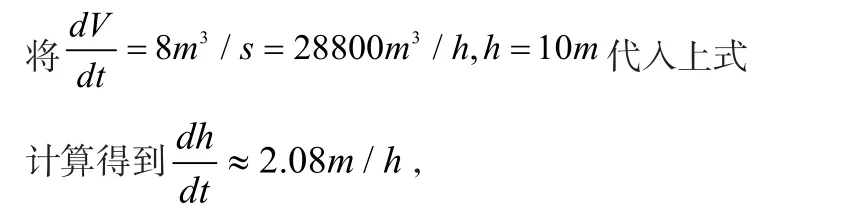
即水深10m的时候，水位每小时大约上升2.08m米。

如果已知水库的警戒线的位置，我们就可以计算出水位到达警戒线所需的时间。这样，在抗洪抢险的时候，抢险人员就可以在有限的时间内采取有效的措施去避免或减轻险情的发生。

五、巩固拓展

问题1：对一圆形的气球充气，气球的体积和半径都随着时间增加，若测得气球体积增加的速度为0.2m3/s，求当气球半径为0.1m的时候，半径增加的速度。

由于气球的体积和半径都是时间的函数，现在已知体积增加的速度，求半径增加的速度，显然这就是一个典型的相关变化率问题，重点就是找到体积和半径的关系。

设气球的体积为Vm3，半径为rm，则V和r都是时间t的函数。

等式两端对t求导，得

即求当气球半径为0.1m的时候，半径每秒大约增加的1.6m。

问题2：

解: 问题中涉及两个关于时间t的函数，s(t)表示等边三角形的面积，h(t)表示等边三角形的高。易知它们之间有关系式

等式两边对t求导，

结语

这几个案例都是我们生活中的相关变化率问题，求解问题的方法、过程都非常相似。通过这两个案例，我们可以总结出求解实际问题的一般步骤：首先，要用数学的语言、数学表达式将实际问题转化为数学问题，寻求数学方法；（2）研究变量之间的函数关系式，建立数学模型；（3）确定计算方法，求解模型；最后，成功解决问题。

求解相关变化率问题，主要是通过复合函数求导的链式法则，利用已知的某变量的变化率得出所要求解的某变量的变化率，其关键是要建立两个变量之间的函数关系式。也可以说，相关变化率问题就是建立简单的数学模型问题。

通过将实际问题转化为用数学知识求解的数学问题，既可以培养学生的学习兴趣，也让学生学会用数学的思维方法分析、解决实际问题。