基于磁流变技术的非球面柔顺数控研抛工具研究

白 冰

（长春职业技术学院 工程技术分院，吉林 长春 130033）

1 引言

非球面元件由于具有矫正像差、改善像质、扩大视场等良好的光学性能而在航空航天、电子、国防等领域得到了广泛的应用[1]。随着科技的飞速发展，市场对非球面的加工精度、加工效率和生产成本都提出了越来越高要求。目前，高精度非球面元件的光整加工依然依赖于传统的手工研抛[2]，生产效率低下，加工质量不稳定，无法满足现代个性化市场的需求。

为了提高非球面零件的加工精度和加工效率，满足市场对高品质非球面零件的需求，各种自动化研抛设备得到了巨大发展，尤其是上世纪八十年代以来，以计算机为主要辅助手段的非球面自动研抛技术得到了快速发展[3-4]。然而，现有的研抛技术中，研抛工具头与非球面之间的研抛力都是通过两者之间的位移变化和接触变形来产生，研抛力、研抛工具的位置和姿态耦合在一起，难以独立、主动、精确控制[5-6]。

磁流变抛光技术（Magnetorheological Finishing，MRF）由文献[7]提出，美国罗彻斯特大学光学制造中心将其用于非球面抛光。该技术利用磁流变效应产生柔性“小磨头”与工件做快速相对运动，从而实现对非球面表面材料的精密去除。该方法易于实现计算机控制，是一种确定性加工技术，能控制加工区域的大小和形状，加工范围广，效率高，可获得高质量光学表面，得到了广大学者广泛关注和快速发展[8-9]。然而，这种以磁流变液作为抛光介质的研抛技术，需要开发专用抛光机床，成本高，大范围推广应用难。

提出一种基于磁流变技术的柔顺数控研抛方法。该方法由一套柔顺研抛工具系统和两轴数控车床构成，研抛过程中的研抛力由工具系统中的磁流变传动装置——磁流变阻尼器（MRD）独立控制，研抛头可绕自身轴线做旋转运动，其伺服进给由两轴数控车床控制，实现了研抛力与研抛工具位移的柔顺控制。基于这一方法，研制了研抛工具系统，进行了实验验证，得到了高质量的非球面表面。

2 工具系统组成及工作原理

2.1 系统组成

开发的工具系统，如图1所示。主要包括：底座、磁流变阻尼器（MRD）、MRD转速输入电机、研抛头转速电机、刀柄、连杆、散热片、可控电流源。其中，底座安装在数控车床的刀架上，MRD转速输入电机刚性固定在底座上，刀柄刚性固定在MRD的外壳上，研抛头转速电机、连杆、研抛头都固定在刀柄上。MRD、可控电流源、刀柄等组成研抛头与非球面之间研抛力控制子系统；研抛头转速电机和连杆构成了研抛头转速控制子系统。

图1 柔顺研抛工具系统Fig.1 Flexible Polishing Tool System

2.2 磁流变阻尼器（MRD）

MRD是一种基于磁流变效应的力矩控制装置，通过该装置来控制研抛头上的研抛力。其结构原理，如图2所示。由外壳、输入轴、磁流变液（MRF）、剪切盘、电磁线圈、散热片等组成。该MRD工作在剪切模式，MFR充斥在剪切盘和壳体组成的容腔内，线圈通电后，可瞬间固化为牛顿流体，当剪切盘在输入电机的控制下转动时，就会在壳体、剪切盘、固化的磁流变液之间产生阻尼力矩T。T由施加在线圈上的电流I控制，I增大，线圈产生的磁场增强，磁流变液的固化程度增大，此时MRD输出的力矩增大，反之，I减小，阻尼力矩也减小。该阻尼器响应快、结构简单、力矩可控性强，可实现对阻尼力矩的无极控制。其力矩输出特性可通过实验测得。

图2 MRD结构原理Fig.2 MRD Structure Principle

2.3 工作原理

该工具系统固定在车床刀架上，如图1所示。伺服进给由数控车床控制，满足加工的刚性要求。对MRD来说，当输入电流一定时，输出力矩是恒定的。研抛过程中，研抛头相对于工件的移动很慢，MRD输出的力矩，通过刀柄、连杆传递到研抛头上，迫使研抛头压紧工件表面，产生了研抛过程中的研抛力。研抛头有两种运动状态，其一是在转速电机的控制下做旋转运动，另一个是在机床数控系统控制下做进给运动，通过路径规划，数控系统可控制研抛头始终以固定的姿态在数控车床的xoz平面内沿着非球面表面进给，实现了研抛头位置的精确控制。在实际研抛中，通过实时控制励磁电流来控制MRD的输出力矩，进而实时控制研抛力。

3 研抛工具系统建模

3.1 研抛力模型

对研抛头与工件表面任一接触点A进行力分析，如图3所示。研抛过程中，研抛头随着研抛工具系统在xoz平面做进给运动，MRD输出的力矩经过刀柄和连杆传递到研抛头上，使得研抛头在研抛点A与非球面表面之间产生了研抛力FA（z，x）。

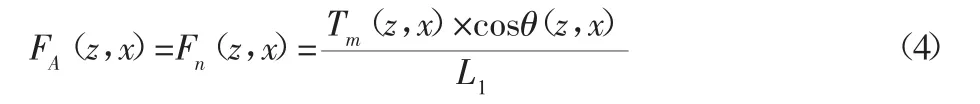
从式（4）可以看出，不同研抛点的研抛力与MRD输出力矩T和θ有关，当MRD输出力矩保持恒定时，研抛力FA（z，x）为：

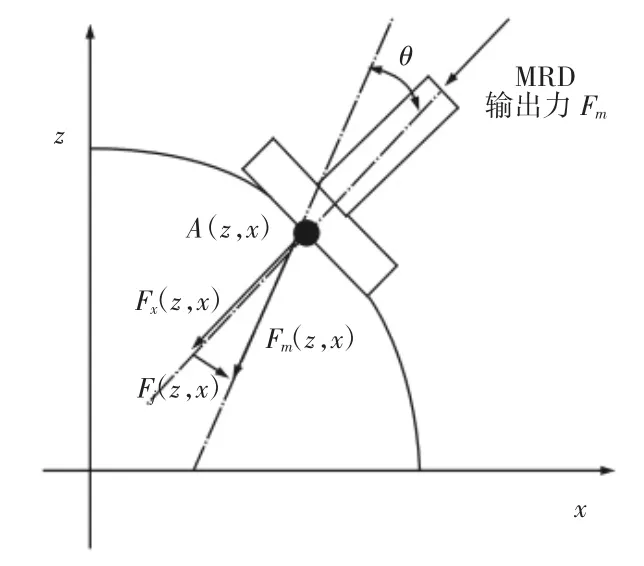
图3 研抛点力分析Fig.3 Polishing Point Force Analysis

假设MRD输出力矩T传递到研抛头上的力Fm（z，x）无损失，在研抛点 A（z，x），Fm（z，x）产生两个分力，一个是沿着非球面法线方向的分力Fn（z，x），另一个是沿着研抛头进给方向上的力Fj（z，x），由图3可知，非球面与研抛头之间的研抛力FA（z，x）就是研抛头对它的法向力Fn（z，x），即：

式中：θ—研抛头连杆与非球面表面法线方向之间的夹角；L1—刀柄长度。

将式（2）和式（3）带入式（1），则可得：

为了获得恒定研抛力，在设计工具系统及规划加工路径的时候，使得连杆方向始终与研抛点法线方向一致，即θ=0，此时，研抛力 FA（z，x）为：

3.2 工具系统动态模型

为了分析研抛力动态传递过程，必须对研抛工具系统其进行动态建模。研抛工具系统框图，如图4所示。PC机的输入信号经过研抛工具系统转换，变为研抛头的研抛力F。F是最终的控制目标，电流Iset是控制变量。其动态系统模型可用下式表示：

式中：G1（s）—电流源和MRD的动态输出函数；

G2（s）—刀柄和连杆的输出函数。

图4 研抛工具系统框图Fig.4 System Diagram of Lapping Tool

3.3 工具系统动态模型辨识

在设计的MRD动态性能测试实验台上，用阶跃响应来辨识包括电流源和MRD的传递函数。实验测试的阶跃响应曲线，如图5所示。根据系统辨识的知识，图5的动态特性可用带有延迟环节的一阶惯性环节来近似，其传递函数具有如下形式：

图5 MRD阶跃测试Fig.5 MRD Step Test

经过辨识，电流源和MRD的动态输出函数G1（s）可表示为：

由于MRD输出的力矩只经过刀柄和连杆的刚性传递，假设力矩传递效率为K，则刀柄和连杆的动态输出函数G2（s）可表示为：

综合式（7）、式（9）、式（10），整个工具系统的传递函数为：

4 工具系统动态仿真

工具系统的动态仿真图，如图6所示。

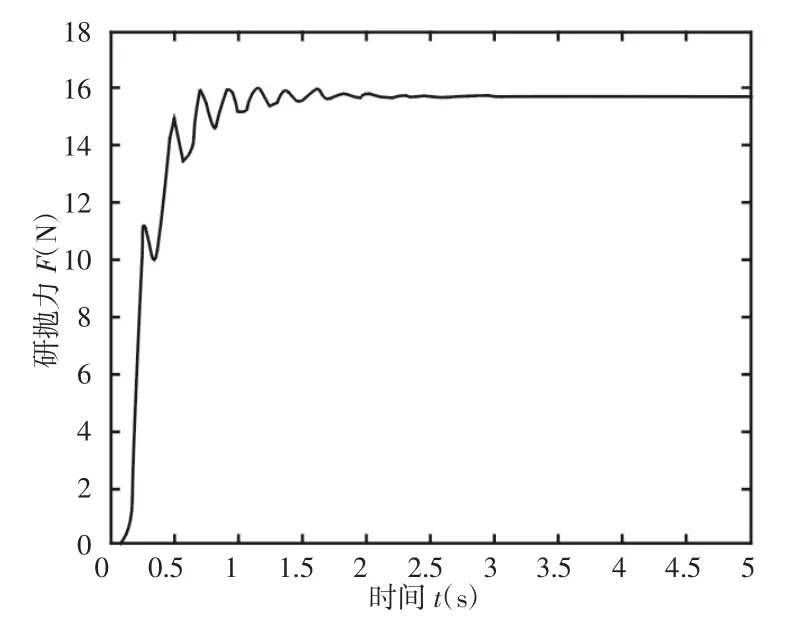
图6 无控制仿真Fig.6 Uncontrolled Simulation

从图6可知，工具系统反应迅速，超调量小，但存在一定延迟，为了确保研抛过程中MRD输出的研抛力精确、迅速，需要设计合适的控制器。采用MATLAB软件进行仿真建模，以单位阶跃信号为输入，采用PID算法，进行Ziegler-Nichols整定，得到的 PID参数为KP=0.9、KI=5、KD=0.01，仿真结果，如图7所示。

图7 PID仿真Fig.7 PID Simulation

5 实验验证

为验证提出方法的有效性，在开发的实验系统上，对工具系统动态性能进行实验验证，并进行研抛实验。

5.1 动态性能验证

在静态下进行测试，工件做旋转运动，研抛头不进给，采用（0.5～1.0）A的阶跃电流作为输入，对研抛头与非球面之间的研抛力进行测量，传感器安装在研抛头与研抛介质之间，响应曲线，如图8所示。可以看出，MRD输出力矩无超调，但达到目标力矩需要的时间长，这与仿真结论是一致的。采用PID控制实验结果，如图9所示。从图9可知，在PID控制下，上升时间为0.1s，调节时间为0.8s，系统具有较好的响应特性。

图8 阶跃响应实验Fig.8 Step Response Experiment

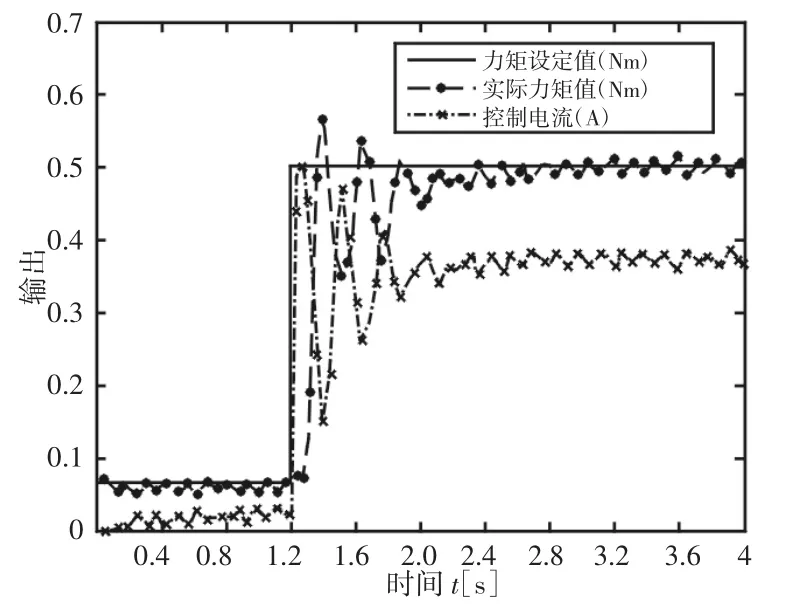
图9 PID控制实验Fig.9 PID Control Experiment

5.2 研抛实验

选用铝制非球面为试件，抛光盘为5mm羊毛毡，磨料为金刚石抛光膏，粒度分别为W2.5，W1.5和W0.5，研抛效果和粗糙度检测结果分别，如图10所示。从图10可以看出，研抛后，非球面的表面质量有很大的提高，表面粗糙度为0.028μm。

图10 非球面研抛结果Fig.10 Aspheric Polishing Results

6 结论

（1）提出了一种基于磁流变技术的非球面柔顺数控研抛技术，开发了相应的研抛工具系统，实现了研抛力的柔顺控制。

（2）建立了研抛力模型和工具系统动态模型，经过辨识，该系统可简化为一个具有延迟环节的一阶系统。

（3）对工具系统动态模型进行了仿真研究，采用常见的PID控制器进行控制，得到了相关参数。

（4）进行了系统动态性能和研抛实验验证，结果表明，系统动态性能与仿真结果相一致，采用PID控制，可实现较好的响应，可获得表面粗糙度Ra=0.028μm的非球面镜面表面。