倍力桥的力学特性分析及其结构优化

许明瀚

（北京 100000）

桥梁是跨越江河湖海、深沟峡谷等障碍的人工构筑物，是交通设施互联互通的关键节点和枢纽工程，在众多种类的桥梁中，倍力桥（Bailey Bridge）是人们利用较多的一种便利桥。虽然现在桥梁技术十分成熟，世界各地都有沟通着山川沟壑的桥梁，甚至是跨海的超级大桥，但是倍力桥依然存在极大的用途，比如科考队员勘察地质、田野实习时的小跨度跨越，地质灾害后抢险救灾时的道路连接等等，因此对倍力桥进行结构优化依然具有实际意义。本文首先对倍力桥的力学特性进行详细的分析，然后基于此对倍力桥结构进行优化，使其能够更加高效地为人们的生产生活服务。

1 倍力桥的力学特性分析

倍力桥模型如图1（a）所示，取其中代表性杆件进行受力分析，整个倍力桥承受的荷载通过中间起连接作用的圆截面横木传递到方形截面杆单元上，我们假设在横木对梁单元支撑的节点上受力均为铅垂方向，以中间节点为例，节点上受向下的作用力N，该梁单元与水平方向的角度为θ，于是N可以分解为垂直于梁单元的力和平行于梁单元的力，由于平行于杆方向的力相对较小，且梁在较小轴向力的作用下抗压性能较好，故可以忽略不计，因此我们重点考虑垂直于杆方向力的影响。

基于上述假设，我们建立了图1（b）所示的三点弯模型，假设简支梁的长度为2L，在梁的中点受向下的力P，通过平衡方程可知，支座反力均为0.5P。由此可以得到三点弯梁模型的剪力图和弯矩图，分别如图1（c）、（d）所示。简支梁的弯矩为：

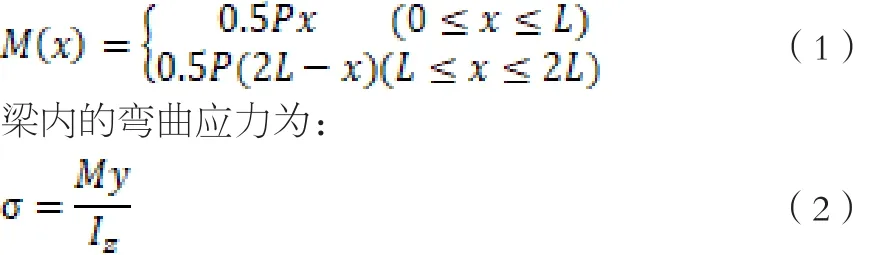
2 倍力桥的结构优化

从第二部分的结果可以看出梁截面高度随位置x满足关系式（4）时，梁所需材料是最节省的，但考虑到实际的生产加工，抛物线形截面加工比较困难，从图2中可以看出，在较小的x范围内抛物线与一次函数之间相差较小，因此可以用一次函数关系近似替代关系式（4），从而达到对倍力桥梁单元的优化效果。

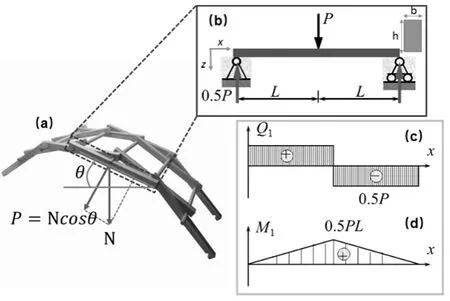
图1 倍力桥的力学建模示意图及其受力分析

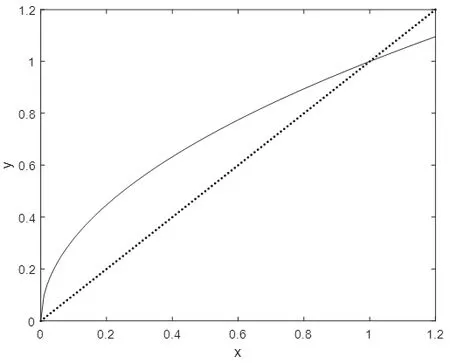
图2 和函数曲线图

由公式（2）可知梁截面的应力随y是线性分布，即梁截面承受弯矩主要是靠近边缘的部分，因此在梁中间部位可以适当的减去部分材料，这样在很小的承重损失下可以极大地减少耗材，也可以极大地减轻倍力桥的自重，综合提高倍力桥的应用性能。如图3所示，假设在截面尺寸为的梁截面中切去尺寸为的长方形，假设，其中k为比例因子，由此可得：

由图3的应力变化曲线可知随着梁质量的减小，截面内的应力逐渐增大，当梁内最大应力达到许用应力时，将会得到最大的截面尺寸因子，此时也将会是最节省材料的截面尺寸临界点。考虑到实际加工的方便可行性，可从横向（垂直于受弯方向与梁长度方向）打孔，这与上述优化理论分析是等效的。综合上述两种优化方案，最终可以得到倍力桥梁单元的优化结果如图3中优化结果所示。再将倍力桥每个梁单元都使用本文所提出的优化模型替换，就能整体提高倍力桥的力学性能。

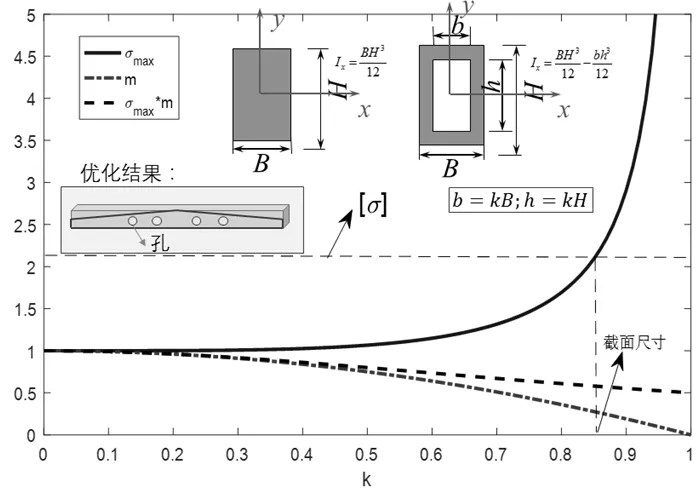
图3 梁单元优化理论分析

3 结语

本文先通过材料力学知识对倍力桥的力学特性进行了分析，即根据倍力桥的受力特点将其简化为三点弯梁模型，得到其剪力图和弯矩图，进而可以求出梁内的最大弯曲应力分布，根据强度条件得到梁截面高度随位置的变化关系，基于此对梁单元进行优化。同时根据梁截面上应力大小的分布特点可以对梁继续进行优化，即在梁上适当地截出一些孔洞，可以在牺牲很小的强度性能下节省更多的材料，同时极大地减轻了梁的自重。综上，通过本文的优化设计可以使倍力桥更加高效地服务于生产生活。