基于绿色施工的铁路填土路堤施工机群配置

郑雨茜，鲍学英



基于绿色施工的铁路填土路堤施工机群配置

郑雨茜，鲍学英

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

基于铁路绿色施工对铁路的可持续发展具有重要作用，为了最优平衡西北寒旱地区铁路工程成本和施工绿色度，针对工程的技术可行性，以铁路填土路堤为研究对象，引入绿色施工成本，建立基于绿色施工下的铁路填土路堤施工机群配置模型。选取具有控制性的16个决策度指标，确定2种配置情况，运用极差最大化组合赋权法对模型中的决策偏好系数进行赋权；基于引入Pareto局部下山算子和差分算子的Memetic免疫优化算法(MIAMO)对模型进行求解，优选出最佳的施工机群配置情况。通过实例研究验证了模型的实用性和算法的可行性。

铁路填土路堤；绿色施工成本；机群配置；极差最大化组合赋权法；Memetic免疫优化算法

国家“十三五”规划把生态建设列入奋斗目标，树立绿色的发展理念。铁路行业作为土木工程领域的行业巨头，常见于在施工阶段产生环境负影响，因而其绿色施工势在必行。铁路绿色施工，即在保证铁路工程质量安全的前提下，利用经过改进后的技术方法和科学管理思想，最终实现铁路建设的低消耗率，减小环境负影响的发生概率[1]。相关文献资料显示，施工机械是铁路施工中产生负面影响最大的因素之一，而且施工机械费的占比约为1/3[2−3]，尤其在西北寒旱地区，施工机械已经很高程度地替代了很多人工作业。因此，科学合理地配置及组织优化施工机群，才能最优平衡绿色施工和经济的关系。绿色施工下的填土路堤施工机群配置，即是在技术可行的条件下尽可能达到“四节一环保”。高效的施工机群配置常有：取土点与填筑点相距50 m以上，挖掘机挖出的土的含水率在最佳含水率附近，在压实之前不需要专门洒水；为了保持原土的含水率，推土机前卸土长度有一个限定值，压路机前推土机推平长度也有一个限定值；同时，各机械互等的可能性最小[4−5]。整个机群进入稳定状态之后，机群的耗能最小(节能)；机械都尽可能运转，减少临时停放(节地)；原土最佳含水率的保持，使得不用再额外洒水压实(节水)；运输损耗相对减小(节材)；机械的扬尘、噪声、振动等得到一定程度地控制(环保)。为此，本文基于铁路填土路堤的机群作业系统，引入绿色施工成本[6]，建立基于绿色施工的填土路堤施工机群配置模型，运用极差最大化法和MIAMO算法进行求解[7−11]，见图1。

图1 填土路堤施工机群优化配置流程

1 铁路填土路堤施工机群系统

铁路填土路堤的机群作业系统一般称作“挖掘—压实”系统，文献[4−5]将其工作过程抽象为5个子系统：AB(挖掘—运土)子系统、BB(卸土—空返)子系统、BC(卸土—推平)子系统、CD1(推平—初压)子系统和D1D2(初压—终压)子系统。见 图2。

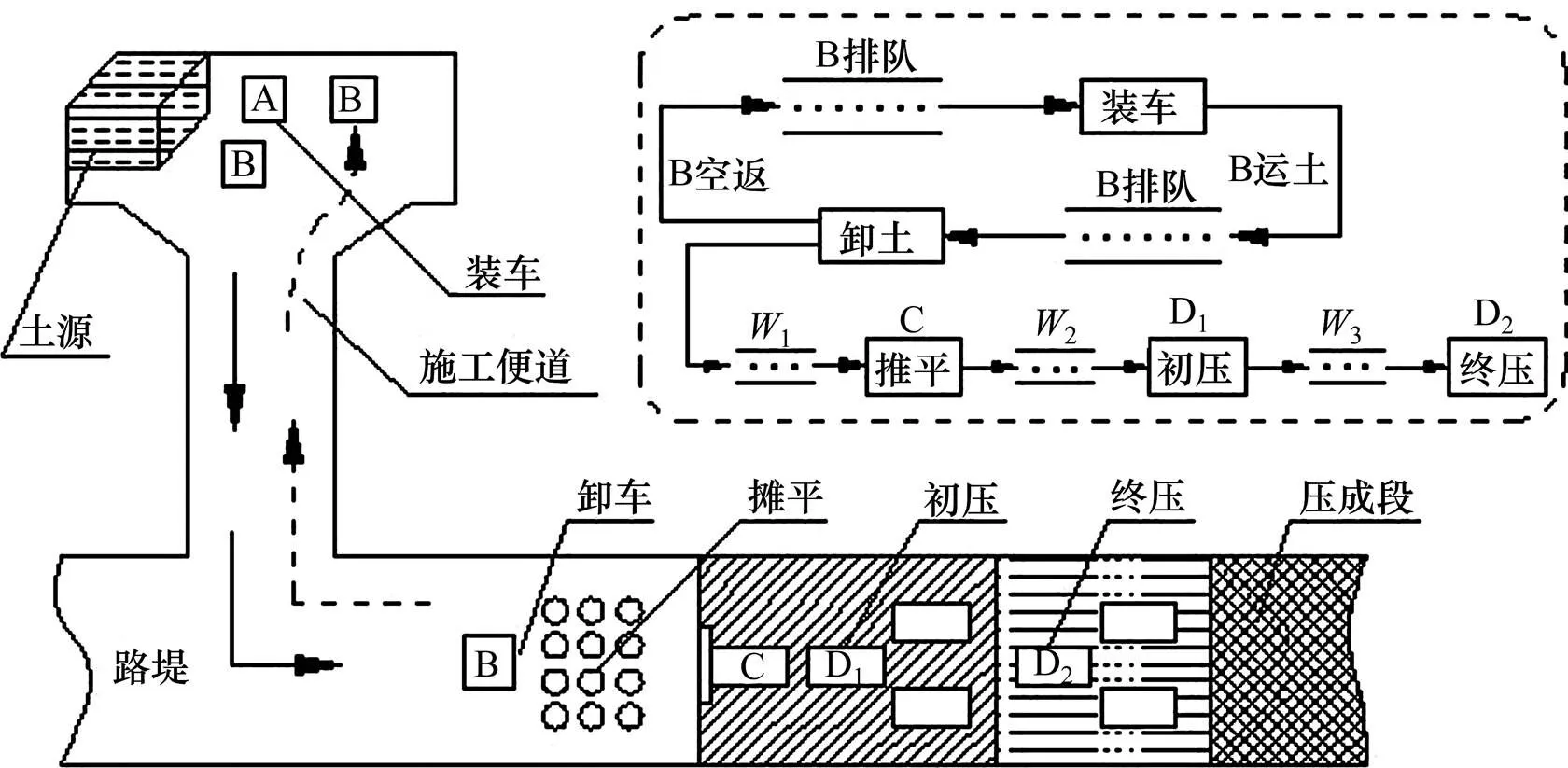
A—挖掘机；B—自卸车；C—推土机；D1—初压压路机；D2—终压压路机； W1—卸土段限制长度；W2—推平段限制长度；W3—初压段限制长度

2 基于绿色施工的机群优化配置模型

2.1 工期—成本—质量的机群配置模型

根据文献[2−3]的研究，已建立了关于工期—成本—质量的多目标函数的填土路堤施工机群优化配置模型(式(1)和式(2))。该模型将工程的工期和成本用一个专门的函数对应关系进行表示；引入质量成本模型对工程质量进行修正[12−13]，即取质量总成本最小值表达式，将产品的购买价格转化为施工机械设备费用，将极限质量保证成本转化为费用最大值(式(1))。

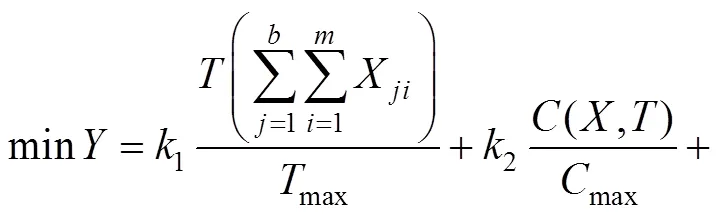
式中：为施工机群配置方案；()为关于机群配置方案的工期函数；()为施工机械设备费用函数；max为机械设备费用函数最大值；min为机械设备费用函数最小值；max为工期函数最大值；X为第个工作面第种机械的工作台数；C为第种机械每台每天的费用；X为第种机械的数量；T为第个工作面的完工时间；U为第种机械的工作班次；P为第种机械的台班工作率；Q为第个工作面的工程量；K为第种机械的总数量；为合同要求工期；1为决策者对工期的偏好系数；2为决策者对成本的偏好系数；3为决策者对质量的偏好系数；为工作面的划分数；为机械的种类数。

此外，在该机群配置模型中，决策变量={∈(1),∈(1,)|x1,x2,x3,…,x,…,x}表示第个工作面所需要的各种施工机械数量所组成的向量，其中：x是整个模型的自变量，表示第项工作所对应的组织方式总第中机械的数量需求。

2.2 基于绿色施工的工期—成本—质量机群配置模型

基于绿色施工的机群配置模型，即在既有的工期—成本—质量机群配置模型的基础上，将绿色施工考虑在内，对土方路堤填筑工程进行施工机群优化配置，以期同时兼顾工程工期、费用、质量和施工绿色度。这里，施工绿色度是一个更加趋于定性的虚的概念，于是，本文引入绿色施工成本的概念进行机群优化配置。

2.2.1 绿色施工成本

绿色施工成本并非传统的施工成本与采取绿色施工措施所耗费的成本简单叠加，因为采取绿色施工措施往往可以达到节材、节地、节水、节能的目的，从而降低施工成本；同时，绿色施工措施的采取还能保护环境，长远来看也是一种成本节约。

参考质量成本的概念，这里给出绿色施工成本的概念表达式，如式(3)~(5)。其中，绿色施工控制成本()是指为了保证满意的绿色度而需要的投入，且与绿色施工水平相关，是早期投入成本；绿色施工损失成本()是指由于没有达到满意的绿色度所造成的损失，是施工结束后才能体现的，是结果成本。同时，参考文献[13]并结合Tayor展开式给出图3的绿色施工损失成本模型(1表示极限绿色施工损失成本)和图4的绿色施工控制成本模型(2表示极限绿色施工控制成本)。

绿色施工成本=绿色施工控制成本+

绿色施工损失成本 (3)

绿色施工控制成本=绿色施工措施投入成本+

预防成本+鉴定成本 (4)

绿色施工损失成本=环境损失成本+

内部损失成本+外部损失成本 (5)

由式(3)及图3~4，参考质量成本指数函数模型，给出绿色施工成本模型：

式中：C(G)为绿色施工成本；a1为极限绿色施工损失成本；a2为极限绿色施工控制成本；b1为追加成本费增长率；b2为控制成本费增长率；G为绿色施工水平。

图4 绿色施工控制成本模型

考虑工程所在地域条件为西北寒旱地区，地质多为湿陷性黄土，生态敏感脆弱等一系列特 点[14−15]。参考文献[6, 12−15]，这里1，2均取0.5，取0.65，无量纲化处理后即得出修正后的绿色施工成本模型表达式(7)(式中字母意义与前文一致)。

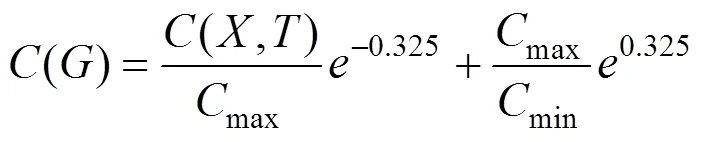
2.2.2 绿色施工下的工期—成本—质量机群配置模型

基于以上模型的建立和探讨，本文建立如式(8)所示的基于绿色施工的工期—成本—质量机群优化配置模型评价函数(约束条件同式(2))：

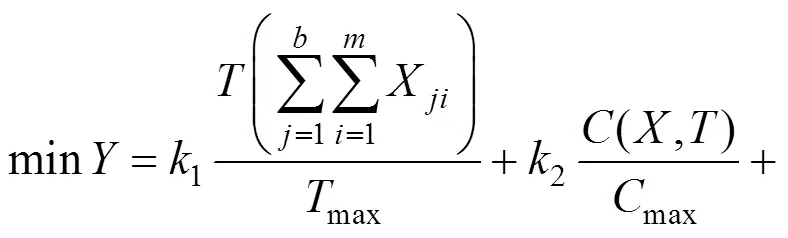
式中：4表示决策者对绿色施工的偏好系数，其余字母意义同前文，且满足：12341(k>0，1, 2, 3, 4)。可以看出，k的取值很大程度决定了何种施工机群配置方案能够使得评价函数值最小，因此，决策偏好系数k的确定对于模型优化来说至关重要。

3 决策偏好系数权重求解

3.1 评价指标的选取

基于前文建立的优化配置模型，结合土方填筑路堤的施工机群作业系统工作过程，参考相关文献给出了以工期、成本、绿色施工、质量为准则层的评价指标体系，详细的评价指标体系见表1。其中，工期、质量准则层指标是为了保证技术可行性，成本和绿色施工准则层指标是经济效应指标。

表1 决策偏好程度评价指标体系

Table 1 Decision Index system of decision preferences

准则层指标层指标测算方法 工期k1自卸车装、卸排队总长度k11参考文献[4] 施工机群暂停工作总概率k12各施工机械暂停工作概率之积，参考文献[5] 一个工作循环内暂停工作时间k13各施工机械暂停工作时间之和，参考文献[4, 5] 一个工作循环纯时间k14各施工机械纯工作时间之和 费用k2机械台班损失费k21参考文献[4, 5] 施工机群联合作业系数k22各施工机械联合作业系数之积，参考文献[4, 5] 机械台班费综合利用率k231− k21/机群一台班总费用 机械群折旧(租赁)费k24施工设备采购资料记录 机械群保养费k25施工资料及施工机械维修保养制度

3.2 极差最大化组合赋权法

3.2.1 4种单一赋权法对指标赋权

采用表2中的4种单一赋权方法进行决策度指标权重的求解。

3.2.2 极差最大化法确定权重向量

1) 求第个评价对象的综合评价得分：

2) 将4种单一赋权法求得的综合评价得分进行组合形成综合得分矩阵，标准化处理得Z，并求得其协方差矩阵：

3) 根据最大差距拉开评价对象的极差差异原则，得到如下线性规划问题：

由文献[7]可知，上述线性规划问题即式(11)的最优解即为所求的单一赋权值调节向量，记为(1,2,3,4)。由此可以得到最终第个指标的组合权重θ：

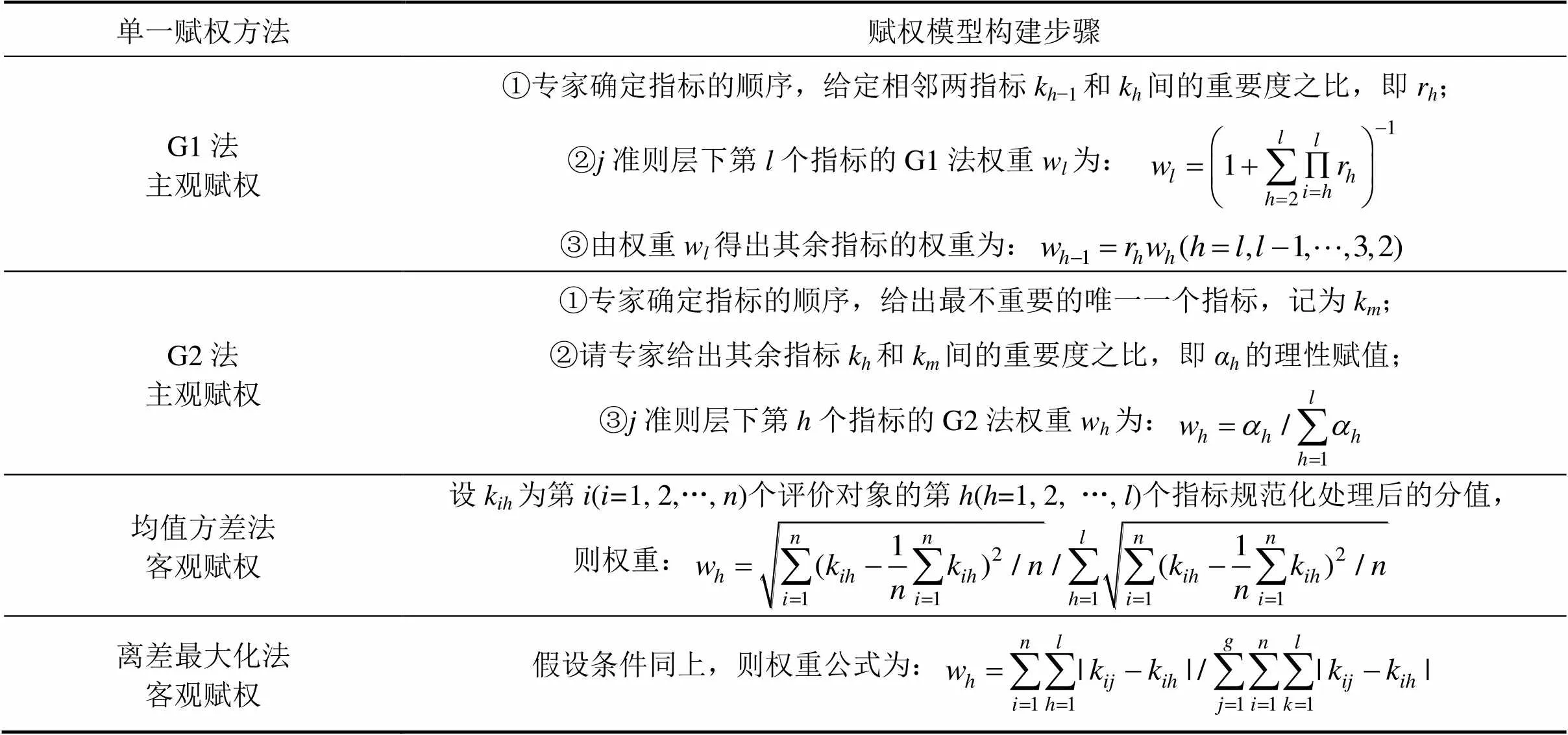
表2 4种单一赋权法步骤

4 模型求解——Memetic免疫优化算法(MIAMO)

Memetic免疫优化算法(MIAMO)，是Memetic算法(MAs)和NNIA2算法(图5)的结合。将MAs中基于Pareto支配关系的局部下山算子和差分算子引入NNIA2算法中，从而进行更快速、更精准地求解。

图5 NNIA2算法迭代模型

4.1 MIAMO算法流程

Step0：算法设置：令激活种群规模n，非支配种群规模n，克隆种群规模n，近邻列表规模，最大函数评价次数；

Step 1：初始化：令初始激活种群0Ø，初始克隆种群0Ø，随机产生规模为n的初始种群0，迭代次数0；

Step 2：克隆操作：采用NNIA2算法，选出规模为n的激活种群A；执行自适应等级克隆操作，得到克隆种群C；

Step 3：免疫基因操作：令C’=Ø，对C中的每个抗体Ab(=1, 2, …,|C|)，用其欧式距离最小的个抗体构成近邻列表(Ab)，再对Ab以概率P执行Step 3.1.(提高算法搜索效率)，以概率1-P执行Step 3.2.；

Step 3.1：Memtic算子：执行基于Pareto支配关系的局部下山和DE的Memetic算子，产生新的抗体：′, ←(Ab,C),′=C′′；

Step 3.2：交叉变异算子：执行模拟二进制交叉算子(SBX)和多项式变异算子(PM)，产生新的抗体：′,′=C′′；

Step 4：选择操作：采用快速非支配排序和基于k近邻的多样性保持技术，从P′中选出n个抗体，构成种群P+1；

Step 5：判断停机准则：若评价次数≥，输出P+1；否则，令+1，转Step 2.。

4.2 基于局部下山和DE的Memetic算子

4.2.1 算法流程

Step 1：计算支配关系：用(Ab)表示(Ab)中被Ab支配的抗体组成的集合，则：(Ab)≠ØStep 2.；(Ab)=ØStep 3.。

Step 2：局部下山算子：记(Ab)={1,2,…,Ab,}，计算下山方向集合={1,2,…,d,}，其中，d =Ab—Ab(1,2,…,)。那么，局部下山算子在抗体Ab的邻域内沿着方向以步长step搜索产生新抗体′：

Step 3：差分算子：随机选择(Ab)中的2个抗体Ab和Ab，则按下式产生新抗体′：

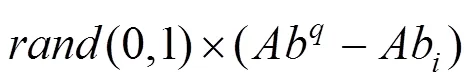
Step 4：返回′。

4.2.2 作用原理和搜索特性

本文根据数值实验模拟分析，探讨基于Pareto的局部下山算子和差分算子的作用原理和搜索特性。分析结果见图6~9。

图6 局部下山算子作用原理

从图6和图7可以看出，局部下山算子会以较大概率获得更接近理想解的子代个体，而且在进化的初期能够有效提高算法的搜索效率，加速算法收敛。

图7 局部下山算子搜索特性

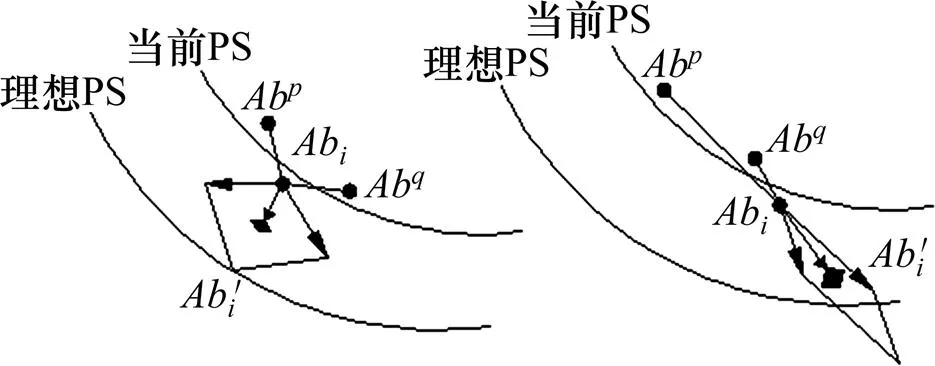
图8 差分算子作用原理

图9 差分算子搜索特性

分析图8和图9，差分算子搜索范围不仅仅局限于当前种群个体围成区域的内部，而且沿着当前PS流形方向朝着两端进行扩展，同时扩展范围渐渐收敛到多目标优化问题的理想PS周围，有助于获得整个理想PS上的解，以提高算法的宽广性和均匀性。

5 实例研究

5.1 项目背景

本文选取兰州至中川机场城际铁路ZCTL— SG4标段的借土填方路堤进行施工机群配置分析。查阅该工程施工单位的施工组织设计获知如下工程概况。

1) 该标段起讫点桩号为：DK40+500~DK63+ 089；

2) 该标段借土填方量为163 162 m3；

3) 填土土源距施工现场5 km；

4) 路基填筑(含附属)工程工期安排为：2013− 07−16~2014−02−28，经折算处理后路基填筑工程工期约为：175日历天，每天工作8 h；

5) 该施工单位拥有的与填土路堤相关的施工机械及规格见表3(台班价格根据地域条件和实际情况经过了折中处理)。

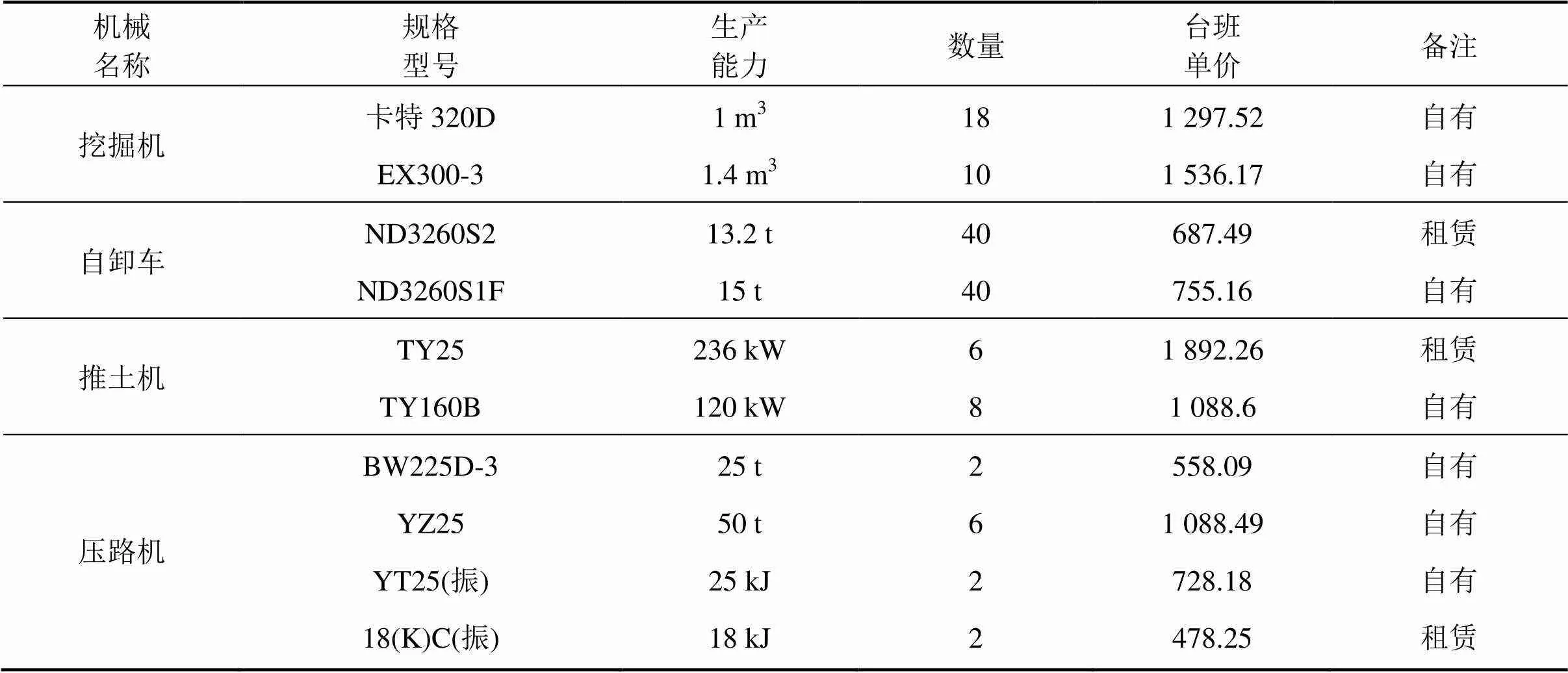
表3 施工机械情况

5.2 决策偏好系数的确定

根据本文第3节内容，对该项目机械配置优化模型中的决策偏好系数进行求解。其中，对线性规划问题即式(11)进行求解即得到在4种单一赋权法下的调节量为=(0.298 7, 0.210 6, 0.233 9, 0.256 8)。其余求解结果见表4。

其中，G1法和G2法是主观赋权，由专家给出相应赋值再进行计算即可。均值方差法和离差法是客观赋权，根据实例项目中的机械情况，该工程的机械配置方案一共有25=32种，具体应该针对每一种配置情况计算出相应的决策度指标，并进行规范化处理，然后根据公式计算权重。

表4 决策偏好系数权重

5.3 机械配置优化模型求解

运用第4节的MIAMO算法对模型进行求解，对于求解结果是非整数的，分别取相邻的2个整数再与其他结果进行组合，计算比较后取最优组合。求解结果见表5。

算法设置为：非支配种群规模n=100，激活种群规模n=20，克隆种群规模n=50，近邻列表规模=20，搜索步长step为当前父代抗体与近邻列表中与其有支配关系抗体之间的平均距离；设置Pareto最优解个数为500，SBX概率为0.8，PM概率为1/4。

表5 机械配置优化模型求解结果

由表5的运行结果可知，本文所建立基于绿色施工的西北寒旱地区铁路填土路堤施工机群配置模型是科学实用的；同时极差最大化组合赋权法和MIAMO算法对模型也起到了很好的优化目的，这为后续的研究工作奠定了基础。

6 结论

1) 引入绿色施工成本的概念，在前人研究的基础上建立基于绿色施工的机群配置模型，基于工程技术可行性，最大程度优化绿色施工和成本之间的关系。这对于铁路行业的施工机群配置有一定的指导作用，同时对铁路的绿色施工有着启发性的 意义。

2) 选取有控制性作用的决策度指标，基于极差最大化组合法对模型决策偏好度进行求解，这为企业决策者提供了一种决策新思路。同时，2种主客观的单一赋权法对指标权重进行求解，既有效克服了主观因素的决策失误，也避免了数据偏差而产生的评判错误，并保证了评价结果的科学性。

3) 运用MIAMO算法对多目标优化模型进行求解，引入基于Pareto支配关系的局部下山算子和差分算子，使算法避免陷入局部最优，保持种群的多样性，保证解空间的良好逼近性、均匀性和宽广性，还提高了算法的搜索效率，加速算法收敛。这对于多目标优化模型的求解有一定的参考价值。

4) 铁路施工的绿色度是一个错综复杂的庞大体系，本文选取的基于施工机群配置的绿色度决策偏好指标可能不够全面，应当进一步对绿色施工影响因素进行研究优化，以期更加完善的模型。

[1] 孔繁玉. 绿色施工理念下铁路工程施工安全风险预警[J]. 山西建筑, 2016, 42(11): 248−250. KONG Fanyu. Railway construction safety risk warning under green construction concept[J]. Shanxi Building, 2016, 42(11): 248−250.

[2] 晁玉增. 基于粒子群算法的公路施工机群优化配置研究[D]. 南京: 南京林业大学, 2011. CHAO Yuzeng. Research on optimized collocation of highway construction cluster based on particle swarm optimization[D]. Nanjing: Nanjing Forestry University, 2011.

[3] 刘欢. 公(铁)路土石方施工机群配置仿真方法的研究[D]. 长沙: 中南大学, 2014. LIU Huan. Research on the method of collocation simulation for earthwork construction in gonglu (iron) road[D]. Changsha: Central South University, 2014.

[4] 郭小宏. 如何合理确定“挖掘—运输”系统的机械配比[J]. 筑路机械与施工机械化, 1986(4): 22−29, 41. GUO Xiaohong. How to reasonably determine the mechanical ratio of “excavation-transportation” system[J]. Road Construction Machinery and Construction Mechanization, 1986(4): 22−29, 41.

[5] 郭小宏. 一类路堤填方施工中机械运行状态的概率分析[J]. 重庆交通大学学报(自然科学版), 1992, 11(4): 66−75. GUO Xiaohong. Probability analysis of mechanical operating state in embankment filling[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 1992, 11(4): 66−75.

[6] 裴景希. 高层建筑绿色施工成本分析与控制方法研究[D]. 南昌: 华东交通大学, 2016. PEI Jingxi. Study on cost analysis and control methods of high-rise building green construction[D]. Nanchang: East China Jiaotong University, 2016.

[7] 郭亚军. 综合评价理论、方法与应用[M]. 北京: 科学出版社, 2002: 44−51. GUO Yajun. Comprehensive evaluation theory, methods and applications[M]. Beijing: Science Press, 2002: 44−51.

[8] 肖新平, 李福琴, 涂金忠. 基于离差最大化的灰色关联分析法在公路网综合评价中的应用[J]. 公路, 2006(8): 122−126. XIAO Xinping, LI Fuqin, TU Jinzhong. Application of gray relational analysis based on maximizing deviation in comprehensive evaluation of highway network[J]. Highway, 2006(8): 122−126.

[9] Deb K. Multi-objective optimization using evolutionary algorithms[M]. New York: Wiley, 2001.

[10] 焦李成, 杜海峰, 刘芳, 等. 免疫优化计算、学习与识别[M]. 北京: 科学出版社, 2006. JIAO Licheng, DU Haifeng, LIU Fang, et al. Immune optimization calculation, learning and recognition[M]. Beijing: Science Press, 2006.

[11] Hart W E, Krasnogor N, Smith J E. Recent advances in memetic algorithms[M]. Berlin: Springer-Verlag, 2005.

[12] 刘卫东, 应婧. 基于产品寿命周期的质量成本模型及其分析[J]. 管理评论, 2011, 23(2): 117−121. LIU Weidong, YING Jing. Quality cost model based on product life cycle and its analysis[J]. Management Comments, 2011, 23(2): 117−121.

[13] 白宝光, 张世英. 质量成本模型及其优化[J]. 科学管理研究, 2005, 23(3): 29−31. BAI Baoguang, ZHANG Shiying. Quality cost model and its optimization[J]. Scientific Management Research, 2005, 23(3): 29−31.

[14] 张俊, 常涛, 甄海东. 对西北地区建筑工程绿色施工措施的若干建议[J]. 山西建筑, 2017, 43(7): 207−209. ZHANG Jun, CHANG Tao, ZHEN Haidong. Suggestions on green construction measures of northwest construction engineering[J]. Shanxi Building, 2017, 43(7): 207−209.

[15] 冯勇, 侍克斌. 西北地区发展绿色建筑和绿色施工的研究[J]. 建筑技术开发, 2004, 31(8): 82−84. FENG Yong, SHI Kebin. Research on developing green building and green construction in northwest region[J]. Construction Technology Development, 2004, 31(8): 82−84.

(编辑 蒋学东)

Construction machinery cluster configuration of railway filled embankment based on green construction

ZHENG Yuxi, BAO Xueying

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Railway green construction and railway construction are synchronized advance, which are crucial to the sustainable development of railway. In order to optimally balance the cost of railway project and the green degree of construction in the northwest cold arid region, based on the technical feasibility of the project, taking the railway filled embankment as the research object and introducing green construction cost, a construction machinery cluster configuration model of railway filled embankment under the green construction was established. Selecting 16 decision-making indexes with controllability, determining 2kinds of configuration, and the maximal portfolio weighting method was used to weight the decision preference coefficient in the model. Then based on the Memetic immune optimization algorithm (MIAMO), which introduced Pareto local down-hill operator and differential operator, the model was solved and the best configuration of the construction cluster was selected. Finally, by a case study, the practicality of the model and the feasibility of the algorithm were verified.

railway filled embankment; green construction cost; machinery cluster configuration; maximal portfolio weighting method; Memetic immune optimization algorithm

10.19713/j.cnki.43−1423/u.2018.12.029

U215.6

A

1672 − 7029(2018)12 − 3239− 09

2014−11−18

国家自然科学基金资助项目(51768034)；长江学者和创新团队发展计划资助项目(RT1139)

鲍学英(1974−)，女，宁夏中卫人，教授，博士，从事建设项目管理及经济评价；E−mail：813257032@qq.com