基于单个宽带回波提取目标距离和速度的方法

刘明敬，陈建平

(1.南京电子技术研究所，南京 210039； 2.中兴通讯南京研究所，南京 210013)

0 引言

作为反导系统的重要组成部分，宽带雷达发射宽带信号可获取丰富的目标信息，受到科研人员的极大重视。线性调频(LFM)信号是宽带信号中应用最广的一种，对其进行匹配滤波是常见的脉冲压缩处理方式。然而，对于带宽高达1 GHz及以上的系统而言，匹配滤波意味着超高的数据率，这对宽带接收系统和处理系统的硬件要求很高。为降低硬件负荷，通常对回波进行去斜处理，这可大大减少数据量，代价是成像距离会因此缩短。在传统宽带系统中，为提供处理所需的参考时延，通常采用宽窄交替的工作方式，即窄带用于跟踪目标，宽带用于对目标成像。该方式使等效宽带PRF降低一半，且未能充分利用宽带提供的信息。为了充分利用宽带回波提供的信息，文献[1]利用目标速度引起的多普勒频移导致中心频率左右两个匹配滤波器输出幅度的差别实现基于单个线性调频信号的测速，该方法对信号参数和信噪比要求非常严格；文献[2]利用高速运动目标在LFM脉冲串内产生越距离单元走动的事实，基于Keystone变换在校正目标走动的同时实现高精度测速，但该方法要利用多个脉冲且需解决速度模糊的问题；文献[3]研究了对雷达回波信号相位进行最小二乘参数估计实现精确测速的方法，该方法受信噪比影响较大；文献[4]研究了利用多个宽带回波的幅度和相位信息测量目标距离和速度的方法，可减少测距测速的随机误差。

本文研究利用单个宽带去斜回波信号对目标进行同时测距和测速的方法。在分析运动目标宽带去斜回波信号特点的基础上，提出一种基于分数阶傅里叶变换(FRFT)的LFM信号参数估计方法，实现从单个宽带去斜回波信号对运动目标同时精确测距测速。

1 线性调频信号去斜处理方法

线性调频信号去斜脉压处理原理[5]如图1所示。

图1 去斜脉压处理原理图Fig.1 Dechirp processing theory

图中：SR(t)为目标回波信号；SL(t)为去斜本振信号；Sf(t)为混频器输出的中频信号；SN(n)为A/D变换后的中频信号；S(L)为SN(n)经FFT变换后的信号。设发射LFM信号，则宽带回波信号SR(t)可表示为

(1)

式中：rect(t)为矩形包络；f0为起始频率；T为时宽；k为调频斜率；tr为回波时延；SL(t)为参考延时信号。当距离跟踪参考延时为τ0时，混频后的输出Sf(t)为

(2)

由式(2)可见，去斜混频器输出的频率和目标与参考信号间的时延差tr-τ0成比例，与调频斜率有关，而与发射信号起始频率无关。对式(2)进行FFT变换，即可获得目标的一维像S(L)，一维像中各谱峰点代表各散射点的相对距离。

2 运动目标宽带去斜回波特点

R(t′)=R0-vrt′

(3)

往返R(t′)距离所需的时间为

(4)

由式(3)、式(4)可解得

(5)

将tr代入式(1)，整理可得

(6)

设混频参考时延为τ0，则混频后的输出信号为

(7)

令调频斜率ka、中心频率fa、初始相位φa分别为

(8)

(9)

(10)

则式(7)可写作

(11)

由式(11)可知，去斜后的运动目标宽带回波不是单频信号，而是一个LFM信号，其调频斜率与目标的速度vr及发射信号的调频斜率k有关，其中心频率则与参考时延τ0、目标距离R0、目标速度vr、调频斜率k等因素有关。

3 基于单个宽带回波估计目标距离与速度的方法

3.1 算法原理

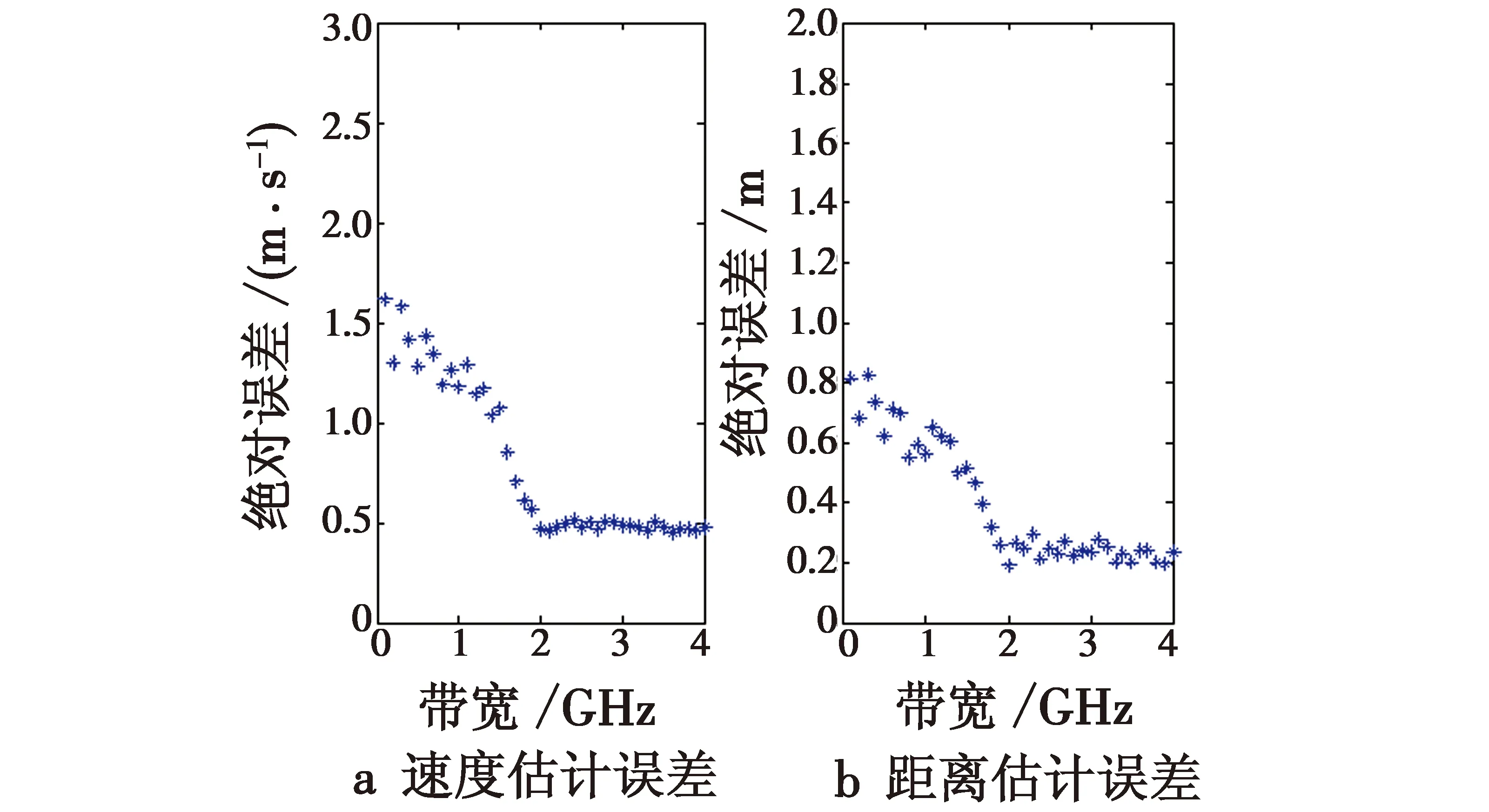
由于运动目标去斜宽带回波是一个LFM信号，估计出其调频斜率ka和中心频率fa，由式(8)～式(10)可计算出目标速度vr及目标与雷达之间的距离R0。由于vr<

(12)

(13)

实现LFM信号检测与参数估计的方法较多，如Radon-Wigner变换和Radon-Ambiguity变换等。本文采用基于FRFT的方法对LFM信号进行检测和参数估计，用较小的计算量即可得到目标速度和距离的高精度估计。

3.2 基于FRFT的目标距离与速度估计算法

信号x(t)的FRFT定义[6-7]为

(14)

式中：p为FRFT的阶，可为任意实数；α=pπ/2；Fp[·] 为FRFT的算子符号；Kα(t,u)为FRFT的变换核，定义为

(15)

FRFT逆变换定义为

(16)

由于运动目标去斜宽带回波为LFM信号，估计目标速度和距离，相当于估计LFM信号的调频斜率和中心频率。因此，利用FRFT实现运动目标的速度和距离估计，实际上是利用FRFT对噪声背景下的LFM信号进行参数估计。

假设某运动散射点目标的宽带去斜回波可表示为含噪单分量LFM信号，即

x(t)=s(t)+w(t)=a0exp[j(φ0+2πf0t+πμ0t2)]+w(t)
-Δt/2≤t≤Δt/2

(17)

式中：a0,φ0,f0和μ0分别表示LFM信号的幅度、初始相位、中心频率和线性调频斜率，均为未知参数；w(t)为零均值加性高斯白噪声。

由于LFM信号在不同分数阶域上呈现出不同的能量聚集性，以旋转角α为变量，对回波序列连续进行分数阶傅里叶变换，形成信号能量在参数(α,u)平面上的二维分布，在此平面上按阈值进行峰值点的二维搜索，即可实现信号的检测和参数估计。对于式(17)给出的信号模型，这一过程可描述为

(18)

(19)

显然，式(18)是一个二维搜索。由于FRFT的计算可借助FFT实现，使得以旋转角α为变量进行FRFT的计算量大大减小。与基于WVD或Radon-WVD的信号检测与参数估计方法相比，FRFT方法省略了Radon-WVD方法中将时频分布从直角坐标到极坐标的变换和二维Radon变换，降低了处理的复杂度；作为一种线性变换，FRFT在分析多分量信号时避免了交叉项的困扰，保留了信号的相位信息，因此可同时估计出多个LFM信号分量的调频斜率、中心频率、幅度和初始相位等参数[7]。当波束内包含多个目标时，宽带去斜回波为多分量LFM信号，利用FRFT及逐次消去法可在分数阶域上进行多分量LFM信号参数估计[7]，实现对多个目标同时测距测速。设旋转角α扫描点数为m，信号样本长度为N(通常数百甚至上千)，采用文献[8]提出的分解型快速算法，本文提出的参数估计算法的计算复杂度为O(mNlgN)，扫描点数m由扫描分辨率和范围来确定，可根据实际应用背景适当选取。在本文利用宽带去斜回波估计目标速度与距离的应用中，进行宽带测量之前，系统已对目标实现了稳定跟踪，可提供较为精确的初始速度，根据式(8)可得到调频斜率的初步估计值和扫描区间，因此可大大缩小扫描范围。显然，与其他基于双线性时频分布的算法(计算量一般为O(N2))相比，本文算法的计算复杂度要小得多。

采用式(18)、式(19)估计得到LFM信号的调频斜率和中心频率后，代入式(12)、式(13)即可得到目标速度和距离的估计。

4 算法仿真与性能分析

采用FRFT对单个散射点运动目标宽带去斜回波提取目标距离和速度进行仿真分析，仿真参数设置为：载频10 GHz，带宽1 GHz，时宽100 μs，采样率10 MHz，参考距离150 m，目标距离162 m，目标速度5896 m/s，回波幅度4。

采用这些参数生成运动目标宽带去斜回波信号，并按不同信噪比添加高斯白噪声，对含噪信号采用FRFT估计目标速度、距离和回波幅度，得到不同信噪比下100次蒙特卡罗仿真结果，如表1所示。其中，当SNR为10 dB时，在100次蒙特卡罗仿真中，速度和距离有较大估计误差的仅有1次，其余99次估计精度均与SNR为12 dB以上的情况相同。仿真结果表明，该算法在SNR不低于10 dB时，可得到目标速度、距离和幅度的可靠估计，三者的估计精度分别优于1 m/s，0.5 m以及3%。更为可贵的是，当SNR下降到-5 dB时，仍可得到较为准确的估计，这充分说明该算法具有相当的稳健性。

表1 不同信噪比条件下的参数估计精度统计

其余参数保持不变，信噪比为15 dB条件下，信号带宽从100 MHz开始，以100 MHz的增量递增到4 GHz，得到的速度和距离估计误差曲线如图2所示。

图2 信号带宽对参数估计精度的影响Fig.2 Parameter estimation accuracy curves under different bandwidths

由图2可以看出，随着信号带宽的增加，估计精度也进一步提高，当信号带宽增加到2 GHz以上时，估计精度基本稳定，但即使信号带宽仅100 MHz，依然可得到较好的估计精度。

其余参数保持不变，信噪比为15 dB条件下，信号脉宽从10 μs开始，以10 μs的增量递增到4 ms，在该范围内得到的速度估计和距离估计精度与表1无明显差异。可见，本文提出的算法可适用于不同信号时宽和带宽。

5 结论

本文深入分析了运动目标宽带去斜回波的特点，得出其为LFM信号的结论，推导了LFM信号调频斜率和中心频率等参数与目标距离和速度之间的关系。在此基础上，提出了一种基于FRFT的LFM信号参数估计方法，利用单个宽带去斜回波信号估计目标的距离和速度。FRFT作为一种线性变换，当去斜宽带信号含有多个目标回波时，可采用逐次消去法在分数阶域上进行多分量LFM信号参数估计，基于单个回波实现多目标同时测距测速。仿真分析和计算结果表明，该算法可用较小的运算量获得目标距离与速度的高精度估计，适合进行实时处理，且广泛适用于不同信号时宽、带宽及信噪比的情况，具有良好的普适性和稳健性，有很好的工程价值和应用前景。