四旋翼无人机飞行控制算法综述
王 成,杨 杰,姚 辉,席建祥
(火箭军工程大学,西安 710025)
0 引言
四旋翼无人机通常采用手持遥控器的方法控制飞行动作,或者通过地面站发送指令控制无人机飞行航迹。在控制指令下,四旋翼无人机可进行垂直起降,并具有多种飞行方式,如悬停、横向飞行以及前后飞行等。四旋翼无人机具有很强的实用性,可以用很小的代价完成各项任务,如近地军事侦察、影视拍摄、农情监测甚至快递业务等[1-3]。虽然目前四旋翼无人机在市场上应用已经相当普遍,但是在技术方面实现其稳定飞行并非易事。国内外学者对四旋翼的飞行控制算法进行了大量研究,提出了诸多控制策略,然而在实际算法设计中,仍存在如下两个方面的难题[4-5]。
1) 难以建立精确的数学模型。就结构而言,4个电机存在安装误差,并不能做到完全垂直于4轴所在的机身平面,且高速旋转时存在振动;此外,4轴也无法做到完全对称,轴臂长度、质量分布并不完全一致[6]。就飞行时空间受力情况而言,四旋翼无人机不仅受到重力、旋翼高速旋转时产生的升力,还要受到气流变化等外部干扰因素的影响[7-8]。
2) 四旋翼无人机是一个典型的多输入输出、非线性、强耦合的欠驱动系统[9]。四旋翼无人机在空间飞行时有6个自由度(沿空间直角坐标系3个方向的位移运动和绕坐标系3轴的旋转运动),但仅有4个可控变量输入(4个电机的转速)。可控变量对无人机的位姿控制存在耦合,且易受到干扰影响,这也使四旋翼的控制变得更为困难。
针对以上问题,国内外学者或简化模型,忽略不确定因素的影响,实现四旋翼无人机基本的飞行控制,如经典PID算法和最优LQR算法;或对非线性、鲁棒性以及综合型算法展开研究,提高控制系统的抗干扰性能和环境适应能力,如反步法、滑模控制、自适应控制等。但无论采用何种控制方法,设计算法之前均是从四旋翼无人机在空间中的转动和平动两种运动状态出发进行系统建模。为全面了解四旋翼无人机飞行控制算法的研究进展,本文研究了近年来关于四旋翼无人机飞行控制算法的相关文献,并进行综述。
1 四旋翼无人机的基本模型
四旋翼无人机在空间飞行时,可以以其机身建立机体坐标系B和地理坐标系E,如图1所示。

图1 四旋翼无人机机体坐标系和地理坐标系Fig.1 The body coordinate system and the geographic coordinate system of the UAV
机体坐标系原点与机身几何中心重合,按照右手定则,三坐标轴{xb,yb,zb}的正方向可设为机身的前、左、上3个方向,如图1a所示。而为了标记机体在空间中的位置,可依托地球表平面建立地理坐标系E,其坐标轴{xe,ye,ze}的正方向可分别记为北、东、上,如图1b所示。电机编号绕zb轴逆时针旋转依次记为1,2,3,4。电机1,3和电机2,4转向相反,控制4个电机的转速即可控制四旋翼无人机的俯仰、横滚和偏航运动。
记ξ=(ξx,ξy,ξz)T为质心在地理坐标系中的位置,η=(φ,θ,ψ)T为机体相对于地理坐标系三轴偏转的欧拉角,即偏航角、俯仰角和横滚角。
推导四旋翼无人机的运动方程可以从牛顿力学出发,如文献[10];也可以从欧拉-拉格朗日方程,即能量守恒的角度出发,如文献[11-12],最终建立平动方程和转动方程。如果均在地理坐标系建模,那么,最终的运动方程可以表示为[12]
(1)
式中:m为机体质量;ax,ay,az是机体在地理坐标系下沿3个坐标轴方向的加速度;u1是四旋翼总升力;dx,dy,dz是分解到3个坐标轴方向的干扰力;Ck=cosk,


2 四旋翼无人机飞行控制算法
四旋翼无人机飞行控制算法在控制结构上可分为内外环,其中,内环为姿态环,外环为位置环,如图2所示。
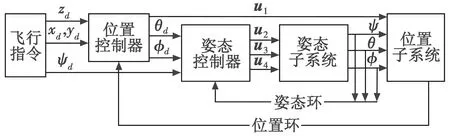
图2 四旋翼无人机控制系统基本结构Fig.2 Basic structure of the quadrotor UAV control system
从式(1)可看出,当旋翼总升力u1一定时,位移加速度就依赖于姿态角的大小,即姿态角可决定飞行航迹。因此,控制系统的一般设计思路为:飞行指令给出期望的位置坐标,位置控制器输出期望姿态角,姿态控制器输出对电机的控制信号。有些不考虑位置控制的四旋翼也可用遥控器的控制指令作为期望的姿态角输入。对于反馈信号位置坐标(ξx,ξy,ξz)和姿态角(ψ,θ,φ)的大小可以由GPS和惯性传感器测出。
四旋翼无人机发展至今,主要的飞行控制算法有经典PID控制算法、LQR控制算法、滑模控制算法、反步法、鲁棒控制算法以及其他控制算法,下面分别进行介绍。
2.1 经典PID控制
目前,市场上大多数四旋翼无人机的飞控算法均为PID控制算法,其具有原理简单、控制技术成熟、易于实现等优点。
PID算法将式(1)线性化为
(2)
对于外环位置控制,设计控制算法为
(3)
高度控制可由uz完成,对于水平方向的控制,ux和uy分别对应式(2)平动方程中的θ和φ,也就是内环姿态控制中的期望角θd和φd。
内环姿态PID控制器设计为
(4)
从式(3)和式(4)可以看出,内外环位姿PID控制器共需18个参数,参数众多,选定合适的参数较为困难。文献[14]从频域的角度出发,探讨了姿态控制器如何选取合适的PID参数,以达到最优的PID控制效果。文献[15]则将PID参数视为变量,设计了模糊控制器,针对不同的飞行状态来选择合适的PID参数值。
目前,PID控制算法已经成功应用于四旋翼无人机的悬停、定高以及航迹控制。PID控制算法的应用比较成熟,但系统鲁棒性能却不够理想,受干扰影响较大。比如在悬停状态下,用风扇模拟风力加以干扰,四旋翼无人机便很难保持稳定。
2.2 LQR控制
LQR即线性二次型调节器,可得到状态线性反馈的最优控制规律,易构成闭环最优控制,基本思想是在满足性能函数取得最优值的约束下,根据相应的原理设计控制器。
LQR控制算法先将四旋翼无人机系统模型线性化,如式(2),并转化为状态方程的形式,即

(5)
式中:x为位姿状态变量;A,B为模型参数矩阵;K为待求反馈矩阵;r为期望状态;u为式(2)中的系统控制量{u1,u2,u3,u4}。
根据式(5)构建全状态反馈控制系统如图3所示,图3中待控制的状态量x分两组,第一组为水平方向的位移和位移速度以及绕x,y轴旋转的姿态角和姿态角速度,主要考虑到它们之间存在内外环的耦合关系(从图2及式(2)中可以看出),故放在一起;第二组状态量为高度和高度方向的速度以及绕z轴旋转的姿态角和姿态角速度,这两个量不与其他状态量耦合,因此可以单独控制。

图3 全状态反馈系统框图
Fig.3 Block diagram of full-state feedback control system
图中,r表示参考输入,x表示系统输出。
系统模型参数确定后,系数矩阵A,B均可确定。为了达到期望状态,关键在于配置反馈矩阵K,使闭环系统的极点处于复平面左边合适的位置,从而使状态稳定到期望值。K的取值与Riccati方程有关,即
ATP+PA+Q-PBR-1BTP=0
(6)
式中,P,Q,R均为矩阵。该方程具体推导过程可参考文献[16]。
反馈矩阵K可通过以下3步计算:1) 选择参数矩阵Q,R,一般为对角阵;2) 根据式(6)求解矩阵P;3) 计算K=R-1BTP。
从以上步骤可以看出,在确定参数矩阵Q,R之后,LQR控制算法中其余参数均可确定,而Q,R又可取对角阵,因此反馈矩阵K的求取并不复杂。文献[17-19]利用这种方法实现了无人机的位姿控制。
LQR本质上也是一种线性化的方法,在大机动飞行等强非线性的情况下,其控制效果会受到模型不准确的影响。
2.3 滑模控制
滑模控制也称为变结构控制,是一种特殊的非线性控制,最大特点在于“结构不固定”,可以根据系统当前的状态不断地切换控制量,使得系统状态到达滑动模态后沿着预先设定的滑模面运动到平衡点,其系统性能完全由滑模面决定,而与被控系统对象参数和扰动无关。其设计思想为:设计一个控制器,将从任何一点出发的状态轨线通过控制作用拉到滑模面上,然后沿此滑模面滑动到原点。形式为
(7)
式(7)表明,滑模控制算法的设计由控制量函数u+(x),u-(x)及滑模面函数s(x)组成。
对于四旋翼无人机的姿态控制,可设计滑模控制器为
(8)

同理,对于位置滑模控制器亦可建立类似于式(8)的方程,但计算出的控制量u需要线性转化为期望的姿态角。
式(8)中的滑模面函数是位姿变量的一阶函数,称为一阶滑模控制器。此外,文献[21]还探讨了位姿控制的二阶滑模控制器。
利用滑模控制方法设计位姿控制算法可以使系统获得较好的鲁棒性,尤其是对模型不精确以及参数不确定性问题具有较好的抑制效果,但大部分算法还处于仿真阶段,实现难度较大。
2.4 反步法
反步法的设计思想是将复杂的非线性系统分解成不超过系统阶数的子系统,为每个子系统设计李雅普诺夫函数和中间虚拟控制量,然后由低阶从前往后递推进行虚拟控制量的设计,一直后退到最高阶实际控制量的设计。当高阶系统受到实际控制量控制渐进稳定后,低阶系统也会由后往前依次达到稳定状态。
以四旋翼无人机的姿态控制为例,根据反步法可将系统构造为
(9)

姿态方程可视为一个二阶系统,加上最后的控制输出,所以用反步法设计需要以下3步。

2) 由于α1和x2不相等,仿照步骤1)设计虚拟控制量α2代替x3,使α1和x2之间的误差趋近于0,同样利用李雅普诺夫函数设计。
3) 由于x3本身即为可以设计的控制量,所以可以直接令x3=α2。
上述内容介绍了如何利用反步法来设计姿态控制算法,如果设计位置控制算法,可将位置环也视为一个二阶系统,和姿态环一起设计共需5步,位置在前,姿态在后;但考虑到高度和偏航通道是全驱动通道,实际一共分为7步进行算法设计,文献[22]对反步法的位姿控制进行了深入研究。
从式(9)可以看出,反步法可以实现非线性控制,但需要知道模型f(x2)的结构参数。文献[23-25]将反步法用于解决四旋翼的位姿控制以及路径跟踪控制。
2.5 鲁棒控制
鲁棒控制方法大多在PID控制算法等抗扰能力不足的算法上施加鲁棒控制,以提高控制系统的鲁棒性能。
如基于信号补偿的鲁棒控制方法引入一个标称受控对象,将具有不确定性的实际受控对象视为标称受控对象摄动所得,而摄动部分对闭环系统的影响则归结为一个“等价干扰”的影响[26]。首先,忽略等价干扰的影响,对标称受控对象设计出“标称控制器”,实现期望的闭环控制特性;然后,设计出“鲁棒补偿器”产生“鲁棒控制信号”抵消或者抑制等价干扰对闭环控制性能的影响。
对于四旋翼无人机,该方法先将系统数学模型分为容易控制的线性部分和不易控制的不确定部分,其中线性部分类似于式(2),称为标称模型,不确定部分为真实模型式(1)和简化模型式(2)之差,称为干扰模型,然后对标称模型使用PID控制算法,而对干扰模型设计了鲁棒补偿器进行信号补偿,其中鲁棒补偿器的形式为

(10)
式中:F(s)是需要设计的鲁棒滤波器,设计方法可参考文献[27];aN是根据标称模型所确定的参数。图4是姿态鲁棒控制算法的原理框图。
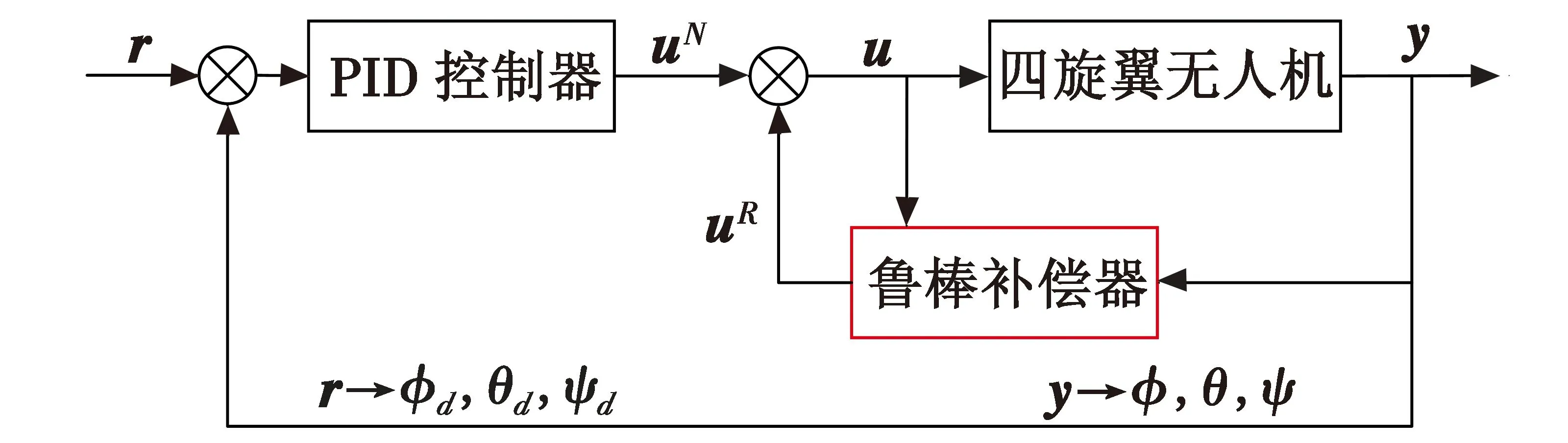
图4 PID控制器和鲁棒补偿器Fig.4 PID controller and robust compensator
图中,r表示参考输入,y表示系统输出。
同理,可实现位置的鲁棒PID控制,对于x,y方向的位置控制,其控制输出即为期望的俯仰角和横滚角φd和θd,文献[28]对此进行了研究。
从图4可看出,该算法不需要知道特别精确的数学模型,对于控制器的设计要求也比较低,易于实现。
2.6 其他方法
除上述四旋翼无人机控制算法之外,还有一些其他的控制方法,如自适应控制、模糊控制、神经网络算法等也被使用在四旋翼无人机的控制算法中。
自适应控制本质上是一个修正装置,一般不独立对系统进行控制,而是与其他常用的控制方法结合,对相关参数或状态进行修正或者调节。如文献[29]在位姿的内外环控制中,自适应控制算法与滑模控制结合组成外环位置控制,与反步法结合组成内环控制。对于自适应算法期望的性能指标则是在控制器的设计过程中,根据李雅普诺夫函数的稳定性要求得出。自适应方法可以很好地在线估计模型参数,但在估计过程中,会有明显的过渡过程,不利于四旋翼无人机的快速机动飞行。
模糊控制的关键在于建立一张控制策略表,四旋翼无人机飞行时,根据飞行状态从控制策略表中选择相应的控制量。虽然不要求建立被控对象的精确数学模型,但是控制策略表由人工设计规则,合理性难以得到保证。
神经网络算法适合处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题。如文献[30]利用PID神经网络算法设计四旋翼飞行器的控制器,并在联合仿真平台上进行仿真,实现对四旋翼飞行器多变量系统的解耦控制,并取得良好的飞行控制效果。
3 飞控算法发展趋势
综上:就应用现状而言,主流的飞控算法仍为PID控制算法,利用PID算法已经可以实现四旋翼无人机的定点悬停、航迹跟踪等;就研究现状而言,四旋翼无人机的非线性控制和鲁棒性能仍是当下研究的热点。
此外,随着市场的需求和技术的发展,可以预见,四旋翼无人机的智能化和集群化控制是飞控算法未来可能的发展趋势。对于智能化发展方向,主要是基于图像传感器的手势识别、目标跟踪、自主避障;基于物联网技术的远程控制、自主起降、自主规划飞行航迹、承担物流运输等任务。对于集群化发展方向,主要是多无人机的编队控制,协同执行大型任务,尤其是军事方面对无人机集群作战的一些构想,近年来已经初见端倪,如通过战机在作战区域投放大量小型无人机,分散攻击多个目标,消耗敌方防御力量。
4 结束语
四旋翼无人机的研究涉及传感器技术、计算机技术、自动控制技术、通信技术、电子电路设计、精密机械设计等多个学科的内容,本文所讨论的飞控算法主要与自动控制技术相关。但各个学科之间相互影响,随着传感器等测量技术、计算机等微电子技术以及机械制造等材料和加工技术的发展,未来飞控算法可以建立更精确的数学模型,许多理论研究成果也能逐步走向工程应用,进而,四旋翼无人机就可以面对更复杂的飞行环境,得到更为广泛的应用,为人类服务。

