一种Adaboost优化的MIMUs/GPS信息融合算法

夏琳琳，赵 耀，马文杰，丛靖宇，肖建磊

(东北电力大学，吉林 吉林 132012)

0 引言

基于MEMS的IMU/GPS组合导航系统尺寸小、可靠性高，可为车载导航系统提供成本较低、精度较高的导航方案[1-3]。由于GPS存在受多路径效应影响、抗干扰能力差、低信噪比等缺点，且陆地载体在运行过程中不可避免地会受到外部环境的干扰(如遇高建筑物遮挡、驶过隧道等)，此时会出现卫星信号接收不良的情况[4-6]。一旦GPS信号发生异常，或接收到信号的卫星数不足以完成卫星定位，工作在“速度-位置”模式下的组合模型将失去意义，整机系统将退化为纯惯性导航工作模式。可以预见的是，由于MEMS惯性测量元件的精度不高，必然会引起导航参数的误差随时间逐渐积累，导航解算精度随之失去保证。为了确保在GPS失锁期间得到持续、高精度的导航信息，具备自适应学习特性的人工神经网络辅助方法越来越多地被引入到导航系统的信息处理中。其中，文献[7-8]采用了基于Bagging的集成学习法开展组合导航系统信息融合问题研究，针对网络训练样本不全面对预测精度造成不利影响的问题，采用放回重抽样方法，实现对多个学习器的集成，通过组合多学习器来强化预测精度，抑制SINS的定位误差。受到上述文献的启发，本文引入Adaboost方法来改进单一的BP神经网络(BPNN)逼近器，在GPS失锁的情况下，对组合滤波器的观测值，即MIMUs与GPS分别输出的速度、位置误差进行预测，并将Adaboost优化的BPNN模型集成到MIMUs中，补偿失锁期间丢失的导航信息。与Bagging类似，Adaboost也是集成学习方法中的一种，它通过迭代，训练出若干弱学习器，再通过加权的方式结合，得到最终的强学习器，改善单一神经网络在训练中存在的不足。与Bagging不同的是，Adaboost更关注训练样本的全面性，其能够根据训练样本的预测效果，不断增加预测效果差的样本权重、降低预测效果好的样本权重，优化整个逼近器的性能。

本文针对GPS失锁时MIMUs/GPS组合导航系统精度急剧下降的问题，在允许系统降低对导航器件精度要求的条件下，通过改进系统层面的导航策略和引入Adaboost的数据处理方法，提高其对系统Kalman滤波观测值的预测精度，确保在不损失系统实时性的前提下，获得理想的导航预测稳定性和滤波精度。

1 MIMUs/GPS组合导航系统

MIMUs是基于MEMS的惯性测量单元，与GPS结合，可看作是低成本的INS与GPS的组合[9]。采用MIMUs/GPS松组合的方式，根据惯性导航误差方程，选取相应的误差作为状态变量，建立系统状态方程；选取MIMUs解算出的速度、位置信息与GPS接收机接收到的速度、位置信息的差值作为观测量，建立观测方程，经Kalman滤波器对系统状态进行估计。

系统的状态方程为

(1)

式中：W(t)为系统噪声，可用白噪声表示；状态转移矩阵F(t)和噪声驱动阵G(t)的详细构成参见文献[10]，这里不再赘述。

对于陆地载体，不对其天向速度和高度信息进行估计，状态变量表示为

X(t)=[ΦEΦNΦUδVEδVNδLδλεrxεryεrz▽x▽y▽z]T

(2)

式中：ΦE，ΦN，ΦU分别为东向、北向、天向的平台姿态角误差；δVE，δVN分别为东向和北向速度误差；δL，δλ分别为纬度和经度误差；εrx，εry，εrz为三轴陀螺仪的漂移；▽x，▽y，▽z分别为三轴加速度计的零偏。

系统的观测方程为

Z(t)=H(t)X(t)+V(t)

(3)

式中：

(4)

VIE，VIN，LI，λI和VGE，VGN，LG，λG分别为MIMU和GPS的东向速度、北向速度、纬度和经度;

(5)

V(t)为观测噪声，可用白噪声表示。系统的结构如图1所示。

图1 组合导航系统结构框图Fig.1 Block diagram of integrated navigation system

图中，wibb为MEMS陀螺仪的输出，f b为加速度计的输出。如上，系统满足线性随机差分，且过程和观测噪声都是高斯白噪声，Kalman滤波器为最优信息处理器。

2 基于Adaboost的BPNN改进算法

2.1 Adaboost算法原理

Adaboost算法实现的具体步骤如下所述。

1) 给定一个训练算法(本文为BP算法)和训练集(本文中的训练集从GPS信号正常时，正常工作的组合导航系统中采集而来)。

2) 初始化训练集中各个训练样本的分布，将初始时的样本分布D1(i)设为均匀分布，设样本总数为N，则

D1(i)=1/N

(6)

式中，i为样本序数。

3) 根据训练样本的概率分布Dt(i)采集训练样本，得到一个弱学习器lt(x)，其中，t为当前迭代次数。

4) 计算在当前得到的学习器下各训练样本的误差e(i)以及误差的平均值et为

(7)

5) 计算当前学习器的权重Wt为

(8)

6) 调整下次迭代时的样本分布，算式为

(9)

对样本分布进行归一化处理，确保各样本的采样概率之和为1。

7) 重复步骤3)～6)，直至迭代次数达到T为止。

8) 将T个弱学习器的权重Wt归一化之后加权结合，得到最终的强学习器L(x)为

(10)

基于Adaboost的BPNN算法流程如图2所示。

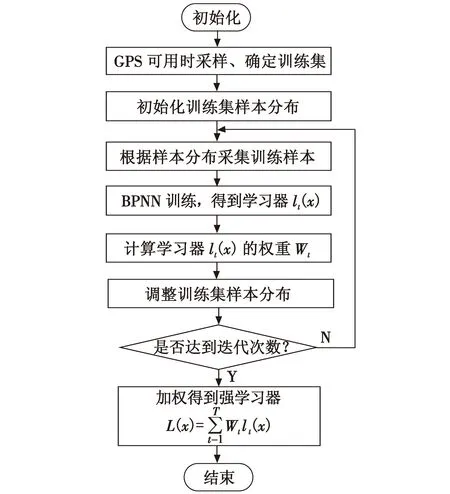
图2 基于Adaboost的BPNN算法流程图Fig.2 Flow chart of Adaboost_BPNN algorithm

2.2 基于Adaboost的BPNN离线训练

在GPS正常工作时，MIMUs/GPS整机系统正常工作，此时采集MEMS陀螺仪的输出wibb和加速度计的输出fb作为训练的输入样本，采集MIMUs解算出的速度、位置信息与GPS接收机的输出值，将二者做差，作为输出期望值，采集足够的样本后，采用BP算法进行一次训练，得到一个学习器，基于此学习器，采用Adaboost方法共进行3次迭代，分别得到弱学习器l1(x)，l2(x)，l3(x)，加权后得到一个强学习器，将该学习器用于GPS失锁时组合导航系统观测值的预测。基于Adaboost的BPNN(Adaboost_BPNN)工作在训练模式下的系统结构如图3所示。

图3 神经网络训练模式下的系统结构图Fig.3 Structural diagram of the system under Adaboost_BPNN training mode

2.3 Kalman滤波观测值的在线预测

GPS失锁时，将MEMS惯性器件的输出作为强学习器的输入，对MIMUs与GPS输出之间的误差，即Kalman滤波的观测值进行在线预测，以保证整个组合导航系统正常运行。此时整个系统的构成如图4所示。

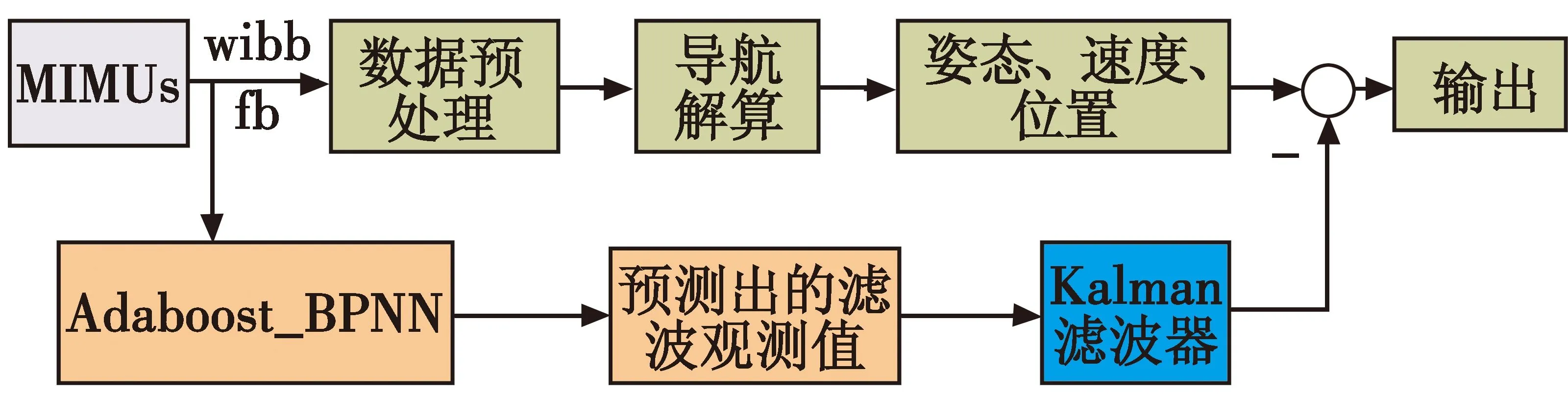
图4 神经网络预测模式下的系统结构图Fig.4 Structural diagram of the system under Adaboost_BPNN prediction mode

图5所示为Adaboost优化的组合导航系统信息融合算法。

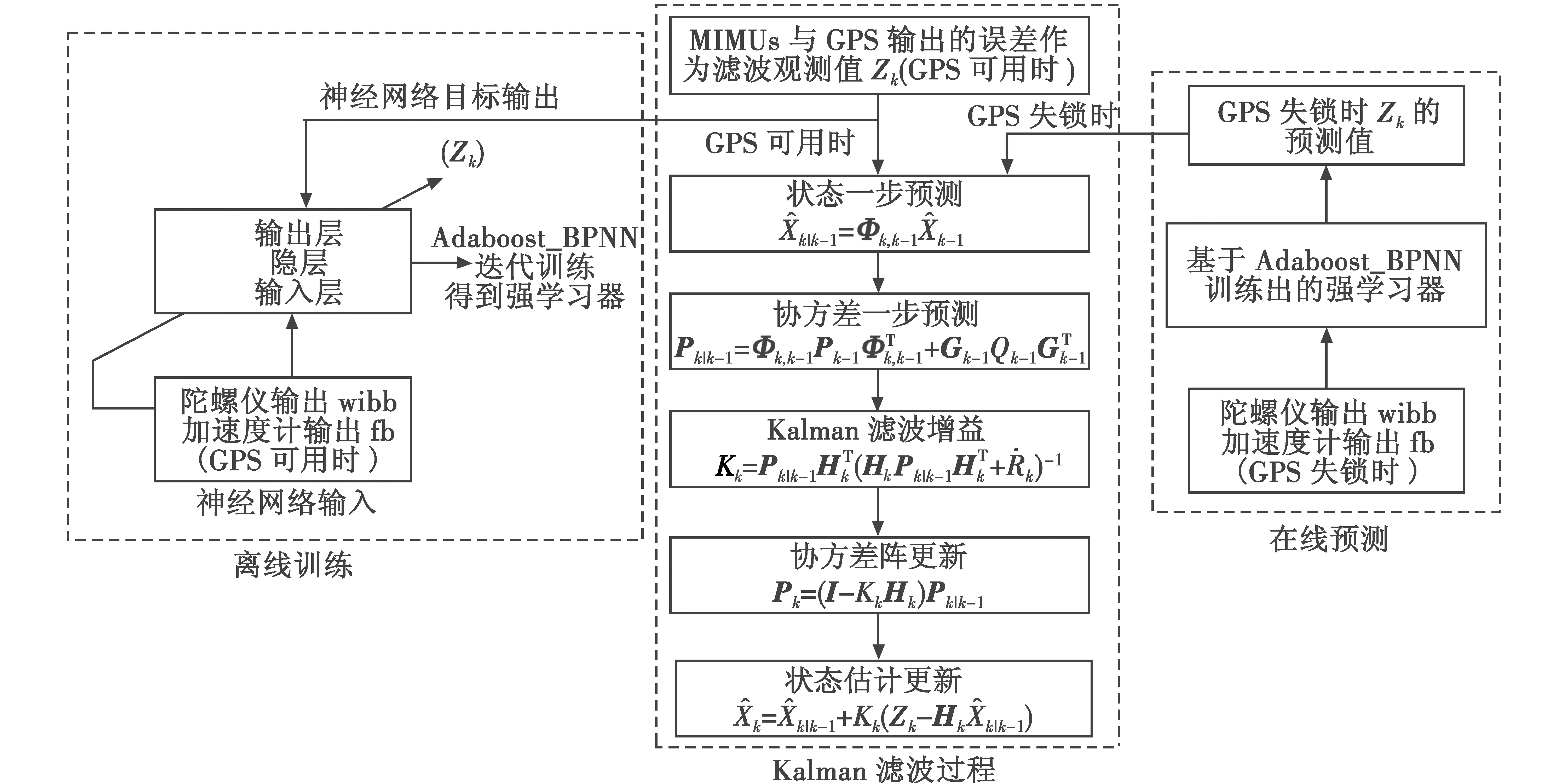
图5 Adaboost优化的组合导航系统信息融合算法框图Fig.5 Block diagram of integrated navigation system information fusion algorithm based on Adaboost optimization

3 算法仿真验证

3.1 仿真环境及参数设置

为进一步验证所提算法的有效性，采用轨迹发生器模拟载体的理想轨迹，将轨迹发生器产生的速度与位置信息加上噪声用以模拟GPS接收机接收到的数据，在Matlab7.1平台上完成算法的仿真验证。设置载体的初始东向速度为VIE0=0 m/s，初始北向速度VIN0=0 m/s，纬度为42.175°，经度为121.226°，初始姿态角均为0°。MIMUs更新周期为0.01 s，GPS更新周期为1 s，陀螺仪漂移为20 (°)/h，加速度计零偏为100×10-6g，仿真总时长为300 s。在150～200 s内，人为设置GPS信号丢失，并设计对比实验来验证本文算法的有效性。

在设计网络时，由于采用了Adaboost算法迭代训练来改善单一BPNN的性能，若BPNN的输出采用多维向量，则可能出现同一组训练样本中各维输出向量训练效果不一的情况，不利于采用Adaboost算法进行样本权值调整。为避免这种情况，经试凑，设计了4个并行的、结构为6-13-1的网络，分别以MIMUs与GPS接收机输出的X，Y方向速度误差和X，Y方向位置误差为训练目标进行训练。参数设置上，4个初始的BPNN训练时均采用梯度下降法，激活函数均选用Sigmoid函数，训练目标误差设置为10-5。

3.2 仿真结果分析

图6为整个仿真周期的300 s内系统导航参数误差曲线图(以东向速度误差曲线为例)。为更清晰、更直观地展现GPS失锁期间不同方法对导航精度的补偿效果，图7、图8分别给出了GPS失锁的150～200 s内经BPNN，RBFNN和本文采用的Adaboost_BPNN方法补偿后的速度和位置误差曲线。表1为采用上述3种方法后的速度、位置误差均值和均方差对比。

从图6～图8可以直观地看出，在0～150 s以及200 s以后，GPS信号正常，系统处于正常的组合模式下，导航参数误差较小且收敛。而在惯性传感器精度有限的情况下，GPS断开的150～200 s内，工作在纯惯性模式下的系统误差迅速发散，第200 s时，东向速度误差已经超过了3.5 m/s，X方向位置误差已经接近350 m，显然无法达到导航系统的精度要求。经上述3种方法补偿后的系统速度、位置误差较之补偿前大大减小，东向速度最大误差控制在0.5 m/s左右，X方向位置误差控制在50 m以内，表明这3种方法均能在GPS失锁期间抑制导航参数误差发散。

表1给出了3种方法的统计数据比较。相同条件下的仿真结果表明，采用Adaboost_BPNN方法后，导航坐标系下东、北向的速度误差，以及地球坐标系下的X，Y方向位置误差的均值及均方差均有更大幅度减小，各项性能指标达到三者最优，其中，Adaboost_BPNN方法下Y方向位置误差均值较RBF方法下提升可达81.0%。同时，尽管BP算法在位置误差均值上的预测效果优于RBF算法，但其均方差较大，表明数据的离散程度大，即BP在预测过程中对误差的补偿效果还不够稳定，本文Adaboost算法经3次BP迭代并经加权获得的强学习器有效解决了这个问题，更适用于GPS失锁阶段的在线预测。

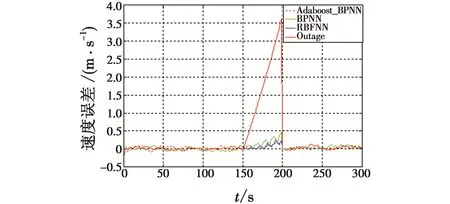
图6 系统东向速度误差曲线Fig.6 Curve of velocity error in the east

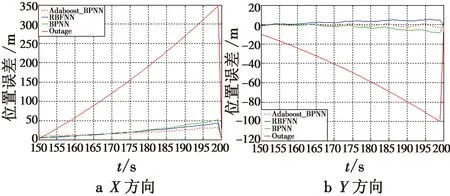
图8 位置误差对比曲线Fig.8 Contrast of position error

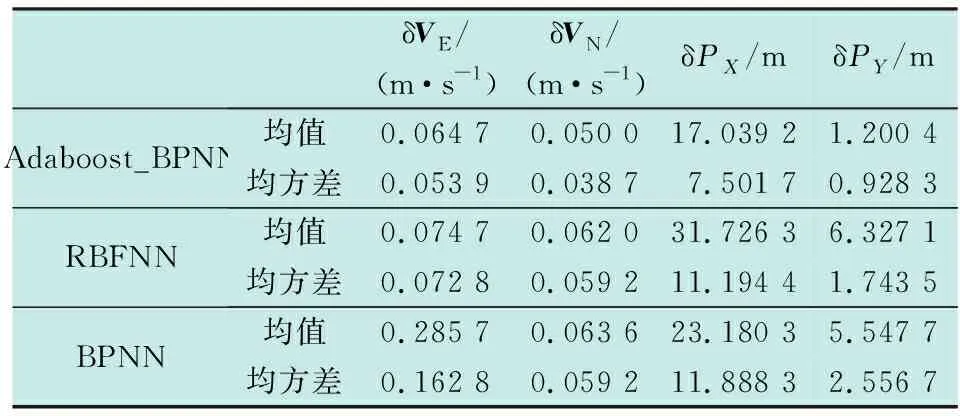
δVE/(m·s-1)δVN/(m·s-1)δPX/mδPY/mAdaboost_BPNN均值0.064 70.050 017.039 21.200 4均方差0.053 90.038 77.501 70.928 3RBFNN均值0.074 70.062 031.726 36.327 1均方差0.072 80.059 211.194 41.743 5BPNN均值0.285 70.063 623.180 35.547 7均方差0.162 80.059 211.888 32.556 7

4 结论

本文以MIMUs/GPS组合导航系统为研究对象，为了优化GPS失锁期间由于MEMS器件精度较低而下降明显的导航精度，引入Adaboost方法改进了单一的BP网络，辅助Kalman滤波器进行信息融合。在GPS可用阶段采集训练样本，基于Adaboost方法对BP神经网络进行迭代训练，并将得到的弱学习器加权结合成强学习器。GPS失锁时利用训练好的强学习器对组合导航系统滤波的观测值进行预测，以保证整个系统正常运行，并用来修正MIMUs的输出结果。对比相同仿真条件下的仿真结果，在GPS断开的50 s内，采用基于Adaboost改进的BP算法能有效地预测出松组合模式下导航系统滤波的观测值，在不损失系统实时性的前提下，确保滤波器具有理想的导航预测稳定性和预测精度。