一类圆锥曲线问题的多种视角探究
☉江苏省曲塘高级中学 万海兵
在解答完一道题目后,尝试从不同的视角探究问题的解答、从不同的角度对题目进行变式探究,是帮助学生巩固知识、提升解题能力的有效方式.圆锥曲线问题是实施多解与多变的有效载体.本文以2018年一道抛物线试题为例说明.
引例 (2018年全国卷Ⅰ)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.
(1)当l与x轴垂直时,求直线BM的方程;
(2)证明:∠ABM=∠ABN.
圆锥曲线既具有代数方程,又具有几何特征,因此问题的求解常可从代数与几何两种视角入手.另外,由于圆锥曲线具有统一的定义、对称性等,因此可对问题从横向、纵向进行深入拓展,也可对相应曲线进行类比探究.本题虽然难度不大,却是我们探究训练的较好载体.本文对第(2)问加以探究.
一、解法探究
视角1:若∠ABM=∠ABN,则直线BM,BN的倾斜角互补,斜率和为0.
证法1:当直线l的斜率不存在时,易知结论成立.
当直线l的斜率存在时,设M(x1,y1),N(x2,y2),l:x=my+2.与抛物线方程联立得消去x,得y2-2my-4=0.
又Δ=(-2m)2+16>0,所以y1+y2=2m,y1y2=-4.
所以∠ABM=∠ABN.
问题得证.
视角2:如图1所示,过点M,N作x轴的垂线,垂足分别为M′,N′.若∠ABM=∠ABN,

图1
证法2:设M(x1,y1),N(x2,y2),不妨令y1>0,y2<0.

以下同证法1,过程略.
评析:证法1从所证结论入手,找到两条直线斜率之间的关系;证法2由∠ABM=∠ABN得到两三角形相似.这两种方法,均从几何视角找到了M,N两点坐标之间满足的关系,从而将几何问题代数化.
视角3:若∠ABM=∠ABN,则由平面向量的数量积公式可得,进而将几何问题代数化.
证法3:设M(x1,y1),N(x2,y2),不妨令y1>0,y2<0=(x1+2,y1)=(4,0)=(x2+2,y2),
由证法1得y1+y2=2m,y1y2=-4,
,问题得证.
评析:解析几何中,如涉及夹角、垂直等有关的问题,常可借助平面向量数量积坐标公式,将几何关系代数化.
二、变式探究
变式1:设抛物线C:y2=2x,点B(-2,0),斜率为k的直线l与C交于M,N两点,与x轴交于点A.
(1)略.
(2)若∠ABM=∠ABN,则点A的横坐标是否为定值?若是,求出该值;否则,说明理由.
解析:设M(x1,y1),N(x2,y2),l:y=kx+m,显然k≠0.
消去y,
得k2x2+(2km-2)x+m2=0.
又Δ=4(km-1)2+4k2m2>0,所以
解得m=-2k.
所以点A的横坐标为定值2.
评析:本例将题目的结论与条件互换,即给出角相等的条件,判断直线是否过定点.此类问题的处理策略是:设出直线方程y=kx+m,根据题目条件得出m,k的关系式,再将直线方程表示成“点斜式”,得出直线所过的定点.
变式2:设抛物线C:y2=2x,点A(2,0),斜率为k的直线l过点A且与抛物线C交于M,N两点.
(1)略.
(2)在x轴上是否存在点B,使得∠ABM=∠ABN?若存在,求出点B的坐标;否则,说明理由.
解析:设B(t,0),M(x1,y1),N(x2,y2),l:x=my+2(m≠0),与抛物线方程联立得消x得y2-2my-4=0.
又Δ=(-2m)2+16>0,所以y1+y2=2m,y1y2=-4.
,且x1=my1+2,x2=my2+2,
所以t=-2,即点B的坐标为(-2,0).
评析:本题将结论与条件互换,探究点B的存在性.此类探索性问题的求解,可先假设探究的定点存在,并用参数表示点的坐标,结合已知条件构建含参的方程,进而得出参数的值,即定点坐标.若构建的方程无解,或所得解与已知条件矛盾,则说明满足条件的点不存在.
三、结论探究
结论:设F为抛物线C:y2=2px(p>0)的焦点,过点F的直线与C交于A,B两点,点O为坐标原点,则∠AMO=∠BMO.
用以上几种方法可证明此结论,过程略.
类似地,还可以将此结论推广到椭圆和双曲线:
下面用引例中的视角1,对此结论进行证明.
证明:设直线AB:x=my+c,A(x1,y1),B(x2,y2).
(b2m2+a2)y2+2b2mcy-b4=0.
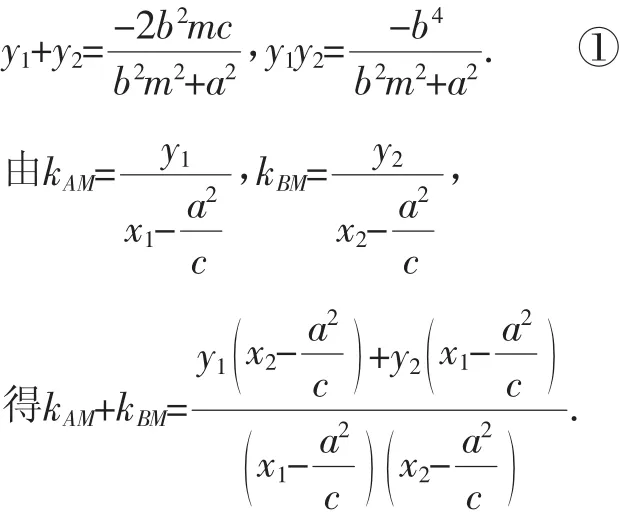
由根与系数的关系得由x1=my1+c,x2=my2+c,得


所以∠AMO=∠BMO.命题得证.
请读者自行完成此命题的证明.
综上所述,通过对一道题目从多种不同的视角进行解答、将背景变换进行探究,不仅得到了一般结论,促进了知识体系的形成,也拓展了我们的知识面,提升了解题能力.W

