Rashba自旋轨道耦合下square-octagon晶格的拓扑相变∗

杨圆1)2)† 陈帅1) 李小兵1)

1)(江苏科技大学张家港校区,张家港 215600)

2)(南京大学,固体微结构物理国家重点实验室,南京 210093)

(2018年4月9日收到;2018年10月2日收到修改稿)

1 引 言

拓扑绝缘体是一种新的量子物质态,其体电子态是有能隙的绝缘态,而其边界或表面是无能隙的金属态[1−5],这种金属态是由能带结构的拓扑性质决定的,受到时间反演对称性的保护.量子自旋霍尔效应,即二维的拓扑绝缘体,是通过自旋轨道耦合来实现的,其拓扑性质可以由Z2不变量[6,7]或者自旋陈数[8−10]刻画.对于时间反演对称的电子系统,Z2指标和自旋陈数给出完全等价的描述.但是在时间反演对称性被破坏的情况下,将无法定义Z2拓扑不变量,而自旋陈数的鲁棒性依然保持不变[8].最近,自旋陈数被用于描述交换场作用下量子自旋霍尔效应的拓扑性质[11].研究结果发现,在时间反演对称性被破坏后,量子自旋霍尔态的非平庸拓扑性质仍然存在.这种时间反演对称破缺的量子自旋霍尔效应在弱无序情况下,其边界上的螺旋边缘态结构依然是稳定的.实验上也在InAs/GaSb量子阱中证实了时间反演对称性破缺的量子自旋霍尔效应的稳定性[12].

石墨烯的内禀自旋轨道耦合强度非常弱[13−15],而破坏镜面对称性的外禀Rashba自旋轨道耦合作用也不利于实现量子自旋霍尔效应[6].但是,在石墨烯中通过引入Rashba自旋轨道耦合和破坏时间反演对称性的交换场,可以实现一种无朗道能级的量子霍尔效应,即量子反常霍尔效应[16,17].量子反常霍尔效应边缘态具有手征的特征.当Rashba自旋轨道耦合和交换场同时存在时,人们在kagome晶格[18],star晶格[19]和Lieb[20]晶格中也发现了量子反常霍尔态.

在HgTe/CdTe量子阱中发现量子自旋霍尔效应之后,一些新的二维拓扑绝缘体也相继被提出,比如kagome晶格[21]、修饰的蜂窝状晶格[22]和单层锑异质结构等[23].近年来,square-octagon晶格凭借其独特的几何结构吸引了一些理论工作者的研究兴趣,并得到了许多有意义的结果[24−30].例如,Kargarian和Fiete[24]研究了具有自旋轨道耦合的square-octagon晶格中的拓扑相;Bao等[26,27]利用团簇动力学平均场理论和连续时间量子蒙特卡罗算法,描述了温度和相互作用对squareoctagon晶格中电子行为的影响.然而到目前为止,Rashba自旋轨道耦合作用和交换场对squareoctagon晶格的拓扑性质的影响还未被研究.另一方面,随着实验条件的改善和实验技术的发展,二维蜂窝状六角晶格[31]和kagome晶格[32]可以通过操纵光晶格中的超冷原子来构建,因此我们相信square-octagon晶格在不久的将来能够在实验中得以实现.特别的是,实验上发现功能材料ZnO具有准square-octagon结构[33].因此,本文将研究各向同性square-octagon晶格在内禀自旋轨道耦合、Rashba自旋轨道耦合和交换场作用下的拓扑相变,本工作的研究能够加深对square-octagon晶格以及准square-octagon结构材料的认识.

本文将证明考虑Rashba自旋轨道耦合作用和交换场时,各向同性square-octagon晶格也会支持量子自旋霍尔效应的存在,并且处于不同填充因子时可以实现不同的拓扑相.利用陈数和自旋陈数确定系统的拓扑性质,同时为了验证各种拓扑相的存在,计算了square-octagon晶格的边缘态能谱以及自旋性质.计算结果表明,在镜面对称性和时间反演对称性都被破坏的情况下,量子自旋霍尔效应中边缘态的能谱可以是无能隙的,而其对应的自旋谱存在着谱隙.进一步调节交换场的大小,系统会发生从螺旋边缘态到自旋过滤的手征边缘态的拓扑相变,这为自旋量子调控提供了一种新的思路.

2 模型和方法

2.1 紧束缚模型

本文考虑的晶格结构如图1(a)所示.1,2,3,4表示一个原胞内的四个不等价原子,与其对应的第一布里渊区如图1(b)所示,高对称点为Γ,X和M,紧束缚哈密顿量可以表示为[1,6,24,30]

其中

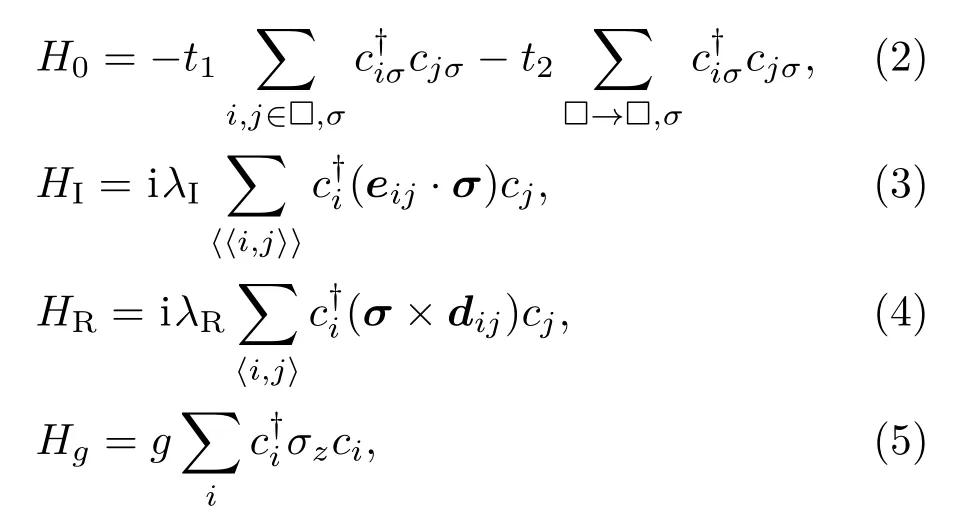
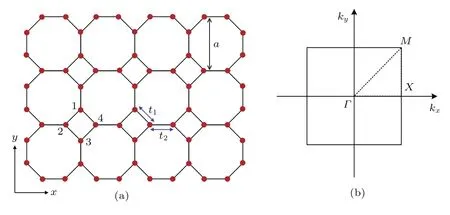
图1 Square-octagon晶格 (a)结构示意图;(b)第一布里渊区Fig.1 .Square-octagon lattice:(a)Structure sketch;(b)the f i rst Brillouin zone.

在傅里叶变换下,选择基矢量

Ψk=(c1k↑,c2k↑,c3k↑,c4k↑,c1k↓,c2k↓,c3k↓,c4k↓)T,实空间哈密顿量在动量空间可以写成H =H(k)Ψk.H(k)表示为

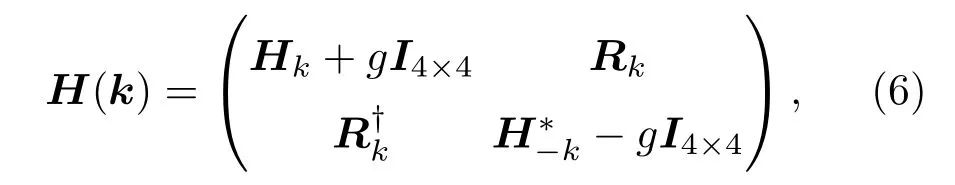
其中I4×4为4×4单位矩阵,Hk和Rk的具体形式如下

其中

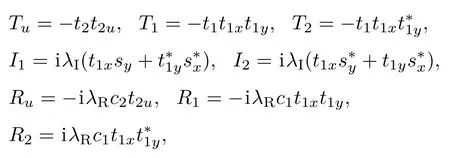
2.2 自旋陈数和边缘态

随着对拓扑绝缘体的深入研究,可以根据不同的拓扑不变量对绝缘态进行分类.本文采用的拓扑不变量是陈数和自旋陈数.量子霍尔系统的拓扑不变量由陈数来表征,但对量子自旋霍尔系统,需要通过Z2拓扑数或者自旋陈数来刻画.对于时间反演对称的系统,自旋陈数和Z2指标是完全等价的.但是在时间反演对称性被破坏后,不便再定义Z2拓扑数,而自旋陈数不依赖于任何对称性,因此可以利用自旋陈数的概念,定义自旋陈数Cs=(C+−C−)/2,其中C±是自旋sz= ±1的能带在第一布里渊区的Berry相位除以2π[8−10].自旋陈数被两个谱隙所保护,一个是导带和价带之间的带隙,另一个是自旋谱隙.自旋谱隙指的是自旋投影算符PσzP本征值的谱隙.只要满足体能隙和自旋谱隙不为零,都可以定义自旋陈数.这里陈数C=C+−C−的计算可以采用已经发展成熟的数值方法[34,35].另一方面,研究系统的拓扑相变的另外一个有效的方法是计算边缘态的能谱,拓扑绝缘体的边缘态也直接跟体能带的拓扑性质有关[36,37].为了研究边缘态的性质,计算一个二维纳米带的能谱,其中y方向宽度为50个原胞,x方向为无限长,因此x方向的动量kx是好量子数.对于每一个动量值kx,通过精确对角化系统的哈密顿量H(kx),可以得到能谱E(kx)和对应的波函数边缘态的自旋极化可以通过来描述.

3 数值结果与分析

3.1 时间反演对称破缺的量子自旋霍尔效应

首先,考虑内禀自旋轨道耦合项λI对色散关系的影响.对角化哈密顿量H(k)可以得到squareoctagon晶格在第一布里渊区中沿着图1(b)所示的高对称点的色散关系,如图2所示.系统中不存在Rashba自旋轨道耦合和交换场时,即λR=g=0,对应的四个能带二重简并.当λI=0时,最上面的三个能带和最下面的三个能带在Γ点和M点接触(图2(a)),能带中不存在能隙,说明系统处于金属态.当λI=0.1时,如图2(b)所示,中间的两个能带在布里渊区中的所有点都是彼此分开的,但它们之间仍然不存在完整的能隙,即有一个负的能隙,因此它们的霍尔电导不是量子化的,系统整体表现为半金属[38].相反,最上面和最下面的两个能带相互分开,产生完整的能隙,表明这时系统处于一种绝缘态.继续增加Rashba自旋轨道耦合至λI=0.6时,如图2(c)所示,系统的四个能带独立存在,彼此分开,并且有很大的能隙.接下来同时引入Rashba自旋轨道耦合和交换场,研究square-octagon晶格在自旋轨道耦合作用和交换场的影响下可能发生的拓扑相变.取参数λI=0.6,λR=0.05,g=0.1,如图2(d)所示,自旋向上与自旋向下的能带完全分开,系统在1/4,1/2和3/4填充时均处于绝缘态.

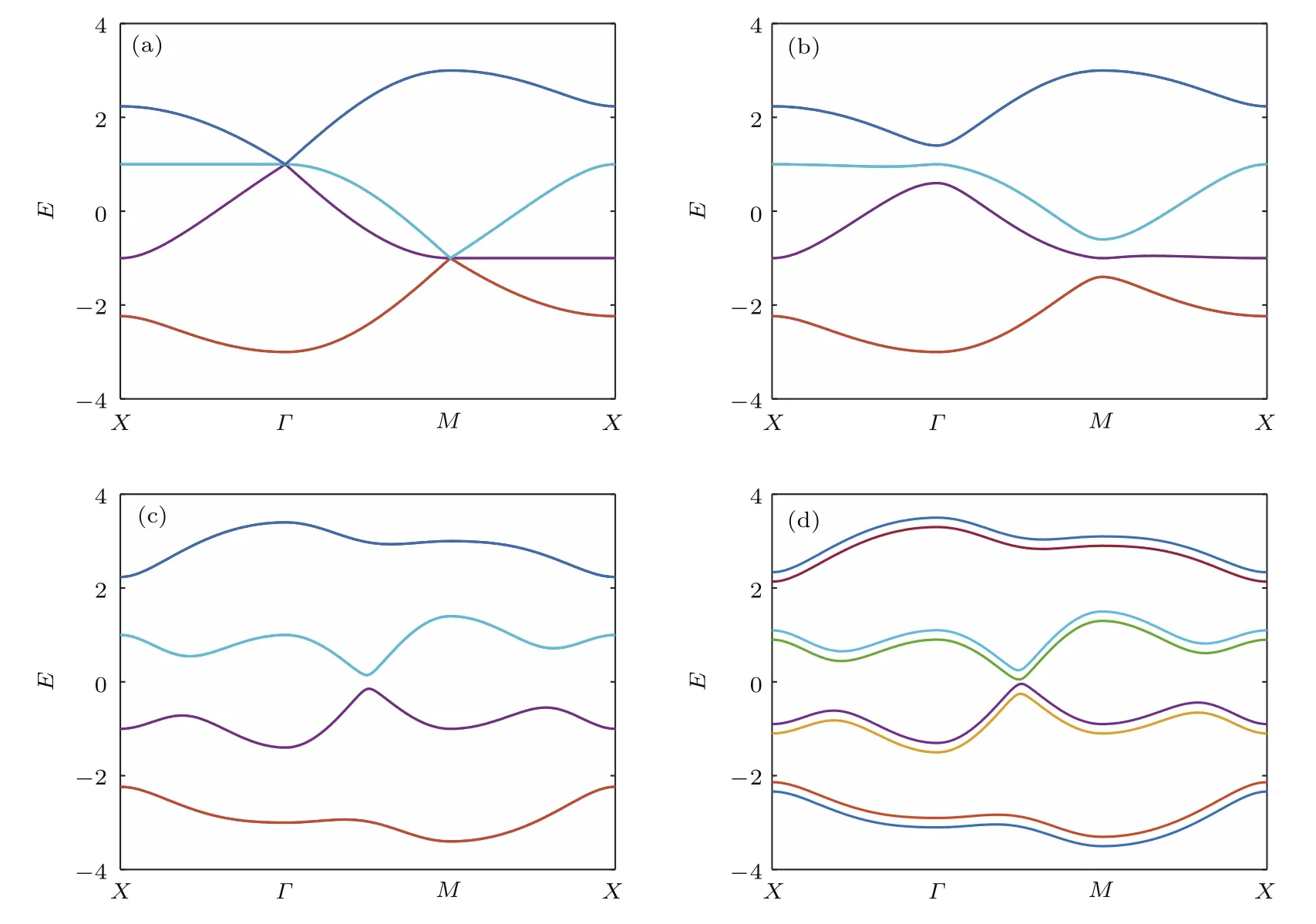
图2 Square-octagon晶格在第一布里渊区内的色散关系 (a)λI=0;(b)λI=0.1;(c)λI=0.6;(d)λI=0.6,λR=0.05,g=0.1Fig.2 .Energy band of square-octagon lattice along the line between high symmetric points in the f i rst Brillouin zone:(a)λI=0;(b)λI=0.1;(c)λI=0.6;(d)λI=0.6,λR=0.05,g=0.1.

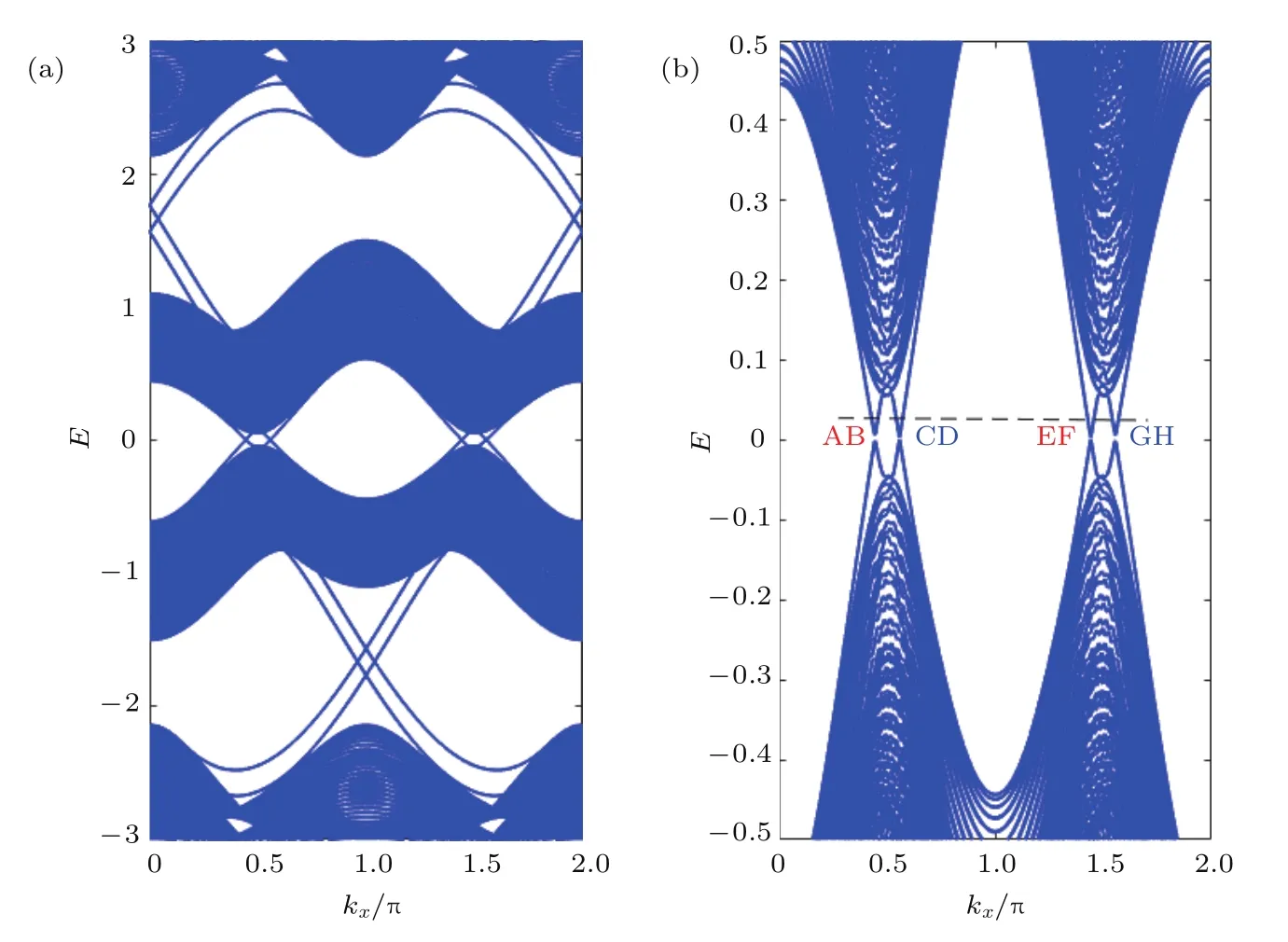
图3 参数λI=0.6,λR=0.05,g=0.1情况下的square-octagon晶格 (a)边缘态能谱;(b)1/2填充时的边缘态Fig.3 .Square-octagon lattice for λI=0.6, λR=0.05,and g=0.1:(a)Energy spectrum;(b)edge states at 1/2 f i lling.

为确定系统是否为拓扑绝缘体,又计算了square-octagon晶格在参数λI=0.6,λR=0.05,g=0.1下的边缘态模式,结果如图3所示.系统在1/2填充时,对于给定的费米能级,很明显有八个不同的边缘态穿过能隙.在图3(b)中,用A到H从左到右依次标记这八个边缘态.为了清楚地了解边缘态的模式,给出了边缘态波函数|ϕ|2在纳米带格点的概率分布和边缘态的自旋极化,如图4所示.发现边缘态A,B,E和F局域在纳米带的一个边界上,而C,D,G和H局域在另一个边界上.以边缘态A和边缘态B为例,从能带中A点和B点的斜率(即速度)很容易知道边缘态A和边缘态B是沿着相反的方向运动的.边缘态的自旋极化标注在图4(a)—图4(h)中,尽管在考虑Rashba自旋轨道耦合作用λR以及交换场g之后,自旋在x和y方向的分量不再为零,但是z方向的自旋极化仍然占有很高的比率.我们发现边缘态A自旋向下而边缘态B自旋向上.以同样的道理可以分析边缘态E和边缘态F的情况.最后总结出,在纳米带的一个边界上,边缘态A和B以及边缘态E和F是两对沿着相反方向运动并且自旋极化方向相反的螺旋边缘态,即N↑=N↓=2,这与计算所得的自旋陈数Cs=2相对应,因此系统处于时间反演对称破缺的量子自旋霍尔相[11].类似地,系统在1/4和3/4填充时,计算得到Cs=−1,这时在纳米带的每个边界上存在着一对反向传播的具有相反自旋极化的边缘态,如图3(a)所示,系统展现同样的量子自旋霍尔效应.

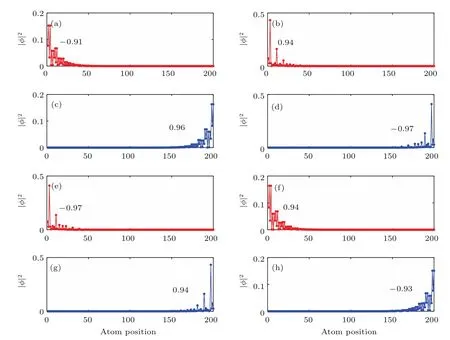
图4 边缘态波函数|ϕ|2在纳米带格点的的概率密度分布和边缘态的自旋极化 (a)边缘态A;(b)边缘态B;(c)边缘态C;(d)边缘态D;(e)边缘态E;(f)边缘态F;(g)边缘态G;(h)边缘态HFig.4 .Probability density of the edge-state wavefunction|ϕ|2of an ribbon and the spin polarizations of the edge states:(a)Edge state A;(b)edge state B;(c)edge state C;(d)edge state D;(e)edge state E;(f)edge state F;(g)edge state G;(h)edge state H.

3.2 自旋过滤的量子反常霍尔效应

图5 不同交换场下square-octagon晶格的边缘态能谱以及1/4填充因子下的相图 (a)λI=0.6,λR=0.05,g=0.8;(b)λI=0.6,λR=0.05,g=1.8;(c)λI=0.6,其中QSH表示量子自旋霍尔绝缘体,QAH表示量子反常霍尔绝缘体,黑色部分表示金属Fig.5 .Edge state spectrum with dif f erent values of exchange f i eld and phase diagram of the square-octagon lattice at 1/4 f i lling:(a) λI=0.6,λR=0.05,g=0.8;(b) λI=0.6,λR=0.05,g=1.8;(c) λI=0.6.Here,QSH denotes the quantum spin Hall insulator,QAH denotes the quantum anomalous Hall insulator and the black color denotes a metal phase.

图6 边缘态波函数|ϕ|2在纳米带格点的概率密度分布和边缘态的自旋极化 (a)边缘态A;(b)边缘态B;(c)边缘态C;(d)边缘态D;(e)边缘态E;(f)边缘态FFig.6 .Probability density of the edge-state wavefunction|ϕ|2of an ribbon and the spin polarizations of the edge states:(a)Edge state A;(b)edge state B;(c)edge state C;(d)edge state D;(e)edge state E;(f)edge state F.

增加交换场的大小,当g=0.8时,边缘态能带结构如图5(a)所示.在3/8填充时,能隙中存在六个边缘模式,分别标记为A,B,C,D,E和F,其波函数空间分布见图6.很容易看出,边缘模式A,C和E局域在纳米带的一个边界上,沿着同一方向运动,而B,D和F局域在另一个边界上,共同沿着另一相反的方向运动,此时纳米带边界存在手征的边缘态模式,因此系统处于量子反常霍尔态,计算得到陈数C=3.特别的是,边缘态自旋向上的数目不等于自旋向下的数目,即N↑=1,N↓=2,从而贡献自旋霍尔电导σSH=−e/4π,霍尔电导σH=3e2/h[39,40].类似地,在5/8填充时,N↑=2,N↓=1,对应C=−3.同时注意到,在1/8填充的情况下,纳米带的每个边界上只有一条自旋向下的边缘态,即N↑=0,N↓=1,计算得到C=−1,这意味着系统处于自旋过滤的量子反常霍尔态[39,40].相反,在7/8填充时,只有一条自旋向上的边缘态存在于边界上,即N↑=1,N↓=0,对应陈数C=1,如图5(a)所示.继续增大交换场至g=1.8,如图5(b)所示,在1/2填充时,系统处于时间反演对称破缺的量子自旋霍尔态,自旋陈数Cs=−1.系统在1/4填充时,纳米带的每个边缘上有两条自旋向下的边缘态沿着同一方向传播,即N↑=0,N↓=2,计算陈数C=2,系统处于自旋过滤的量子反常霍尔态.同样地,系统在3/4填充时处于C=−2的自旋过滤的量子反常霍尔态.本文还通过直接计算各个参数下的陈数和自旋陈数,给出了square-octagon晶格处于1/4填充因子下的相图.图5(c)给出的相图是Rashba自旋轨道耦合作用λR和交换场g的函数.从相图中可以看到,square-octagon晶格支持量子自旋霍尔绝缘体和量子反常霍尔绝缘体的存在,并且Cs=−1的量子自旋霍尔相到C=2的量子反常霍尔相的转变伴随着体能隙的闭合.

将图3(b)和图5(b)中1/2填充时的量子自旋霍尔态相比较,可以看出,在边缘上发生两种情况:一种情况是边缘态能隙打开,导致有能隙的边缘态;另一种情况是在边界上出现无能隙边缘模式.投影自旋算符的矩阵元是〈ϕm(kx)|σz|ϕn(kx)〉,m和n遍历所有被电子占据的态,通过对该矩阵对角化,可以得到自旋谱.对应于图3(b)和图5(b)中给定的参数,计算获得的自旋谱如图7(a)和图7(b)所示.在图7(a)中,当边缘态能谱存在能隙时,自旋谱没有出现能隙.对于无能隙的边缘态,自旋谱只有两个值±1,存在谱隙,如图7(b)所示.因此量子自旋霍尔效应边缘态能谱或自旋谱两者之一必然表现出无谱隙的特征[41].

图7 量子自旋霍尔边缘态的自旋谱 (a)有能隙边缘态;(b)无能隙边缘态Fig.7 .Spin spectrum of quantum spin Hall edge state:(a)Gapped edge state;(b)gapless edge state.

4 结 论

基于陈数和自旋陈数,本文研究了squareoctagon晶格在自旋轨道耦合和交换场作用下的拓扑相变.在自旋轨道耦合和交换场的共同作用下,系统出现许多不同的拓扑相,包括自旋陈数Cs=−1,2的时间反演对称破缺的量子自旋霍尔相和陈数C=±3,±2,±1的量子反常霍尔相.有趣的是,调节交换场的大小或者填充因子,系统发生了从螺旋量子自旋霍尔边缘态到自旋过滤的手征量子反常霍尔边缘态的相变.对于量子自旋霍尔系统,在镜面对称性和时间反演对称性都被破坏的情况下,其边界上的螺旋边缘态可以是无能隙的,而对应的自旋谱存在着很大的谱隙.二维纳米带的边缘态能谱和自旋谱与陈数和自旋陈数的拓扑表征相符合.

量子自旋霍尔效应在不受时间反演对称性保护的情况下,仍然可以存在无能隙的螺旋边缘态,这进一步拓宽了量子自旋霍尔效应的理论框架,为实现稳定的量子自旋霍尔效应提供了一个新方案.同时,square-octagon晶格具有一定的潜在应用价值,研究者已经在功能材料ZnO的(10¯10)中发现准square-octagon结构.另外,在一定的参数范围内,square-octagon晶格中可以出现具有高平坦率的拓扑平坦能带,为研究分数量子反常霍尔效应提供了一个新的晶格模型.就在最近,人们预言在square-octagon晶格中可以实现单轨道高温s±超导态[29].此外,本工作的研究方法可以延伸推广到其他典型的晶格系统[42,43],因此进一步探索square-octagon晶格中其他可能的拓扑非平庸态,例如分数量子反常霍尔态以及其他晶格中可能发生的奇异相变,将是很有意思的工作.而且,由于光晶格冷原子技术的发展,实验上已经可以利用光晶格模拟Haldane模型[44],并且自旋轨道耦合和均匀磁场可以由激光和冷原子间相互作用来调控[45,46],为在实验上观测到这些拓扑相变和自旋操控提供了平台.