五阶压控忆阻蔡氏混沌电路的双稳定性∗
林毅 刘文波 沈骞
(南京航空航天大学自动化学院,南京 211106)
(2018年7月4日收到;2018年8月29日收到修改稿)
1 引 言
忆阻的概念是蔡少堂教授在1971年首次提出的[1],并由惠普实验室在2008年首次证实了忆阻物理器件的可实现性[2].忆阻的发现是经典电路基础理论的重大突破,促进了全新的电路设计与应用的发展.然而,忆阻器的物理工艺难度大、制造成本高等缺点,使得忆阻目前还不能作为分立电路元件应用于实际电路中.因此,研究能够呈现出忆阻特性的、可物理实现的等效模拟电路是十分必要的.近年来,利用现有的电阻、电容、电感、运算放大器和模拟乘法器等分立元器件实现了理想的流控或压控忆阻[3−7]、广义的压控忆阻[8−10]和非理想压控忆阻[11−13]等多种类型的忆阻模拟器,为忆阻及其应用电路的建模分析和实验测量作出了重要贡献[14].
忆阻的非线性使得基于忆阻的电路很容易实现混沌振荡,产生复杂的非线性现象.因此,通过将具有不同非线性特性的忆阻引入到现有的振荡电路中,大量的忆阻应用电路被提出,并取得了丰硕的研究成果[11,15−24].其中,蔡氏电路的电路结构简单,仅由三个动态元件、一个电阻和一个非线性电阻组成,却能够呈现出丰富的分岔和混沌行为,使得各种基于蔡氏电路的忆阻电路得到了广泛的研究[11,15−21].采用数值仿真、电路仿真和硬件实验测量等手段揭示了这些电路中存在的倍周期分岔[16]、自激振荡[16,17]、隐藏振荡[15,17]、瞬态混沌[18]和超混沌[19,20]等一些复杂的动力学行为.文献[15]利用一个非理想压控忆阻[11−13]替换蔡氏电路中的蔡氏二极管,提出了一种改进型压控忆阻蔡氏电路.特别地,该电路有一个零平衡点和两个非零平衡点,其中两个非零平衡点的稳定性会随着电路参数的演化从不稳定的鞍焦转变成稳定的结焦,致使隐藏吸引子[15,25−28]的产生.文献[11]在文献[15]的基础上,进一步对改进型压控忆阻蔡氏电路中的共存多吸引子[11,29−31]现象进行了研究.目前,忆阻电路中依赖于初始状态的共存多吸引子和多稳定性现象成为了一个重要的研究课题,得到了研究者的极大关注.
共存多吸引子意味着在固定的非线性动力学系统参数下,系统存在不同种类的吸引子,每一种都是从对应于不同吸引盆的初始状态激发生成的,显示出非线性动力学系统的双稳定性[32]或多稳定性[33,34].双稳定性或多稳定性是一种奇特的现象,在参数确定的非线性动力学系统中共存了超过一种渐近的稳定状态[33],体现了系统动力学行为对初始条件的敏感性.在实际应用中,一方面可作为信息工程应用的随机信号源[31]或用于图像去噪与对比度强化处理[35]等,为工程应用设计提供更多的灵活性;另一方面也会导致应用系统工作状态的不稳定,是一些实际非线性动力学系统在工程应用时所不期望产生的现象.然而,忆阻电路的多稳定性研究尚处于起步阶段,基础理论和实际应用亟待完善与挖掘.因此进一步开展忆阻电路多稳定性的现象揭示、吸引盆初始状态定位及多稳定状态控制策略等研究显得尤为重要.
已有文献中电路系统的双稳定性或多稳定性是在不稳定平衡点和稳定平衡点同时存在的情况下发生的,各个平衡点邻域各自形成混沌、周期、准周期与稳定点等互不连通的吸引盆[11,29,32].例如,文献[11]报道的改进型压控忆阻蔡氏电路有一个零平衡点和两个对称的非零平衡点,在全局可调归一化参数区域内零平衡点总是不稳定的鞍点,而两个非零平衡点总是稳定的结焦,从而导致多稳定性现象的产生;文献[32]报道的三阶改进型忆阻文氏桥振荡电路有一条线平衡点,线平衡点上分布了三种不稳定区域和一种稳定区域,致使双稳定性现象的产生.而受文献[11,15]的启发,本文提出了一种新颖的五阶压控忆阻蔡氏混沌电路.令人惊奇的是,该电路在给定参数下有且仅有一个不稳定的零平衡点,却形成了混沌与周期的非对称吸引子共存的吸引盆,使得双稳定性现象出现,这是以往文献少有报道的.此外,双稳定性作为一类特殊的多稳定性现象,目前除了文献[32]报道了三阶改进型忆阻文氏桥振荡器中存在的混沌吸引子和点吸引子共存的双稳定性现象,鲜有文献涉及忆阻电路的双稳定性研究.因此,深入研究本文电路的双稳定性特性具有很强的时效性,能够有效促进忆阻电路基础理论的发展和完善.本文首先利用理论分析、数值仿真、电路仿真和常规的动力学分析手段(包括分岔图、相轨图、吸引盆等)着重对电路中的双稳定性现象进行了研究.然后,介绍了电路的实现方案,并基于电路的数学模型,对电路的平衡点和稳定性进行了分析研究,继而探讨了电路在不同初始状态下表现出的动力学特性.最后,建立了归一化系统模型,通过分岔图、相轨图和吸引盆揭示了五阶压控忆阻蔡氏系统产生的双稳定性现象,深入研究了系统依赖于初始条件的动力学行为,并对本文的研究内容进行了总结.
2 五阶压控忆阻蔡氏混沌电路
2.1 电路的实现方案
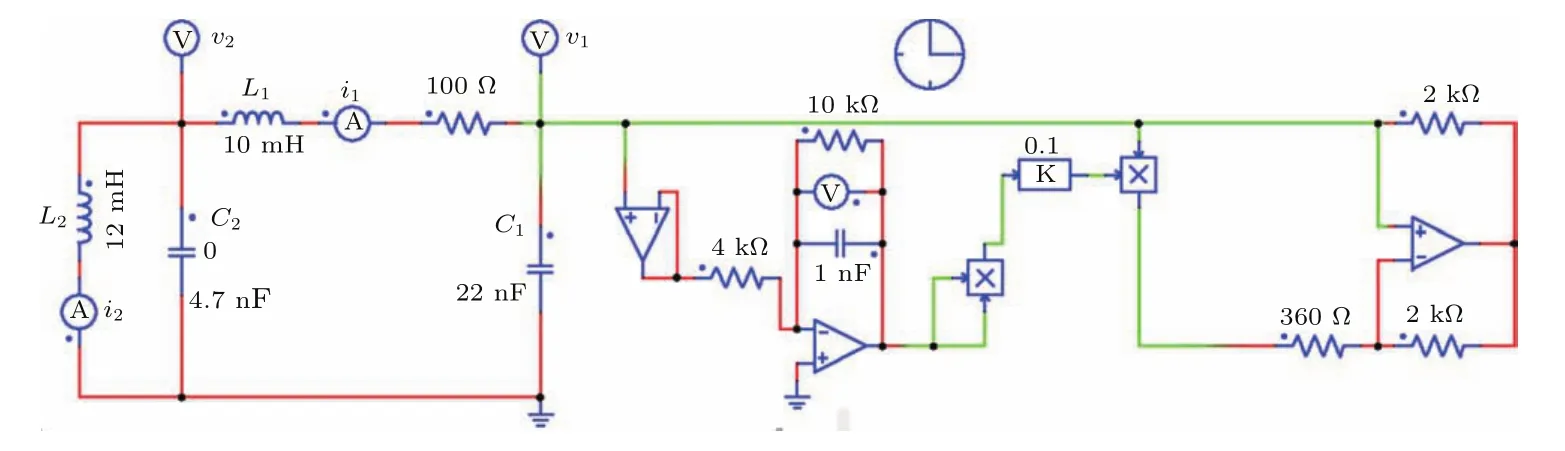
本文在经典三阶蔡氏电路的耦合电阻支路中串联一个电感,采用非理想有源压控忆阻替换蔡氏电路中的蔡氏二极管构建了如图1所示的五阶压控忆阻蔡氏混沌电路.

图1 五阶压控忆阻蔡氏混沌电路Fig.1 .Fifth-order voltage-controlled memristor-based Chua’s chaotic circuit.
如图2所示,一个非理想有源压控忆阻W的等效实现电路是由一个缓冲器Ua、一个连接两个电阻Ra,Rb和一个电容C0的积分器Ub、两个乘法器Ma和Mb、一个连接三个电阻Rc,Rd和Re的电流反转器Uc构成的.不同于理想有源磁控忆阻的等效实现电路[36],该非理想有源压控忆阻等效实现电路在积分电容C0上并联了一个电阻Rb,以避免积分器Ub的直流电压积分漂移[15].
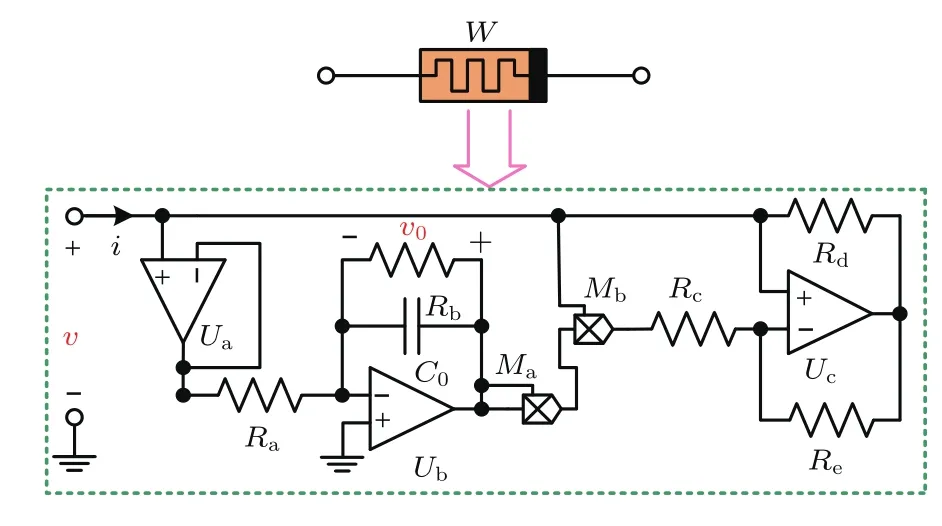
图2 非理想有源压控忆阻等效实现电路Fig.2 .Equivalent realization circuit of the non-ideal active voltage-controlled memristor.
非理想有源压控忆阻的数学模型可描述为
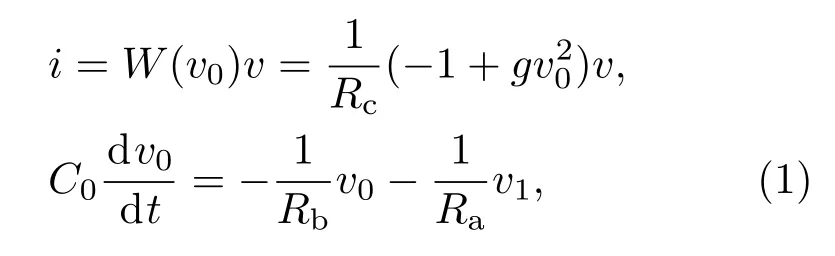
式中W(v0)为忆导函数;v和i分别为非理想有源压控忆阻等效实现电路输入端的电压和电流;v0为积分电容C0两端的电压;g为乘法器Ma与乘法器Mb的总比例因子.该数学模型符合一类广义忆阻的定义式[37].
2.2 数学建模与稳定性分析
图1所示的五阶压控忆阻蔡氏混沌电路有电容C1、电容C2、电感L1、电感L2和非理想有源压控忆阻W内部电容C0五个动态元件,分别对应于五个状态变量v1,v2,i1,i2和v0.根据基尔霍夫电压、电流定律以及电路元件的本构关系,可建立起相应的状态方程组为
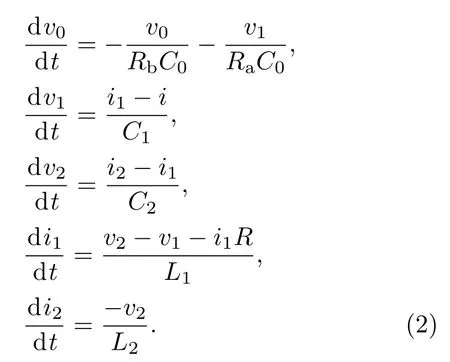
根据(2)式所描述的状态方程组进行理论分析和数值仿真,进而研究五阶压控忆阻蔡氏混沌电路的非线性现象以及动力学特性.
为了求出(2)式状态方程组的平衡点,令等式右边为零,可得到如下关系式:
显然,(2)式存在一个零平衡点S0=(0,0,0,0,0).由(6)式和(7)式可得
结合(8)式和(4)式,可得
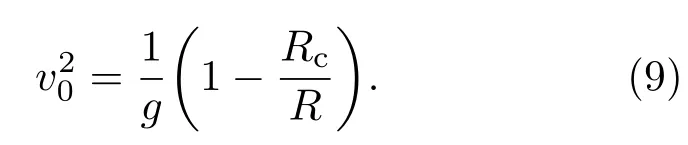
根据(9)式可知,当Rc 式中η=1−Rc/R.当Rc>R时,(2)式有且仅有一个零平衡点,即S0=(0,0,0,0,0).此结果说明,五阶压控忆阻蔡氏混沌电路的平衡点个数和位置与电路参数Rc与R的比值有关,即随着Rc/R的值从小于1逐渐增加到大于1,(2)式的平衡点由起初的一个零平衡点和两个非零平衡点逐渐转变为有且仅有一个零平衡点,且两个非零平衡点的位置随Rc/R的值的变化而不断改变,完全不同于常规的忆阻混沌电路所具有的平衡点集或线平衡点[23,38,39]. (11)式的特征方程可表示为 表1 典型电路元件参数Table 1 .Typical circuit element parameters. 以表1所列的典型电路元件参数Rc=360 Ω,R=100 Ω为例,此时Rc>R,(2)式有且仅有一个零平衡点S0.由典型电路元件参数,可计算得到零平衡点S0处的五个特征根分别为 不难发现,零平衡点S0处有两个正实根,两个实部为正的共轭复根和一个复实根.说明零平衡点S0是不稳定的,是可以产生混沌吸引子的. 本节固定表1所列的典型参数不变,仅改变电路的初始状态,对电路在不同初始状态下的动力学行为进行研究.这里主要考虑一组微小初始状态和一组特殊初始状态.需要说明的是,为了获得这些不同的初始状态,必须用两个特殊的硬件电路来配置,但难以硬件制作.而PSIM仿真软件是一种电子电路仿真软件包,专门用于电力电子和电动驱动仿真,适用于仿真任何电子电路.因此,本节将利用PSIM电路仿真来验证数值仿真结果. 2.3.1 微小初始状态下的数值仿真和PSIM电路仿真 图3 微小初始状态下数值仿真得到的混沌吸引子在四个相平面上的相轨图 (a)在v1-v2平面上;(b)在v0-i2平面上;(c)在i1-v1平面上;(d)在i2-v2平面上Fig.3 .Numerical simulated phase portraits of chaotic attractors under tiny initial states in four phase planes:(a)In the v1-v2plane;(b)in the v0-i2plane;(c)in the i1-v1plane;(d)in the i2-v2plane. 首先考虑一组微小初始状态v0(0)=0 V,v1(0)=0 V,v2(0)=0 V,i1(0)=0.0001 A,i2(0)=0 A.采用MATLAB龙格-库塔ODE45算法对状态方程组(2)式进行求解,可得到五阶压控忆阻蔡氏混沌电路在四个相平面上典型混沌吸引子的相轨图如图3所示.其中,图3(a)—(d)分别为在v1-v2,v0-i2,i1-v1和i2-v2平面上的相轨图.利用Wolf算法[40]计算(11)式所示的雅可比矩阵可得到典型混沌吸引子的五个不同的李雅普诺夫指数,其值分别为:LE1=1.8326×103,LE2=1.2945×102,LE3= −1.2638×103,LE4= −5.2280×103和LE5=−5.6328×104.该结果进一步说明了五阶压控忆阻蔡氏混沌电路在微小初始状态下运行在混沌轨道上. 根据图1所示的五阶压控忆阻蔡氏混沌电路,利用PSIM电路仿真软件,设计出如图4所示的具有微小初始状态的电路仿真模型.其中电路参数和微小初始状态与图3数值仿真所使用的一致.PSIM仿真得到的混沌吸引子在四个相平面上的相轨图如图5所示.对比分析图3所示的数值仿真结果和图5所示的PSIM电路仿真结果,不难发现两者是完全一致的,表明该五阶压控忆阻蔡氏混沌电路在微小初始状态下确实是可以产生混沌吸引子的. 2.3.2 特殊初始状态下的数值仿真和PSIM电路仿真 接下来考虑一组特殊初始状态v0(0)=0 V,v1(0)= 0 V,v2(0)= 0 V,i1(0)= 0.5 A,i2(0)=0 A.在特殊初始状态下,利用龙格-库塔ODE45算法数值仿真得到的五阶压控忆阻蔡氏混沌电路的周期极限环相轨图如图6所示.其中,图6(a)—(d)分别为在v1-v2,v0-i2,i1-v1和i2-v2平面上的相轨图.同样地,利用Wolf算法[40]计算(11)式所示的雅可比矩阵可得到周期极限环的五个李雅普诺夫指数分别为:LE1=−3.1502×102,LE2= −5.3146×103,LE3= −1.2301×104,LE4= −1.7296×104和LE5= −8.9881×104,进一步证明了五阶压控忆阻蔡氏混沌电路在特殊初始状态下处于周期状态. 图4 具有微小初始状态的PSIM电路仿真模型Fig.4 .PSIM circuit simulated model with tiny initial states. 图5 微小初始状态下PSIM电路仿真得到的混沌吸引子在四个相平面上的相轨图 (a)在v1-v2平面上;(b)在v0-i2平面上;(c)在i1-v1平面上;(d)在i2-v2平面上Fig.5 .PSIM circuit simulated phase portraits of chaotic attractors under tiny initial states in four phase planes:(a)In the v1-v2plane;(b)in the v0-i2plane;(c)in the i1-v1plane;(d)in the i2-v2plane. 图6 特殊初始状态下数值仿真得到的周期极限环在四个相平面上的相轨图 (a)在v1-v2平面上;(b)在v0-i2平面上;(c)在i1-v1平面上;(d)在i2-v2平面上Fig.6 .Numerical simulated phase portraits of periodic limit cycles under special initial states in four phase planes:(a)In the v1-v2plane;(b)in the v0-i2plane;(c)in the i1-v1plane;(d)in the i2-v2plane. 图7 特殊初始状态下PSIM电路仿真得到的周期极限环在四个相平面上的相轨图 (a)在v1-v2平面上;(b)在v0-i2平面上;(c)在i1-v1平面上;(d)在i2-v2平面上Fig.7 .PSIM circuit simulated phase portraits of periodic limit cycles under special initial states in four phase planes:(a)In the v1-v2plane;(b)in the v0-i2plane;(c)in the i1-v1plane;(d)in the i2-v2plane. 选用图6数值仿真所使用的电路参数和特殊初始状态,利用图4所示的PSIM电路仿真模型对其进行电路仿真.此时,PSIM仿真得到的周期极限环在四个相平面上的相轨图如图7所示.显然,PSIM电路仿真结果很好地验证了数值仿真结果. 对比分析上述不同初始状态下的数值仿真结果和对应的PSIM电路仿真结果可知:五阶压控忆阻蔡氏混沌电路在固定电路元件参数不变仅改变电路初始状态的情况下,明显地可观察到电路的运行轨迹因初始状态的不同而出现了混沌、周期两种不同的动力学行为,呈现出混沌吸引子和周期极限环共存的现象,说明该电路在相同的电路元件参数下能够表现出两种不同的稳定状态. 对五阶压控忆阻蔡氏混沌电路中各电路变量和电路参数进行无量纲处理,令 则状态方程组(2)式可改写为 (16)式描述了一个五阶压控忆阻蔡氏系统,该系统有五个系统变量x,y,z,u,w和六个系统控制参数a,b,c,d,e,f.结合表1所列的典型电路元件参数,由(15)式可计算得到六个系统控制参数的典型值分别为a=0.22,b=0.55,c=0.28,d=4.68,e=0.022,f=0.018.进一步对该忆阻蔡氏系统依赖于初始条件的复杂动力学进行了研究. 显然,(16)式有三个确定的平衡点,分别为一个零平衡点和两个非零平衡点,可表示为 (16)式在平衡点¯P=(¯x,¯y,¯z,¯u,¯w)处的雅可比矩阵可表示为 (18)式的特征方程可表示为 (19)式所描述的五次多项式的系数可表示为 以(15)式计算得到的典型系统参数为例,此时c<1,系统(16)式有且仅有一个零平衡点. 对于零平衡点,有¯x=¯y=0,则(20)式可改写为 由(21)式表示的五次多项式的系数不满足劳斯-霍维茨准则[25],说明零平衡点是不稳定的.进一步通过数值计算,得出零平衡点处的五个特征根分别为 此结果说明了零平衡点P0是一个不稳定的鞍点. 将系统参数设定为典型系统参数,并设置初始条件为(x0,y0,z0,u0,w0).固定x0=0,y0=0,z0=0,w0=0不变,选取初始条件u0为分岔参数,u0在[0,0.5]范围内变化时,系统变量y的分岔图如图8所示,该分岔图可以直观地反映出系统在不同初始条件下的动力学行为.对五阶压控忆阻蔡氏系统依赖于初始条件的动力学行为的揭示,有利于深入地研究该系统的双稳定性特性. 观察图8所示的分岔图,可以明显地看出:五阶压控忆阻蔡氏系统在初始条件u0=0.22处产生了混沌危机行为.当初始条件u0在(0,0.22]范围内变化时,五阶压控忆阻蔡氏系统处在不稳定的混沌状态;当初始条件u0在[0.23,0.5]范围内变化时,系统从一开始不稳定的混沌状态经过混沌危机直接进入稳定的周期状态.说明该系统在不同的初始条件下或是混沌的,或是周期的,表现出与初始条件相关的混沌和周期两种不同的动力学行为,呈现出混沌吸引子与周期极限环共存的现象,致使双稳定性现象的产生.对应的MATLAB数值仿真得到的在四个不同平面上的相轨图如图9所示.其中,红色表示从初始条件(0,0,0,0.2,0)出发的混沌运行轨迹,对应的五个李雅普诺夫指数分别为LE1=0.0073,LE2=−2.8476×10−5,LE3= −0.0024,LE4= −0.0159和LE5=−0.1251.蓝色曲线表示从初始条件(0,0,0,0.4,0)出发的周期运行轨迹,对应的五个李雅普诺夫指数分别为LE1=2.4883×10−5,LE2=−0.0117,LE3=−0.0279,LE4=−0.0279和LE5=−0.1640.图9结果表明,该系统在相空间中有着相互独立的混沌吸引盆和周期吸引盆,从相空间中不同初始位置出发的运行轨迹可能被吸引到这两个不同的吸引盆中,导致两种完全不同的稳定状态.这与图8展示的两种动力学行为是一致的. 图8 随初始条件u0变化的系统变量y的分岔图Fig.8 .Bifurcation diagram of system variable y with the variations of initial condition u0. 图9 数值仿真得到的共存混沌吸引子与周期极限环在不同相平面上的相轨图 (a)在x-z平面上;(b)在x-u平面上;(c)在y-w平面上;(d)在u-z平面上Fig.9 .Numerical simulated phase portraits of coexisting chaotic attractor and periodic limit cycle in dif f erent phase planes:(a)In the x-z plane;(b)in the x-u plane;(c)in the y-w plane;(d)in the u-z plane. 为了进一步阐述五阶压控忆阻蔡氏系统的双稳定性特性,固定初始条件x0=0,y0=0,z0=0不变,u0和w0分别在[0,3]范围内变化,绘制出两种具有不同初始条件的共存吸引子在w0-u0平面上的吸引盆如图10所示.其中,红色和蓝色标注的区域分别代表不同类型的吸引子.红色区域代表混沌吸引子,蓝色区域代表周期极限环.值得注意的是,为了对比验证图8分岔图和图9相轨图揭示的双稳定性现象,此处仅对初始条件w0=0时图10吸引盆所刻画的动力学行为进行研究.不难发现,当w0=0时,u0在(0,0.22]范围内处在吸引盆的红色区域,此时系统表现为混沌状态;同样地,u0在[0.23,0.5]范围内对应吸引盆的蓝色区域,系统表现为周期状态.该结果充分论证了图8、图9和图10所表征的动力学行为是十分符合的,说明系统(16)式是一个对初始条件敏感的系统,能够呈现出混沌吸引子与周期极限环共存的双稳定性现象. 图10 初始条件x0=0,y0=0,z0=0时在w0-u0平面上的吸引盆Fig.10 .Attraction basin in the w0-u0plane when initial conditions x0=0,y0=0,z0=0. 本文构建了一个新颖的五阶压控忆阻蔡氏混沌电路,建立了该忆阻电路的数学模型.通过对数学模型的理论分析,发现所构建的五阶压控忆阻蔡氏混沌电路的平衡点随电路元件参数的演化是由一个零平衡点和两个非零平衡点逐渐转变为仅有一个零平衡点,这与常规的忆阻混沌电路所具有的平衡点集或线平衡点不同.采用数值仿真研究了微小初始状态和特殊初始状态下的动力学行为,进而发现了双稳定性现象.搭建了PSIM电路仿真模型,利用PSIM电路仿真很好地证实了数值仿真结果,说明了理论分析的正确性. 为了更好地阐述复杂动力学特性,建立了无量纲系统方程,由此在典型系统参数下讨论了系统的平衡点和稳定性,并利用分岔图、李雅普诺夫指数、相轨图和吸引盆进一步深入研究了系统依赖于初始条件的动力学行为.研究结果表明该系统在给定系统参数下只有一个不稳定的零平衡点,却形成了混沌与周期的非对称吸引子共存的吸引盆,导致混沌吸引子与周期极限环共存的现象产生,意味着系统具有双稳定性特性.此外,迄今为止,鲜有文献涉及忆阻电路的双稳定性研究.而本文所构建的忆阻电路不仅能够产生双稳定性现象,而且所产生的双稳定性现象还与文献[32]中报道的不同,是共存的混沌吸引子与周期极限环.这种特殊的发现具有重要的参考价值和理论指导意义,能够有效地促进忆阻电路基础理论的发展和完善,对推动忆阻电路在信息科学与计算机神经科学等领域的工程应用有着积极的影响.

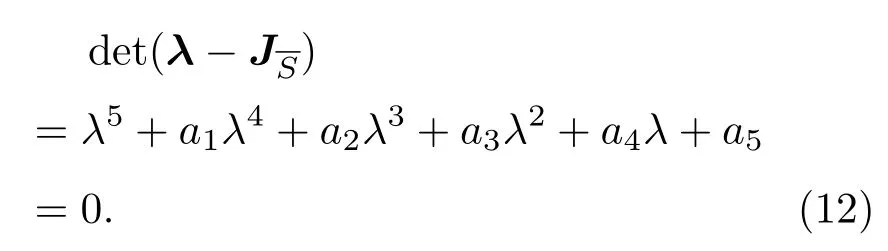



2.3 依赖于初始状态的动力学行为


3 归一化五阶压控忆阻蔡氏系统与双稳定性
3.1 系统的平衡点与稳定性
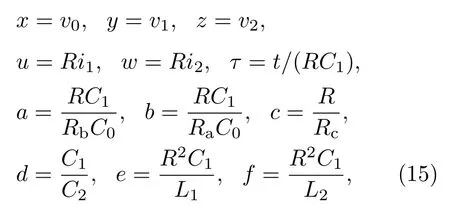







3.2 依赖于初始条件的双稳定性
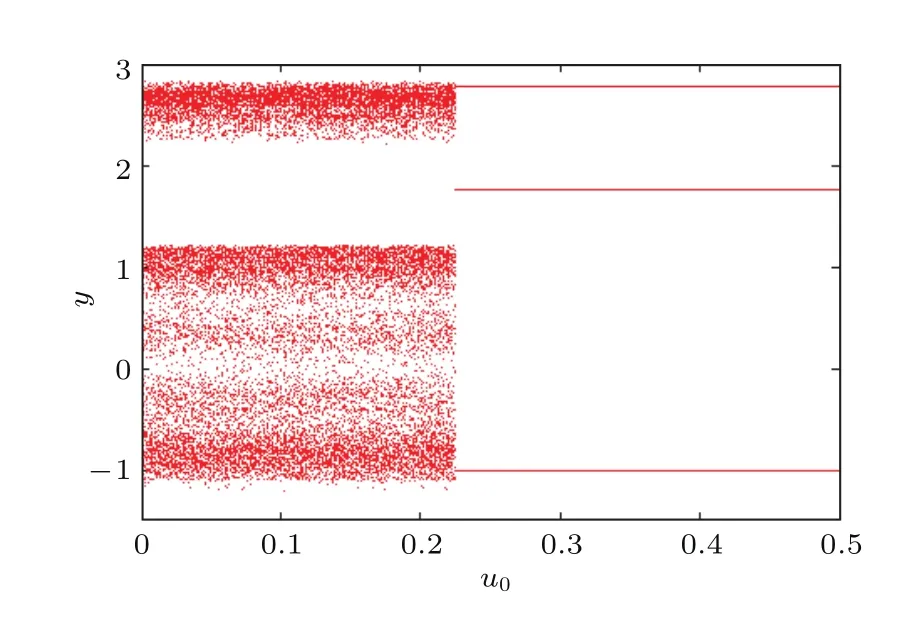

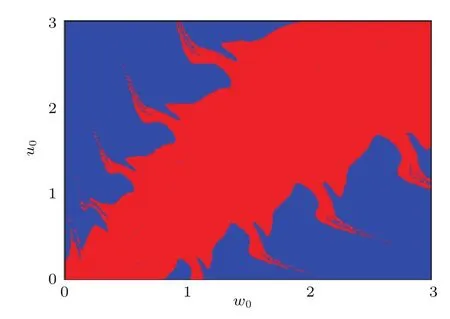
4 结 论

