二维有机拓扑绝缘体的研究进展∗

高艺璇1)3) 张礼智1) 张余洋1)2)3) 杜世萱1)2)3)†

1)(中国科学院物理研究所,纳米物理与器件实验室,北京 100190)

2)(中国科学院物理研究所,松山湖材料实验室,东莞 523808)

3)(中国科学院大学,中国科学院拓扑量子计算卓越创新中心,真空物理重点实验室,北京100049)

(2018年9月14日收到;2018年10月16日收到修改稿)

1 引 言

二维拓扑绝缘体也被称为量子自旋霍尔绝缘体[1],与整数量子霍尔效应息息相关[2,3].二维拓扑绝缘体在带隙中存在具有自旋选择功能的边界态[4−7],这些边界态受拓扑保护而不受弹性背散射和局域化的限制,在自旋电子学和量子计算机等领域有着广阔的应用前景.迄今为止,人们已经在HgTe/CdTe和InAs/GaSb/AlSb两类超晶格材料体系中实现了量子自旋霍尔效应[8,9].随后,科学家预测Bi双层[10−14]和锕基双层化合物[15]是新的二维和三维拓扑绝缘体.最近,基于半导体表面的Bi单层二维拓扑绝缘体的理论预言[16,17]也被实验证实[18].然而这些拓扑绝缘体都是无机材料.与无机材料相比,有机材料具有成本低,易于制造和机械弹性性能好等诸多优点,同时有机材料和基于有机材料的器件也可以实现许多传统的无机材料和基于无机材料的器件具有的物性,例如有机超导[19]、有机发光二极管[20]和有机场效应晶体管[21]等.有趣的是,最近有理论工作预测金属有机晶格中也存在二维拓扑绝缘体[22−25].与二维无机拓扑绝缘体的性质类似,二维有机拓扑绝缘体同样存在自旋轨道耦合导致的带隙和连接价带和导带的拓扑边界态.由于二维无机拓扑绝缘体的种类受到晶体对称性和原子轨道的限制,数量有限.对于二维金属有机材料,由于有机分子的种类丰富,有机分子与金属原子的配位多样,使得可能存在更多二维有机拓扑绝缘体.二维有机拓扑绝缘体的研究进一步扩展了有机材料在自旋电子学中的应用,激发了科学家们的兴趣.随着合成化学和纳米技术的不断发展,科学家们预言并制备了越来越多的二维有机拓扑绝缘体[22−34].

图1 两类二维有机拓扑绝缘体结构示意 (a)六角对称的金属有机晶格;(b)Kagome金属有机晶格Fig.1 . of the two types of organic topological insulators:(a)Hexagonal metal-organic lattice;(b)Kagome metal-organic lattice.

迄今为止,二维有机拓扑绝缘体可以归结为两类.第一类具有六角对称结构,在这类材料中,金属原子组成六角对称结构并与相邻三个分子成键[22−24],如图1(a)所示.第二类具有Kagome结构[25−27,35−38],在这类材料中,金属原子组成Kagome结构,并与相邻的两个分子成键[25−27],如图1(b)所示.本文按照有机拓扑绝缘体的发展历程,对这两类有机拓扑绝缘体的代表工作及最新研究进展进行了介绍.

2 六角对称的金属有机晶格

2013年,Liu团队[22−25]首次从理论上预言了由金属有机晶格构成的六角对称的二维有机拓扑绝缘体.他们以三苯基金属化合物作为基本单元,每个金属原子对称地与三个苯环相连,在三重旋转对称性下倾向于自组装成六角晶格.利用具有强自旋轨道耦合的重金属原子Pb组成Pb(C6H5)3晶格,如图2(a)所示.由于Pb原子具有6s26p2的电子结构且倾向于sp3杂化,平面内的Pb原子分别向苯环平面的上下方向移动造成结构的翘曲,如图2(a)的侧视图所示.计算得到的晶格常数为12.36 Å (1 Å =0.1 nm),Pb—Pb的距离(l)和高度差(h)分别为7.46 Å和2.18 Å.不考虑自旋轨道耦合时,金属有机晶格的能带结构在K点存在一个狄拉克点,费米能级恰好位于狄拉克点处,如图2(b)和图2(c)所示,图2(b)中虚线代表费米能级,插图是材料的第一布里渊区.考虑自旋轨道耦合后,在K点处会打开8.6 meV的能隙,如图2(f)和图2(g)所示.利用第一性原理计算的结果可以拟合得到以最大局域化的万尼尔(Wannier)函数为基础的紧束缚哈密顿量[39].利用这些最大局域万尼尔函数,可以构建半无限拓扑绝缘体晶格的格林函数[40],并计算出边界的局域态密度.图2(d)为由万尼尔函数和第一性原理计算所得的能带结果,两者符合得非常好.从图2(e)中给出的边界局域态密度可以看出(L为原胞沿着边界的长度),非平庸的拓扑边界态连接价带和导带,证明了这种有机材料是二维拓扑绝缘体.

Pb(C6H5)3晶格的拓扑性质可以由K(K′)点附近的物理性质来决定,因此可以用有效哈密顿量来刻画它的低能性质: Hη=}νF(kxτx− ηkyτy)+ ητzh11+ ε0I, 其 中h11=−λSOσz− aλR(kyσx−kxσy),η= ±1分别对应K点和K′点,σ(τ)为自旋(子晶格)的泡利矩阵,νF为费米速度,ε0为格点能量,I为4×4的单位矩阵,λSO为有效自旋轨道耦合,λR为Rashba自旋轨道耦合强度,a为晶格常数.通过拟合第一性原理的结果,得到的拟合参量分别是ε0=0 eV,}νF=1.13 eV·Å, λSO=0.0043 eV,aλR=0.316 eV·Å.在模型中有一项非零的Rashba自旋轨道耦合,这一非零项在平面的石墨烯结构中并不存在,在这里是由于结构的翘曲造成的.结构的翘曲使原胞中的两个金属原子在不同的平面上,导致既有平面内又有平面外的自旋轨道耦合[41].平面内的自旋轨道耦合与石墨烯一样,导致了能隙的打开;而平面外的自旋轨道耦合(石墨烯中不存在),使得z方向存在势能梯度[41],对狄拉克点处的能量色散关系有微小的改变,但对拓扑性质没有影响.用Bi原子替代Pb,可以得到与Pb(C6H5)3相似的拓扑性质,并且存在更大的带隙(43 meV).此外,这类拓扑有机晶格对应力很不敏感,施加±10%的应力时,仍然保持着非平庸的拓扑性质.如果利用过渡金属元素(例如Mn)替换Pb,还可以进一步得到量子反常霍尔绝缘体[23].

金属有机化学和基底调制的分子自组装是合成二维共价有机结构的成熟方法.最近,研究者成功合成出了由金属—碳和碳—碳等有机化学键组成的定向二维共价有机物[42−48].这一突破为合成此类有机拓扑结构提供了可能,在未来的实验中极有可能合成出高质量、大尺寸的此类薄膜材料.

图2 六角对称的二维金属有机晶格Pb(C6H5)3的原子结构和电子性质[22] (a)二维Pb(C6H5)3原子结构顶视图与侧视图,虚线表示单位原胞,l和h表示原胞中两个金属原子的距离和高度差;(b)不考虑自旋轨道耦合时的Pb(C6H5)3晶格的能带结构,虚线代表费米能级,插图是材料的第一布里渊区;(c)不考虑自旋轨道耦合时狄拉克点附近能带结构的放大图,红点是用有效哈密顿量拟合的能带,实线是第一性原理计算的能带;(d)第一性原理和万尼尔能带结构在狄拉克锥附近的比较;(e)半无限晶格的锯齿形边界处的局域态密度,L是原胞沿着边界的长度;(f)考虑自旋轨道耦合之后的Pb(C6H5)3晶格的能带结构;(g)狄拉克点附近能带结构的放大图[22]Fig.2 .Atomic structure and electronic properties of monolayer Pb(C6H5)3in a hexagonal metal-organic lattice[22]:(a)Top and side views of the 2D metal-organic superlattice;(b),(f)band structures of metal-organic lattice without and with spin-orbit coupling(SOC),respectively,the dashed line indicates the Fermi level.The inset shows the f i rst Brillouin zone,and Γ,K,M and K′are the high symmetric k-points;(c),(g)zoom-in band structures around the Dirac point without and with SOC,respectively,the red dots are the f i tted bands using the ef f ective Hamiltonian,and black lines are the f i rst-principles band structures;(d)band structures calculated by f i rst-principles and Wannier functions around the Dirac-cone;(e)energy and momentum-dependent local density of state of the zigzag edge of the semi-inf i nite lattice,L is the unit cell length along the edge.

3 Kagome金属有机晶格

除了前文提到的具有六角对称的二维有机拓扑绝缘体,人们也在尝试设计并在实验中寻找具有新型结构的有机拓扑材料.经过不断的尝试,Wang等[25]发现了具有Kagome晶格的第二类二维有机拓扑绝缘体.在这类材料中金属原子组成Kagome晶格,并与相邻的两个分子成键[25−27,35−38].而由Kambe团队[35]在实验上合成出来的Ni3C12S12金属有机晶格(图3(a))就具有Kagome结构,属于第二类二维有机拓扑绝缘体.

图3(a)展示了二维Ni3C12S12的晶格结构,虚线和实线分别代表Kagome晶格和单位原胞,计算得到的晶格常数是14.63 Å,与实验上的14—15 Å[35]符合得很好.通过第一性原理计算可进一步得到Ni3C12S12的能带结构.考虑自旋轨道耦合效应之后,可以清晰分辨出在费米能级附近存在三条典型的Kagome能带:一条平带,两条狄拉克带,如图3(c)红色线条所示(所有的能带都是自旋退简并的).图3(d)是图3(c)中Kagome能带的放大图,狄拉克点附近的带隙∆1=13.6 meV,平带和狄拉克顶的带隙∆2=5.8 meV.存在拓扑边界态是二维拓扑绝缘体的重要判据,从边界局域态密度(图3(b))可以清楚地看到与体带边缘连接的非平庸的拓扑边界态.

在Kagome晶格上使用单轨道紧束缚模型[49]来描述晶格的电子态特性,相应的哈密顿量在倒空间可以写成如下形式:

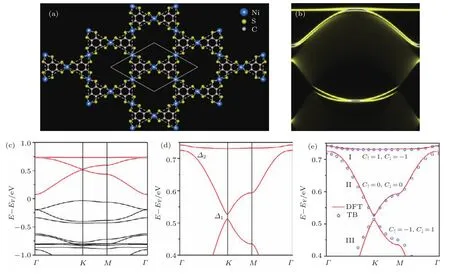
图3 二维Kagome金属有机晶格Ni3C12S12的结构和电子性质[25] (a)结构顶视图,虚线和实线分别代表Kagome晶格和单位原胞;(b)自旋轨道耦合带隙内的半无限狄拉克边界态(包含自旋向上和自旋向下);(c)沿高对称方向的能带结构(考虑了自旋轨道耦合);(d)Kagome能带在两个自旋轨道耦合带隙附近的放大图;(e)第一性原理和单轨道紧束缚计算获得的两个自旋轨道耦合带隙(∆1和∆2)附近的能带结构对比Fig.3 .Atomic structure and electronic properties of monolayer Ni3C12S12in a Kagome metal-organic lattice[25]:(a)A top view of the atomic structure,the solid and dashed lines show the unit cell and the Kagome lattice,respectively;(b)semi-inf i nite edge states(both spin up and spin down components)within the SOC gaps;(c)band structure along the high symmetric directions;(d)zoom-in Kagome bands around two SOC gaps;(e)comparison between f i rst-principles and single-orbital tight-binding(TB)band structures for the f l at and Dirac bands(∆1and ∆2).

为了确认Ni3C12S12晶格的能带拓扑性质,利用Kube公式[50,51]分别计算了具有不同自旋的能带陈数(C=C↑+C↓)和自旋陈数[Cs=对于在费米能级附近的三条Kagome能带,平带和底部狄拉克带具有非零的陈数(±1),而顶部狄拉克带的陈数为零,标在图3(e)中.因此,在自旋轨道耦合带隙(∆1和∆2)内,陈数为0,而自旋陈数为−1,这表明Ni3C12S12薄膜具有非平庸的拓扑性质.

由于过渡金属原子非常容易与分子的硫原子(或者是氧原子)形成配位键,这一类含硫元素的二维金属有机共价材料很容易合成[35−38].此外,通过替换不同的分子与金属原子,不仅可以调节材料的带隙[26,30],还可以得到磁性有机拓扑绝缘体,实现量子反常霍尔效应[34].

4 本征二维有机拓扑绝缘体——Cu-DCA(dicyanoanthracene)分子薄膜

迄今为止,实验合成的第二类有机拓扑绝缘体都不具有本征拓扑性[25−27,35−38,52],在进行拓扑特性测量之前,需要通过电子或者空穴掺杂,将费米能级调控到自旋轨道耦合带隙中[25−27].作为配位聚合物材料,金属有机晶格通常是根据配位化学的特定电子计数规则形成的.不改变几何结构的非等价掺杂很困难,例如用不同价态的外来金属原子代替主体金属原子等,会改变材料的配位化学性质.对于重掺杂情况,可能所有的主体金属原子都要被替换,直到化学计量极限[53].金属有机晶格的掺杂可以通过氧化还原改变金属离子氧化态的方式来实现[54],然而这种方法仍受限于实际可达到的掺杂量.因此,人们仍致力于寻找本征二维有机拓扑绝缘体并实现拓扑态的直接测量.基于对两类有机拓扑晶格的研究,Zhang等[55]发现第一类六角对称晶格最有可能形成本征的有机拓扑绝缘体.通过对大量的实验结构进行金属原子和分子轨道之间的杂化分析,文献[56—58]在现有实验合成的材料Cu-DCA二维有机薄膜中发现了一类本征的二维拓扑绝缘体[55].

9,10-DCA分子含有三个苯环和两个氰基(图4(a)).由于氰基中孤对电子的存在,该分子很容易与一些过渡金属原子形成强配位键.例如,在Cu(111)表面的双层NaCl上可以合成出线性Fe(DCA)2和Ni(DCA)2络合物[59].最近,有两个研究组报道了在Cu(111)表面上生长的Cu-DCA二维薄膜[56,57],如图4(b)所示,白色箭头指向区域边界,插图是高分辨扫描隧道显微镜(STM)图像[57].为了削弱分子薄膜与金属衬底之间的相互作用,有研究组已经在外延石墨烯衬底上合成出了Co-DCA金属有机结构[58],如图4(c)所示.图4(a)给出了Cu-DCA薄膜原子结构,其中Cu原子构成了六角(蜂窝状)晶格(红色虚线),而DCA分子构成了Kagome晶格(蓝色虚线)[49].每个Cu原子与来自DCA分子的三个氰基成键,形成非常强的配位键(Cu—N键长度约为1.88 Å).在每个晶胞中,有两个Cu原子和三个DCA分子.计算得到的Cu-DCA薄膜的晶格常数为20.36 Å,与实验结果(20.8 ű0.2 Å)非常一致[57].仅考虑这类材料的几何结构,它们属于第一类二维有机拓扑绝缘体,即金属原子以六角晶格排列.

图4(d)显示了Cu-DCA薄膜的能带结构和投影态密度,可以看到费米能级附近的典型的Kagome能带特征[36,49,60],Kagome能带由两个狄拉克能带和一个带宽为3.0 meV的平带组成.根据投影态密度,所有的Kagome能带主要来自DCA分子的pz轨道,从Kagome能带对应的局域电荷密度分布图(图4(d)右上角插图)中也能得出相同的结论.最重要的是,与之前人们所研究的Kagome系统不同[25−27,35−38],这一系统费米能级恰好位于狄拉克点处.图4(d)底部两个插图分别表示忽略和考虑自旋轨道耦合的能带.在考虑自旋轨道耦合之后,狄拉克点附近有带隙(∆1=2.9 meV)打开,使得费米能级正好位于自旋轨道耦合带隙内,表明与自旋轨道耦合相关联的固有的拓扑态是本征的.

图4 二维Cu-DCA金属有机晶格的原子结构和电子性质 (a)二维Cu-DCA结构的顶视图,左上角插图是DCA分子结构示意图,红色虚线、蓝色虚线和黑线分别代表Cu原子的蜂窝状晶格,DCA分子的Kagome晶格和单位原胞[55];(b)室温沉积在Cu(111)表面上的Cu-DCA自组装结构的STM图像,白色箭头指向区域边界,插图是高分辨STM图[57];(c)在Gr/Ir(111)表面上Co2(DCA)3金属有机结构的STM图像,左下角的比例尺是1 nm[58];(d)Cu-DCA薄膜的能带结构和投影态密度,其中右上角插图表示费米能级附近的电荷密度分布,底部两个插图分别表示忽略和考虑自旋轨道耦合的能带[55];(e)第一性原理和紧束缚计算的两个自旋轨道耦合带隙(∆1和∆2)附近的能带结构[55];(f)自旋轨道耦合带隙内的半无限狄拉克边界态[55]Fig.4 .Atomic structure and electronic properties of 2D Cu-DCA:(a)Top view of the atomic structure,the inset shows the conf i guration of DCA molecule,the red dashed,blue dashed,and black lines outline the honeycomb lattice of the Cu atoms,the Kagome lattice of the DCA molecules,and the unit cell,respectively[55];(b)STM image of self-assembled structure of DCA on Cu(111)after deposition at room temperature,the white arrows mark a domain boundary,inset is high resolution STM image measured with a DCA modif i ed tip[57];(c)STM topography image of Co2(DCA)3on Gr/Ir(111)surface[58];(d)band structures and PDOS,where the top right inset indicates the charge distribution around the Fermi level,and the bottom two insets show the zoom-in bands without and with SOC,respectively[55];(e)band structures around two SOC gaps(∆1and∆2)calculated by the f i rst-principles and single-orbital TB calculations[55];(f)semi-inf i nite Dirac edge states within the SOC gaps[55].

图4(e)分别利用第一性原理(黑线)和单轨道紧束缚(红点)计算了体系的能带结构,两者之间具有很好的一致性.由于费米能级附近的Kagome能带主要来自DCA分子的pz轨道,因此该分子可以被近似地看作一个超原子.Kagome晶格中的DCA分子之间的电子跃迁由Cu原子连接,从而使得自旋轨道耦合增强,自旋轨道耦合带隙(∆1和∆2)大于纯碳元素材料中的自旋轨道耦合带隙.为了确认Cu-DCA能带的拓扑性质,利用Kube公式分别计算了具有不同自旋的能带陈数(C=C↑+C↓)和自旋陈数对于在费米能级附近的三条Kagome能带,平带和底部狄拉克带具有非零陈数(±1),而顶部狄拉克带的陈数为零,标在图4(e)中.因此,在自旋轨道耦合带隙(∆1和∆2)内,陈数为0,而自旋陈数为−1,这表明Cu-DCA晶格是拓扑非平庸的.从边界的局域态密度,可以清楚地看到与体带边缘连接的非平庸的拓扑边界态,如图4(f)所示.

为了更好地了解Cu-DCA晶格的内在拓扑特性,进一步分析了电子计数和轨道杂化.根据上述计算结果,费米能级附近的Kagome能带主要来自Cu-DCA晶格中DCA分子的pz轨道.即可以将DCA分子视为外壳层中具有两组孤对电子对的超原子,并且倾向于从其最近邻的Cu原子接受电子.Cu原子和DCA分子之间的轨道杂化示意图如图5(a)所示,每个箭头表示具有上或下自旋的一个电子,而每个黑点表示两个自旋简并的电子.Cu原子的d轨道(dxz和dyz)与DCA分子氰基的孤对电子(π轨道)之间的杂化形成四组三重态:成键态t1,t2和反键态 t∗1,t∗2.Cu-DCA 晶格的原胞中共有14个价电子参与轨道杂化,两个来自Cu原子(Cu的其他价电子占据其余d和s轨道不参与杂化),12个来自DCA分子氰基的孤对电子.因此,t1和t2能带被完全占据,另外两个电子填充由t∗1形成的狄拉克带的下半部分,使得费米能级精确地位于忽略自旋轨道耦合的狄拉克点处或者是考虑自旋轨道耦合的带隙中.

图5 二维Cu-DCA的轨道杂化示意图和Au-DCA晶格的电子性质[55](a)Cu原子与DCA分子中氰基的孤对电子对之间的轨道杂化示意图,每个箭头表示自旋向上或向下的一个电子,而每个黑点表示两个自旋简并的电子;(b)考虑自旋轨道耦合后Au-DCA薄膜的能带结构;(c)自旋轨道耦合带隙内的半无限狄拉克边界态Fig.5 . of the orbital hybridization of Cu-DCA lattice and electronic properties of Au-DCA lattice[55]:(a)Orbital hybridization between Cu atoms and the lone pairs from the CN groups of DCA molecule,each arrow denotes one electron with an up or down spin,while each black dot denotes two spin-degenerate electrons;(b)band structure with SOC and(c)the semi-inf i nite edge states within the SOC gaps of Au-DCA.

通过前面电子计数与轨道杂化分析,可以预测具有贵金属与氰基配位的类似结构的二维有机材料也应该是本征拓扑绝缘体.这种金属-氰基的配位结构在金属有机框架中广泛存在.实验上也多次报导过贵金属或过渡金属与氰基有配位作用,例如两重和三重配位的Cu—NC键[56,57,61,62],三重配位的Au—NC键[63],三重和四重配位的Co—NC键[47,64],两重配位的Fe—NC和Ni—NC键[57]等,因此有许多与Cu-DCA晶格相似的结构可以通过多种实验手段进行合成.用Au原子替换Cu-DCA中的Cu原子构成了Au-DCA晶格.在图5(b)和图5(c)中展示了考虑自旋轨道耦合的能带以及非平庸的拓扑边界态.Au-DCA和Cu-DCA晶格的能带结构和拓扑性质都非常相似,并且Au-DCA晶格具有更大的自旋轨道耦合带隙.

5 总结与展望

目前理论上已经预测了一系列的二维有机拓扑绝缘体,但是一般二维有机薄膜均生长在金属衬底上,由于金属有机晶格与金属衬底的相互作用很强,材料的拓扑性质会被基底覆盖,因此减弱金属有机晶格与金属衬底之间的相互作用已成为未来发展的核心问题.本研究领域的另一个挑战是目前合成的二维金属有机材料尺寸太小,一般在纳米尺度,不适合用来测量晶体材料的拓扑性质.值得强调的是2017年11月Liljeroth团队[58]在外延石墨烯衬底上合成出了Co与有机分子配位形成的金属有机结构,削弱了金属衬底对材料内禀属性的影响,为测量材料的拓扑性质提供了一条新的途径.从2013年二维有机拓扑绝缘体发现至今,这类材料还处于研究的初级阶段,进一步的深入研究为实验上合成二维有机拓扑绝缘体以及构建三维有机拓扑绝缘体提供了新的思路.

特别感谢美国犹他大学Feng Liu教授,感谢中国科学院物理研究所陶蕾博士、金鑫和张现利对文章写作的建议.