偶极玻色-爱因斯坦凝聚体在类方势阱中的Bénard-von Kármán涡街∗

席忠红1)2)3) 杨雪滢1)2) 唐娜1)2) 宋琳1)2) 李晓霖1)2) 石玉仁1)2)†

1)(西北师范大学物理与电子工程学院,兰州 730070)

2)(甘肃省原子分子物理与功能材料重点实验室,兰州 730070)

3)(甘肃民族师范学院物理与水电工程系,合作 747000)

(2018年8月28日收到;2018年9月26日收到修改稿)

1 引 言

当玻色-爱因斯坦凝聚体(Bose-Einstein condensate,BEC)体系中存在大量涡旋成核时,这些涡旋的排列方式是一个非常值得研究的物理问题[1,2].俄国物理学家Abrikosov[3]在研究超导理论时最先讨论了量子化的涡旋结构,并提出了Abrikosov三角涡旋晶格,之后其他物理学家在单分量BEC中也发现了Abrikosov三角涡旋晶格[4].然而,随着对此类问题研究的不断深化,研究人员发现,BEC中的涡旋结构不仅仅局限在三角晶格结构[5].实验和理论研究表明,由于BEC系统受到相互作用、外势、多分量、旋转角频率等诸多因素的影响,系统有更加新奇的涡旋结构[1,5].

当经典流体流过障碍物时,一种普遍而有趣的现象是在尾流中交替产生涡旋对,这就是著名的Bénard-von Kármán涡街[6−8].自从实验和理论上发现von Kármán涡街以后,物理学家对其做了大量研究.众所周知,当黏性流体流过障碍物时其行为主要取决于表征流体黏性的雷诺系数Re[6,7],然而,由于超流体无黏性,导致无法定义其黏性系数[9].超流体涡旋的量子化使得其动力学行为与经典流体有很大区别[10],因此在超流体的尾流中能否产生并形成稳定的von Kármán涡街就成为一个有意义的课题.近几年物理学家就该领域做了大量研究,取得了很多成果.Sasaki等[11]通过数值求解Gross-Pitaevskii(GP)方程,成功模拟了无偶极相互作用BEC尾流中出现的稳定von Kármán涡街,给出了其相图.Kwon小组[12−14]从实验上研究了障碍势在稀薄原子气体BEC中运动时尾流中的von Kármán涡街.Sasaki等[15]研究了双组分BEC中分离相的动力学行为,发现在强相分离情形下,组分1的原子在组分2中运动时会分裂成量子化涡旋并在尾流中形成von Kármán涡街.

当超冷原子气体的电偶极或磁偶极的相互作用不可忽略时,须考虑原子间的偶极效应.偶极效应远比各向同性的s波作用复杂得多,是一种长程各向异性的相互作用,会对超冷原子气体的基态相图、稳定性以及动力学行为产生重要影响[15−19].此外,偶极间的各向异性相互作用也提供了一个可控参量,使得偶极凝聚体在量子模拟和计算等许多高水平的研究领域有了应用的可能[20].但据我们所知,偶极BEC中的涡街现象一直未有报道.

本文对偶极BEC在类方势阱中的Bénard-von Kármán涡街现象进行了数值研究.结果表明,当障碍势在BEC中的运动速度与尺寸在适当范围内时,系统中会出现稳定的两列涡旋对阵列,即Bénard-von Kármán涡街.本文也研究了偶极相互作用强弱、障碍势尺寸以及运动速度对尾流中产生的涡旋结构的影响,得到了相图结构,并对障碍势所受拖拽力进行计算,分析了涡旋对产生的力学机理.

2 理论模型

考虑质量为m的偶极原子BEC束缚在势阱Vext中,障碍势VOP在BEC中沿x方向以速度υ运动.设原子沿轴n=(nx,ny,nz)极化,其中在平均场近似下,可以得到描述系统的GP方程[19−22]

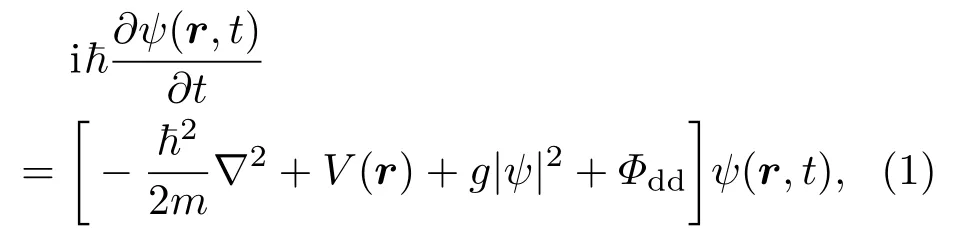
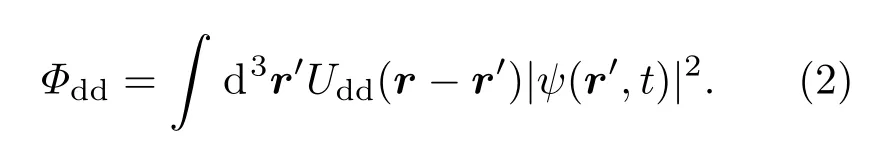
偶极相互作用为

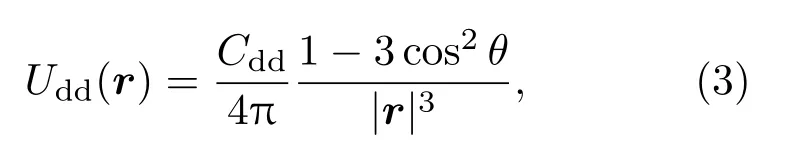
实验中,BEC原子通常被置于谐振子势阱中.若谐振子势频率满足ωz≫ωx,ωy,则BEC将被束缚在xoy平面内.此时,可先进行准2维近似[22],然后进行无量纲化处理:,并略去变量上的”∼”号,其中,ω0= ωx,从而得无量纲化准二维GP方程[25]

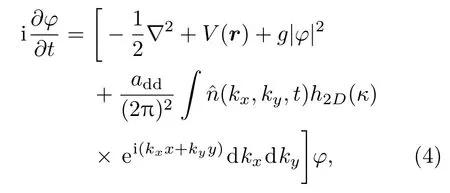
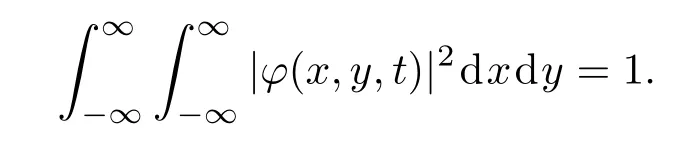
方程(4)中

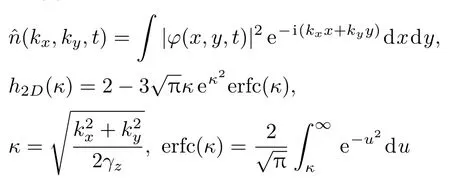
为完全误差函数,γz=ωz/ω0.

数值计算针对方程(4)进行,计算范围取为{(x,y)||x|<512,|y|<128}.用φ=1作为初始波函数,利用虚时演化法[26]得到系统的基态.然后取该基态作为初始条件,利用时间劈裂傅里叶谱方法[27]对GP方程(4)进行非线性动力学演化,从而对系统的动力学行为进行研究.

3 数值结果

考虑外势为下面的类方势阱[28]

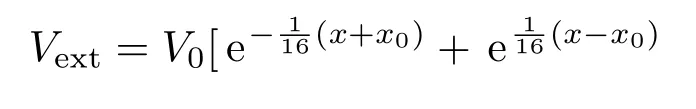
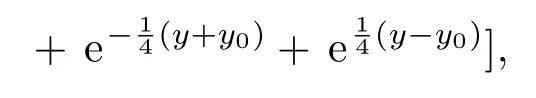
其中V0是无量纲化的外势深度;±x0,±y0分别表示x,y方向上阱壁所在位置.该势阱的特点是在阱壁处势很强而阱内离开阱壁处势很快降为接近于0,故可视为对无限深方势阱的一种近似.当V0=1000时外势形状如图1所示.

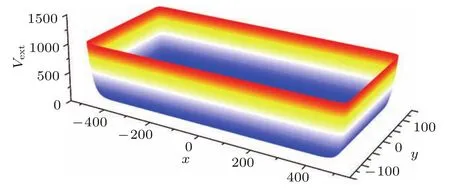
图1 外势形状图 (取外势深度V0=1000,阱壁位置x0=512,y0=128)Fig.1 .Shape of external potential(The depth of external potential is V0=1000,and the position of a potential wall is x0=512,y0=128).

将N=2.5×105个164Dy原子BEC束缚在该势阱中,164Dy原子磁偶极矩为10µB(µB为玻尔磁子),原子质量m=2.72×10−25kg.取谐振子势频率(ωx,ωy,ωz)=2π×(4.3,56,350)Hz,这与Berkeley等团队的实验参数一致[11].由此可得偶极相互作用系数add≈0.2.通过Feshbach共振调节s波散射长度使as≈8.0×10−13m时,由得g≈1.故在计算中取add=0.2,g=1.考虑无量纲化的圆柱形障碍势

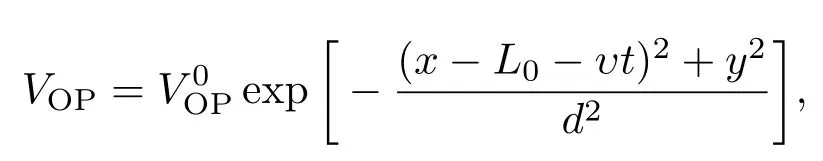
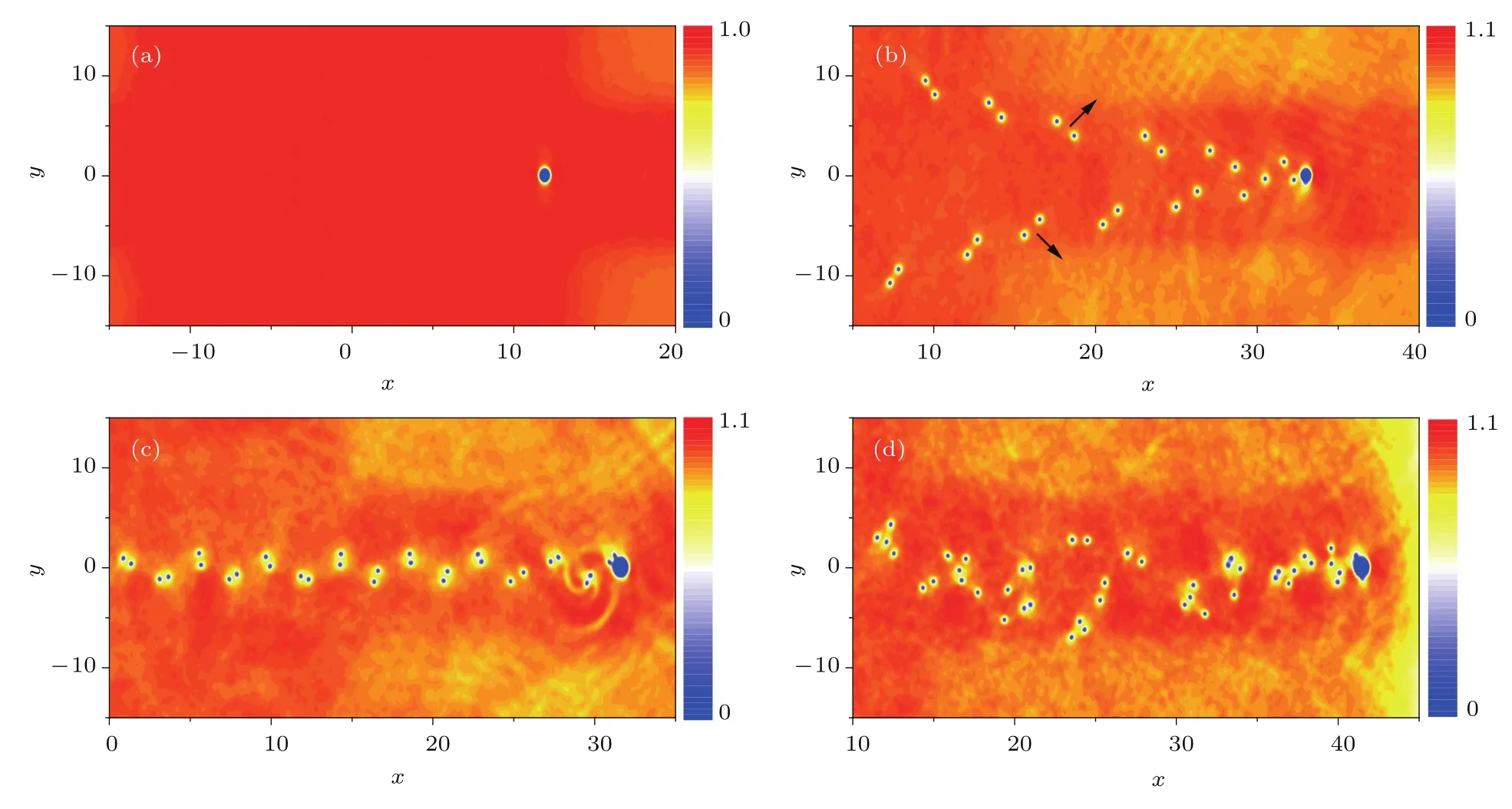
图2 障碍势在偶极BEC中运动时尾流密度分布 (a)υ=0.25,d=1.2;(b)υ=0.49,d=1.2;(c)υ=0.48,d=1.8;(d)υ=0.55,d=1.82Fig.2 .Density distributions of a condensate past an obstacle potential:(a)υ=0.25,d=1.2;(b)υ=0.49,d=1.2;(c)υ=0.48,d=1.8;(d)υ=0.55,d=1.82.

从图2可以看出,当障碍势的运动速度υ足够小时,障碍势周围的凝聚体是稳定的层流形式,没有涡旋产生(图2(a)).当障碍物势的运动速度υ达到某个临界值时,尾流中开始产生如图2(b)所示的涡旋-反涡旋对.这个临界值主要取决于障碍物势的形状和原子之间的相互作用[9].当一对涡旋从障碍势脱落后,附近的凝聚体很快达到产生涡旋的临界条件并产生新的涡旋对,这样就在障碍势后面产生了上下两列涡旋对阵列.由于一个涡旋对中的两个点涡旋有着不同的旋量±h/m(h为普朗克常量),使得两列对称分布的涡旋对阵列不稳定[11].受到小的扰动时,涡旋对会沿着垂直于涡旋对连线的方向(图2(b)黑色箭头所示方向)平动,从而在尾流中形成V字形涡旋对阵列结构.一些学者在研究经典流体时也发现了这种交替的涡旋模式[29−31].这种涡旋结构在υ比较大、d比较小时更加明显,与经典流体中的尾流模式非常类似[11].

当障碍势的运动速度υ增大到一定程度并且障碍物的尺寸d在适当范围内时,其后同时产生的一组涡旋对具有相同的旋量h/m或−h/m,以角频率2~/(md20)绕着它们的中心运动[11],在运动过程中两个点涡旋之间的距离d0基本保持不变.这样,在尾流中交替产生的旋量相反的涡旋对就形成稳定的两列涡旋对阵列,即Bénardvon Kármán涡街(图2(c)). 在图2(c)参数条件下,数值计算得到上下两列涡旋阵列之间的距离b≈19a0,同一阵列中两个涡旋对之间的平均距离ℓ≈68a0,因此b/ℓ≈0.28.该值与经典流体中Bénard-von Kármán涡街产生的稳定性条件以及Sasaki等在研究无偶极相互作用BEC时的结论一致.当障碍势的运动速度υ继续增大时,障碍物势后尾流中的这种周期性涡街消失,在尾流中出现混乱的涡旋结构(图2(d)).

为研究各种尾流结构的参数区间,我们对系统在不同υ和d时的情形进行了大量数值计算(图3为其相图结构).

图3 尾流结构随障碍势尺寸d和运动速度υ的变化Fig.3 .Dependence of the patterns of wakes on the normalized width d and velocity υ of the obstacle potential.

从图3可以看出,沿图中箭头所示方向改变参数时,障碍物势后尾流的结构依次出现稳定的层流、涡旋对、von Kármán涡街以及混乱的涡旋结构,分别与图2(a)—(d)相对应.显然,von Kármán涡街出现的参数范围相对较小,具体约为1.0 6 d 6 3.4,0.37 6 υ 6 0.54.图3与无偶极相互作用时的相图结构也存在较大不同.在无偶极相互作用的BEC中(add=0),d>1.5时,尾流从稳定的层流直接过渡到卡门涡街或者混乱模式,而不会出现图3中较宽范围的涡旋对结构.同时,随着偶极相互作用强度的增加,相图中von Kármán涡街出现的参数区域变得更窄.然而,对于经典流体,在雷诺数Re变化的较大范围内都会出现von Kármán涡街[32−35].

以上数值结果容易在实验中得以实现.考虑将N=2.5±0.5×105个164Dy(磁偶极矩为10µB)或52Cr(磁偶极矩为6µB)或168Er(磁偶极矩为7µB)等原子BEC束缚在方势阱中,取谐振子势频率(ωx,ωy,ωz)=2π × (4.3,56,350)Hz[11]. 此时,偶极相互作用系数add≈0.2.通过Feshbach共振调节s波散射长度使接触相互作用系数g≈1.当尺寸

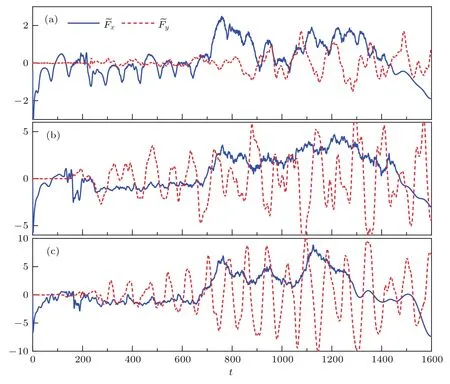
图4 无量纲化拖拽力˜F随时间的变化(a)υ=0.49,d=1.2;(b)υ=0.48,d=1.8;(c)υ=0.55,d=1.8Fig.4 .Time evolution of the normalized drag force˜F:(a)υ=0.49,d=1.2;(b)υ=0.48,d=1.8;(c)υ=0.55,d=1.8.

为1.0a06 d 6 3.4a0的激光束以速度在偶极BEC中运动时,将会在激光束后尾流中周期性产生涡旋对,形成稳定的Bénard-von Kármán涡街.

若考虑将N=2.0±0.5×103个164Dy原子BEC束缚在类方势阱中,通过Feshbach共振调节s波散射长度as=4.08×10−9m ≈ 77aB,aB为玻尔半径.此时接触相互作用系数g≈100,偶极相互作用系数add≈20(其他参数与前面相同),仍有add/g=0.2.数值结果表明,此时也会出现图2(c)中所示的Bénard-von Kármán涡街现象.

4 结 论

对偶极BEC在类方势阱中的Bénard-von Kármán涡街现象进行了研究.在平均场近似下,通过虚时演化法得到系统的基态,然后利用时间劈裂傅里叶谱方法对系统进行非线性动力学演化,发现障碍势在偶极BEC系统中以一定速度运动时,系统中会出现稳定的两列涡旋对阵列,即Bénardvon Kármán涡街;数值研究了偶极相互作用强弱、障碍物势尺寸以及运动速度对尾流中产生的涡旋结构的影响,得到了系统的相图结构;通过对障碍势所受拖拽力进行计算,分析了涡旋对产生的力学机理.