基于频繁模式发现的时间序列异常检测方法

李海林，邬先利

(华侨大学 信息管理系，福建 泉州 362021)(*通信作者电子邮箱1519998683@qq.com)

0 引言

近几年，时间序列的异常研究渐渐兴起，成为时间序列数据挖掘的一个新热点，并被广泛地应用于航天、医疗、网络监测等领域。航路飞行目标的属性异常检测是确保及时发现飞行异常的关键问题，对此，王晓华等[1]通过在时间序列上的指派融合，对比预测值和观测值差异，检测航路目标异常变化。在时间序列的异常检测实际应用中，刘炜等[2]从时间序列角度出发，提出一种基于结构相似度准则的输油管道泄漏检测定位方法。

在时间序列异常研究中，相对于单个序列点的异常，大家更多关心的是序列在一段时间内的异常变化情况[3]。现有的方法有基于扩展符号聚集近似的水文时间序列异常检测方法(Extended Symbolic Aggregate Approximation based anomaly mining of hydrological time series, ESAA)[4]。首先通过基于扩展符号聚集近似(Extended Symbolic Aggregate Approximation, ESAX)方法对时间序列进行重新描述，然后计算某序列与时间序列数据集中其他序列之间的累积距离，以此来衡量其异常程度。时间序列的累积距离越小，其为异常的可能性也就越小。该方法能较好地压缩数据并发现异常，但对于时间序列的异常检测，每增加一条新的序列就需要该序列与数据集中每一条序列作距离测量，如果数据集中的序列过少则不能较好地发现异常；然而，如果数据集中的序列过多则会耗时耗力，特别是对增量式数据，更是不适用。后续研究在此问题上提出基于层级实时记忆算法的时间序列异常检测方法[5]、基于滑动窗口预测的水文时间序列异常检测方法(Time Series Outlier Detection based on sliding window prediction, TSOD)[6]等，通过对时间序列内在模式关系进行学习，建立预测模型，通过比较预测值和真实值的偏离程度来判断数据是否异常。这类方法对含有噪声的数据检测率较低，对数据干扰较为敏感。鉴于传统方法对增量式数据挖掘效率较低等问题，提出基于频繁模式的时间序列异常检测方法。

1 相关理论基础

1.1 符号集合近似

符号集合近似(Symbolic Aggregate Approximation, SAX)[7-8]是由Keogh在分段累积近似(Piecewise Aggregate Approximation, PAA)的基础上提出的一种有效的时间序列数据离散化降维方法,通过将数值转换为离散的符号来对时间序列重新描述，因其简单易用、不依赖于具体实验数据等特点而得到越来越多的关注。

SAX可分为3个步骤。

首先,用Z-score标准化方法对时间序列L={l1,l2,…,li,…,lm}(例如t=(0∶0.001∶2),L=sint)进行预处理，得到均值为0、标准差为1的序列C={c1,c2,…,ci,…,cm}。

(1)

然后,选择合适的压缩阈值w(例：w=1 000),对C进行 PAA表示，得到U={u1,u2,…,un}(例如U={0.65，1.35，0.82，-0.47，-1.33，-0.96，-0.20})其中m是序列L的长度，n为时间序列的PAA表示的长度。

最后,离散化，选定字母集大小即基大小a(例如a=3),根据字母集大小在高斯分布表(如表1)中查找区间的系列分裂点。

表1 基从3到7的分裂点

将PAA表示的均值映射为对应的字母，最终离散化为字符串H={h1,h2,…,hn}(例如H={a,a,a,c,c,c,b})。其主要实现过程如图1所示。

图1 SAX方法实现过程示意图

1.2 频繁模式

频繁模式是频繁地出现在数据集中的模式。如首先购买PC，然后是数码相机，再后是内存卡，如果它频繁地出现在购物历史数据库中，则称它为一个(频繁的)序列模式。频繁模式挖掘是一项数据挖掘任务，它发现频繁出现并且具有某些突出性质的模式，这些性质使它们有别于其他模式，常常揭示某些固有的和有价值的规律。

序列模式挖掘算法[9-10]就是找出序列支持度大于或等于min_sup的所有频繁序列, 其中，min_sup是用户预先指定的最小支持度阈值。假设有序列数据集D={I1,I2,…,Ia}，一般的序列I={k1,k2,…,kp},序列I的支持度support(I)是包含I的所有数据序列所占数据集D的比例。如果序列I的支持度大于或等于用户指定阈值min_sup，则称I是一个频繁序列。

support(I)=P(I∪D)

(2)

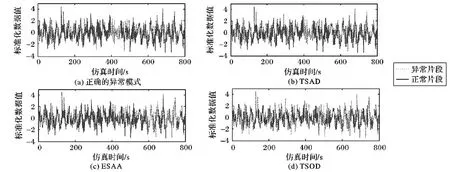
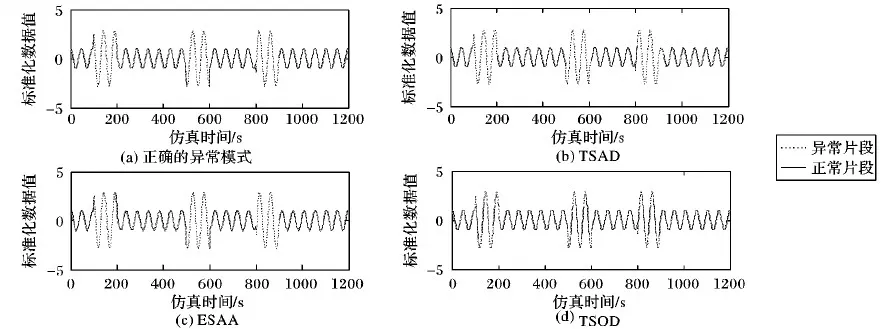
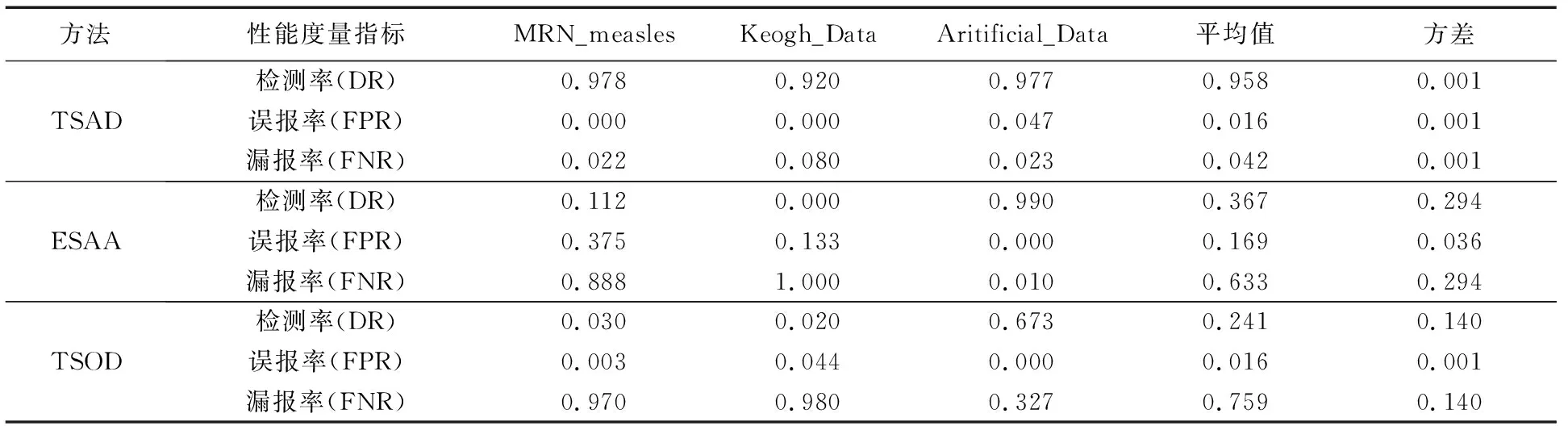
设n维序列P={p1,p2,…,pn},m维序列Q={q1,q2,…,qm}，其中m>n，若序列P中每个元素都在序列Q中相同位置出现，即pi=qi(i

频繁序列挖掘和频繁项集挖掘一样，首先遍历一次序列数据集D，得到所有的频繁1-序列, 按照频繁1-序列把数据集D划分为各个频繁 1-序列作为前缀的投影数据集; 在生成得到的各个投影数据集中继续递归挖掘子频繁序列; 将投影数据集中的序列当作新的序列数据集，按照上述步骤重新扫描并形成频繁序列项，然后挖掘各个频繁项的投影数据集，直到没有新的投影数据集产生，即获得所有的频繁序列。

2 异常序列检测

2.1 频繁模式挖掘

频繁模式的挖掘是本文提出的新方法中的重点，也是比较传统方法的优势所在，因为理论上得到的频繁模式看作正常序列的标准，省去了待测序列与所有序列都作相似性度量的繁杂，只需与该模式作相似性度量即可初步判断其是否为异常序列。

在寻找频繁模式前需对所有序列进行预处理，用SAX方法对时间序列进行重新描述可以在压缩数据的同时保留较多的局部信息，而且分段过程能实现数据的噪声消除，重新描述的数据结果在视觉上表现得简洁直观。

对频繁模式挖掘，主要算法步骤如下。

输入 训练序列，最小支持度min_sup;

输出 频繁序列p。

步骤1 用SAX方法将序列符号化，得到字符序列。

步骤2 首先遍历一次字符序列S，提取序列中每个长度为1的字符存入候选集U(相同字符只提取一次)。

步骤3 查找序列中U中每个序列的个数，计算其支持度。

步骤4 将支持度大于min_sup的1-序列表示为候选频繁序列q，若q为空，则跳到步骤7)；反之，p=q。

步骤5 将p进行自连接得到新的候选集并让其替代U。

步骤6 检测U是否为空，若U为空，则继续步骤7；否则跳到步骤3。

步骤7 输出最终的频繁序列p。

该方法结合了时间序列的频繁序列挖掘和数据挖掘中频繁项集的挖掘思想，不同于这两种思想的是该方法对时间序列不需要进行分段，没有数据项，仅仅用字符序列进行挖掘，省去了序列划分的繁杂过程，也避免了因序列划分不当而引起的某些模式被忽略的情况。方法过程中的支持度是序列模式的个数。该方法至少要遍历序列S一遍，但时间复杂度不高，当min_sup为1且S中所有字符不同时，时间复杂度最高为n2，但这样的挖掘是没有意义的，所以在一般情况下，时间复杂度都会比这个小很多。

2.2 异常检测

目前，时间序列的异常还没有一个公认的定义，普遍采用Hawkin给出的定义[11]：异常是在数据集中偏离大部分数据的数据，使人怀疑这些数据是由不同的机制产生的，而非随机偏差。由此可以想到异常所偏离的大部分数据一定存在一个共同的模式，所以本文要用挖掘出的这一模式作异常检测，便会省去许多繁杂的过程。

同时，为了检测出所测序列的片段异常，本文需要对序列进行分段。滑动窗口分段压缩算法[12]是通过不断利用最小二乘法去拟合当前窗口所有样本点组成的子序列，若拟合误差没有超过预先设置好的阈值，则扩大窗口加入新的样本点到子序列直到窗口到达终点。若子序列的拟合误差超过阈值，则从下一个样本点开始重新划分窗口继续拟合直线。

结合上述方法思想，本文提出的异常检测方法步骤如下：

输入 需检测的时间序列L，滑动窗口分段的拟合误差maxError，频繁模式序列p；

输出 序列L的异常片段G。

步骤1 用滑动窗口对序列L进行分段：

1)初始化第一段子序列的分段点index=1；

2)i=index,判断滑动窗口是否到达终点，如果到达终点，则跳到5)；

3)往滑动窗口中加入新的序列点Li，利用最小二乘法去拟合当前窗口所有样本点组成的子序列；

4)判断拟合误差是否大于阈值maxError，如果小于maxError，则令i=i+1跳到3)；

5)合并该子序列到F，如果滑动窗口没有到达终点，则跳到2)，反之执行步骤2。

步骤2 用SAX将子序列集F符号化，生成符号表示的子序列集H。

步骤3 用最长公共子序列对频繁模式序列p与H作相似性度量，找出H中相似度低的子序列，并将其存入异常序列候选集G。

步骤4 计算异常序列候选集G占序列L的比例，如果比例超过0.5，提示频繁序列已经过期，需挖掘新的频繁模式；否则输出G。

待测序列L的长度为m时，该方法中滑动窗口分段的时间复杂度为m。当maxError最小，即分段结果为每个数据自成一段时，相似性度量的时间复杂度为m，所以该方法的时间复杂度最大为2m。

3 数值实验

3.1 仿真实验

3.1.1 实验数据

对心电图时间序列的异常检测具有重要的医学价值，对于重症患者实行实时的心脏监控也是必要的。本文实验所采用的数据集从 MIT-BIH ECG 数据库[13]中下载。 MIT-BIH 数据库共包含 48 条超过30 min的心电图数据。 图3实验结果所使用的数据是编号为104的时间序列，该序列为一个66岁女性30 min的心电图数据，实验选取了前5 000个数据点做实验。表2给出了该序列的特征点以及相应发生时刻, 其中室性早搏(Premature Ventricular Contractions, PVC)是多样的，几次爆发的肌肉噪声。

表2 实验数据基本信息

3.1.2 实验准备

参数maxError,选择该参数时可观察序列的波形，尽可能地使分段能包含一个周期序列(如图2)，该实验选择的maxError=170；参数min_sup,选择该参数时观察训练序列的波形，大概有几个完整的正常周期就拟订为几，该示例实验选择的min_sup=5(如图2)；w主要是符号化时对序列的压缩，该参数的选择表现的是序列的走向，所以可根据时间序列的具体情况而定，如果序列骤变性较强则不应该选择过大，视具体序列而定，该实验示例选择的w=50；a为字母集大小，该实验示例选择的a=3。

图2 训练数据集

3.1.3 实验过程

用SAX方法把序列R进行符号化得到S={acaabbbcbabbbcabbbcbabbbcbabba}，用时间序列的频繁模式挖掘算法寻找符号序列S中的频繁序列，获得频繁序列p={ab,bb}，用滑动窗口分段对序列L进行分段，得到的子序列在L中的位置为F={1～232,233～539,540～805,806～1 118, 1 119～1 442,1 443～1 645,1 646～2 067,2 068～2 361,2 362～2 651,2 652～2 941,2 942～3 231,3 232～3 513,3 514～3 715,3 716～4 142,4 143～4 423,4 424～4 708,4 709～4 997,4 998～5 000}，再次用SAX方法将子序列集F符号化，生成符号表示的子序列集H={cbaaba}{a} {acaab}{bacbabb}{bbcaab}{bbcbabb}{bbcaabb}{accbb}

{bbbbaabba}{cbabbb}{cbabbb}{ccabcb}{ccabbb}{ccabbb}

{accbb}{babbabbab}{caabba}{caabba}，再用p与H进行相似性度量，找出相似度低的子序列，并将其存入异常序列候选集G={1 442～1 645,3 513～3 715,4 997～5 000}，最后计算异常序列候选集G占序列L的比例为0.166 7，小于0.5，所以输出G。

3.1.4 实验结果及分析

实验结果如图3所示，结合表1对数据的描述可发现，该异常片段为该数据产生者爆发的肌肉噪声，实验结果与数据的描述相符。

图3 异常检测实验结果

3.2 对比实验

为检验基于频繁模式的时间序列异常检测方法的可行性和优越性，在此选择3种性质不同的数据进行异常检测实验，采用余宇峰等[6]提出的基于滑动窗口预测的水文时间序列异

常检测(TSOD)和刘千等[4]提出的基于扩展符号聚集近似的水文时间序列异常挖掘(ESAA)两种方法与本文方法作比较。

3种数据各具代表性:第1种数据MRN_measles数据是真实数据，其中异常的数据明显高于其他数据点; 第2种数据Keogh_Data是仿真数据，其中加入了较多干扰; 第3种数据Aritificial_Data是比较规则的周期数据异常。下面是三种数据的实验结果及分析。

3.2.1 实验结果及分析

实验1 真实数据MRN_measles[14]。该数据是长度为534的时间序列，在区间[150，170]和[420，534]存在异常情况，如图4(a)所示。通过TSAD方法对该序列进行异常检测，实验的相关参数分别设置为滑动窗口最大误差maxError=25，符号化压缩阈值w=10，最小支持度min_sup=15。检测出的异常片段为[152,166]、[417,534]，实验结果如图4(b)所示；通过ESAA方法对该序列进行异常检测，检测出的异常片段为 [151,165]、[181,195],实验结果如图4(c)所示。通过TSOD方法对该序列进行异常检测，检测出的异常片段为[158,162]、[195,196]，实验结果如图4(d)所示。

图4 三种方法对MRN_measles数据实验结果

图4中虚线画出的序列为检测出的异常片段，可以看出，TSAD能很好地检测出原序列的两个异常片段；ESAA只能较好的检测原序列中凸起的一个片段异常，而未能检测出序列中平滑的片段异常，同时还误将片段[181,195]认为异常；TSOD方法虽然也检测出来凸起的片段异常，但没能准确地测出该段的所有异常，同时也误将一个正常片段当作异常。比较三种方法对数据MRN_measles的检测效果可以看出，TSAD方法检测效果最好，其次是ESAA方法，TSOD方法检测效果最差。

实验2 Keogh_Data数据是Keogh等[15]进行时间序列异常检测时使用的仿真数据，由以下随机过程产生:

(3)

(4)

其中:t=1,2，…，N, 实验取值为N=800，即实验仿真得到长度为800的序列；自定义n(t)是均值为0，标准差为1的加性高斯噪声；e(t)为自定义的异常事件，具体如下:

(5)

通过TSAD对序列L2(t)进行异常检测，实验的相关参数分别设置为滑动窗口最大误差maxError=27，符号化压缩阈值w=3，最小支持度min_sup=35。检测出的异常片段为[402,448]，实验结果如图5(b)所示。通过ESAA方法对该序列进行异常检测，检测出的异常片段为[601, 650]、[701,750]，实验结果如图5(c)所示。通过TSOD方法对该序列进行异常检测,检测出的异常片段为[55,56]、[68,69]、[91,92]、[115,116]、[129,139]、[140,141]、[232,233]、[235,236]、[246,247]、[255,256]、[269,270]、[290,291]、[320,321]、[344,345]、[393,394]、[396,397]、[419,420]、[472,473]、[485,486]、[498,499]、[504,505]、[519,522]、[597,598]、[614,615]、[630,631]、[640,641]、[650,651]、[679,680]、[695,696]、[727,728]、[743,744]、[746,747]、[793,794]，实验结果图5(d)所示。

由图5可以看出：TSAD方法正确地检测出了原序列中的大部分异常，仅仅漏掉少有的个别异常点；而ESAA方法检测到两段异常片段，但没能检测出真正的异常片段，该方法对这种数据的检测效果非常不理想；TSOD方法虽然检测出了真正异常片段中的几个小片段，但也将一些正常片段看作异常测出，误报率也是较大，由此可以看出TSOD和ESAA两种方法对Keogh_Data数据的检测效果非常差。

实验3 Aritificial_Data数据[16]，时间序列由如下随机过程产生：

(6)

(7)

其中t=1,2,…,N,实验取值为N=1 200，即实验仿真得到长度为1 200的序列。序列L1(t)没有异常，将时间序列L1(t)加上异常事件e(t),即变形为包含异常序列的时间序列L2(t)。异常事件e(t)定义如下：

e(t)=

(8)

通过TSAD方法对序列L2(t)进行异常检测，实验的相关参数分别设置为滑动窗口最大误差maxError=48，符号化压缩阈值w=7，最小支持度min_sup=20。检测出的异常片段为[94,203]、[499,609]、[807,923]，实验结果如图6(b)所示。通过ESAA方法对该序列进行异常检测，检测出的异常片段为[101,200]、[501,600]、 [801,900]，实验结果如图6(c)所示。通过TSOD方法对该序列进行异常检测，检测出的异常片段为[100,102]、[115,127]、[139,151]、[161,177]、[185,200]、[500,557]、[569,581]、[594,600]、[800,846]、[857,869]、[881,893]，实验结果如图6(d)所示。

由图6(a)和图6(b)对比可以看出，TSAD方法能较好地测出原序列中存在的异常；对比图6(a)和图6(c)可以看出，ESAA方法能非常准确地检测出异常；对比图6(a)和图6(d)可以看出，TSOD方法只能检测出原序列的部分异常，且这部分数据是凸出正常模式的序列点，而将异常模式中与正常模式序列点数值相近的点看作正常数据，由此可以看出TSAD方法和ESAA方法对Aritificial_Data数据的检测效果最好，TSOD方法的检测效果最差。

图5 三种方法对Keogh_Data数据实验结果

图6 三种方法对Aritificial_Data数据实验结果

3.2.2 实验评估

为评价所提出的时间序列异常检测方法的实验结果，采用检测率(Detecton Rate, DR)、误报率(False Positive Rate, FPR)和漏报率(False Negative Rate, FNR)作为算法检测性能的度量指标[16]。检测率是指异常行为被正确检测出来的比率，如果检测算法不能精确地描述正常行为，那么就必然会出现各种误报的情况，如果把正常行为误报为异常行为，此情况称为误报；把这种错误情况所占正常行为的比率，称为误报率。如果有异常行为不能被识别，无法被检测出，这种情况被称为漏报；把漏报的异常行为所占所有异常行为的比率，称为漏报率[17]：

DR=(Y∩Y′)/Y

(9)

FPR=[Y-(Y∩Y′)]/(X-Y)

(10)

FNR=[Y-(Y∩Y′)]/Y

(11)

其中:X代表数据集，Y代表X中的异常数据集，Y′代表算法检测出的异常数据集。

表3中给出了基于频繁模式的时间序列异常检测方法(TSAD)、基于扩展符号聚集近似的水文时间序列异常挖掘方法(ESAA)和基于滑动窗口预测的水文时间序列异常检测方法(TSOD)对MRN_measles、Keogh_Data和Aritificial 三种数据的检测实验结果。

由实验结果可以看出， MRN_measles和Keogh_Data两种数据用TSAD方法的检测效果最好，Aritificial_Data数据用ESAA方法的检测效果最好，用TSAD方法的检测效果也很好，对于这三种不同类型的数据，TSAD方法的平均检测效果是最好的，并且比另外两种方法好很多。同时由表3度量结果中的方差可以看出, TSAD方法的偏好性最小，对三种数据的检测效果都非常好，ESAA方法对数据的偏好性最大，对Aritificial_Data数据的检测率高达0.99，且误报率为0，但对Keogh_Data数据的检测率为0，分析其原因可以看出该算法对序列的噪声非常敏感，会将一些噪声误认为异常, 导致其受噪声干扰性很严重， TSOD方法是三种方法中检测效果最差，对三种数据的检测率都很低，对Aritificial_Data数据的检测相对于另外两种数据较好，对数据的偏好性较严重，该方法也是受噪声干扰大，但相对于ESAA方法较好一点。

表3 三种方法对比实验结果

由结果对三种方法进行分析可看出，本文方法主要考虑的是序列整体的趋势，在符号序列化中平滑了一些噪声的干扰能很好地检测出异常。相对于序列整体的异常，而对比方法TSOD更多考虑的是局部特征，该方法的主要思路是通过序列中任意一点的k近邻点对该点进行预测，如果预测值与该点实际值不超过预设阈值则可判定该点为正常点，反之为异常，该方法更多受到序列局部特征的影响，而且对序列所有元素值没有进行其他提取效果，所以受噪声干扰大；而ESAA太注重最值的影响，因此噪声干扰性更强。总体来说，三种方法中TSAD最好，其次为ESAA，TSOD最差。

3.2.3 时间复杂度分析

在此假设需检测序列的长度为m，TSAD方法截取前n(n

3.2.4 实验总结

比较三种方法对三种不同数据的检测效果和时间复杂度可以看出，TSAD方法的时间复杂度比TSOD方法稍大一点，但检测效果明显好很多，尤其是对于增量式数据，当增加的数据 趋于无穷大时，TSAD方法和TSOD方法的时间复杂度近似相同，但检测效果好很多。总的来说，TSAD方法是最好的。

4 结语

针对传统方法的复杂性和高消耗性，本文提出的基于频繁模式的时间序列异常检测方法能较好改善这一问题，该方法同时从序列整体形态和局部特征的角度研究，能较准确地发现序列中的异常片段，并且该方法使用的是对同种序列的一次性挖掘，在找出一种序列的频繁模式后该序列新增加的数据便不再作频繁模式的挖掘，只需执行简单的相似性度量就可以检测其中的异常片段。 本文方法的优点在于能基于正常数据的频繁模式检测新加入数据的异常，实现动态数据的异常检测，并且对于新加入的数据只需与先挖掘的频繁序列进行简单的比较实验，不用耗费太多资源； 但该方法也存在一些缺点，如参数太多，导致在运行时调整参数太过复杂。进一步的改进方案需对参数进行优化，尽量地减少参数复杂性，同时对符号化表示方法进行优化，使其能更好地表示序列的形态，对频繁模式的挖掘起到更普遍的作用，能够更好地去发现现实生活中的动态数据异常，免受噪声数据的干扰。