基于Workbench的FSAE传动系统的有限元分析

王西洋，徐家川，王橙，王孟恩，焦学健



基于Workbench的FSAE传动系统的有限元分析

王西洋，徐家川，王橙，王孟恩，焦学健

（山东理工大学交通与车辆工程学院，山东 淄博 255000）

FSAE赛车的轻量化设计很大程度上是靠有限元软件实现的，文章在CATIA中对FSAE传动系统建立三维模型，通过理论分析进行受力计算；针对传动系统中的架载荷特性，建立大链轮和偏心轮支架的有限元模型，对其进行模态与静力学分析，得到其安全系数云图，在此基础上，文章对链轮与支架的结构进行优化，使得镂空处的尺寸最合理，保证其在满足强度的要求下，质量最轻。通过对优化后的结构再次分析，结果表明该链轮与偏心轮支架的结构优化设计是可行的。

FSAE传动系统；链轮；结构优化；轻量化

引言

本文运用有限元结构分析的方法，在三维软件CATIA中建立三维模型，并对模型进行计算受力分析；利用ANSYS软件对模型静力学结构强度分析，并进行结构优化。

1 传动系统机械结构

1.1 布置方案

由于赛车采用发动机中置后驱的布置形式，后桥空间紧凑，故赛车采用传动效率高、过载能力强的链传动，传动系机械结构的设计的主要任务包括传动系与车架的安装机构，链条张紧机等[4]。

1.2 传动系统链条张紧机构的设计

车队自成立以来曾用过固定式机构、正反丝链条张紧机构以及垫片调节结构。综合考虑其优缺点，今年采用如图1所示的拆装、调节更为方便的偏心轮链条张紧机构。

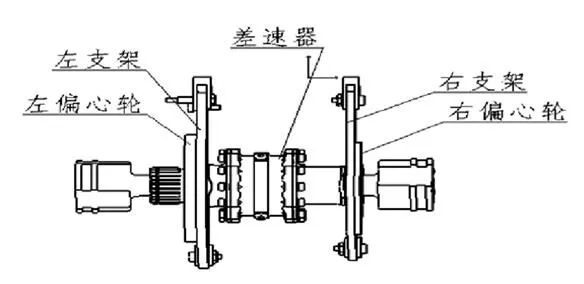
图1 链条张紧机构

1.3 大、小链轮的结构设计

小链轮的齿数1对链传动的平稳性和使用寿命有较大影响，齿数不宜过多，也不宜过少，考虑后桥的空间，根据计算得末级传动比i=3.181，由于链节数通常是偶数，为使链条磨损均匀，常取链轮齿数为奇数，并尽可能与链节数互质[5]，故取小链轮齿数1=11，大链轮齿数为35。通过CATIA对大小链轮进行参数化模型建立，如图2。

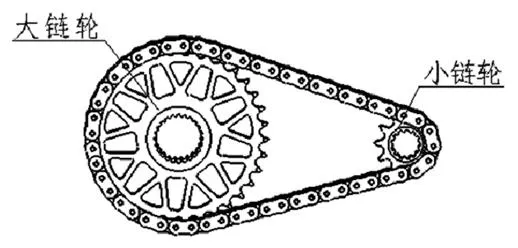
图2 链轮总成

1.4 受力计算

1.4.1 链条张紧机构

本文张紧机构为偏心轮，其外部通过螺栓与支架连接，内部放置轴承，主要承受来自轴承载荷，在分析的时候将偏心轮与支架固接成一个整体，即偏心轮支架。以发动机最大输出扭矩计算，由于车队使用的是本田CBR600F4iRR发动机，其相关参数如表1。

表1 发动机相关参数

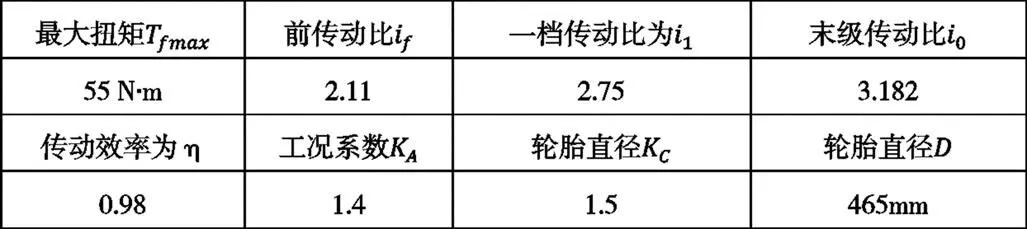
可知链轮受力

至于对停在路边未上锁的车上私锁的行为，笔者认为同样构成侵占罪。理由在于停在路边未上锁的车属于遗忘物，遗忘物与遗失物的区别在于遗忘物是由于财物的所有人、持有人的疏忽，或者遗忘而暂时失去占有、控制的财物。其特点是遗忘的时间短，遗忘物依然处于失主可能控制的范围之内，失主如果及时采取措施，将会很快恢复对该物的控制。在共享单车停在路边未上锁的情况下，共享单车公司还能够通过电子锁对其进行定位，但是由于其未上锁，因此其处于一种不确定的状态之下，可以认为其处于一种被遗忘的状态，但当再关上锁时，就可回复到一种完全的占有状态。

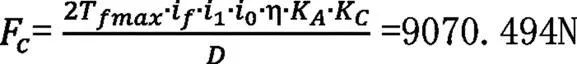
即可算得支架处左右轴承分别承受力：

1=11247.413N

2=2176.919N

故左右偏心轮所承受轴承力大小分别为1、2。

1.4.2 链轮总成

本文主要分析大链轮，其危险工况为发动机在1档时的弹射起步，取其最大扭矩计算，由(1)式计算链轮受最大拉力为F=9070.494N。

2 有限元模型建立

2.1 选择材料及网格划分

2.1.1 材料选择

基于实际需要及轻量化目标，大链轮、偏心轮及支架选择7075-T6铝合金材料，屈服极限σ=462MPa，安全系数取1.5，则许用应力为[]=308 MPa。

2.1.2 网格划分

根据分析对象和目的，确定有限元网格划分方案，建立有限元分析的计算模型。使用Multizone多区域网格化分，实现面体与楔形单元的有效划分，增加网格划分精度，减少出错机会[6]。

将链轮分为接触区和非接触两个部分，采用不同的网格密度及划分方法，其中接触区域的网格最小并进行局部网格划分；对链条张紧机构中的支架进行多区网格划分。

2.2 施加载荷及约束

将大链轮导入ANSYS中，在大链轮链齿的分度圆处施加11个切向力，大小为1000N[7]，并在大链轮花键孔处施加固定约束。在支架上下孔处分别施加圆柱约束，在偏心圆处施加一轴承载荷为F=11247.413N，同理，右偏心轮机构一样。

3 静力学分析

3.1 大链轮、偏心轮支架静力学分析

图3 大链轮安全系数

图4 偏心轮支架安全系数

根据车队以往设计经验以及轻量化的目标，将安全系数定在1.5，通过计算得到大链轮与偏心轮支架的安全系数分别如图3、图4。

根据所取安全系数，由安全系数云图可知大链轮最小安全系数为2.46，偏心轮支架最小安全系数为3.42，基于轻量化的目标，其结构设计过于保守，故对其进行结构优化。

4 结构优化

结构优化的目的在于最大限度的减重，通过改变减重孔的大小并在保证相关要求的情况下使其最轻。

4.1 偏心轮支架优化

由上述静力分析结果可知偏心轮支架的镂空区域还有很大的优化空间，故将支架棱厚、偏心轮镂空圆弧半径定义为变量参数，其响应结果如图5、图6、图7。

图5 总质量随圆弧直径的变化

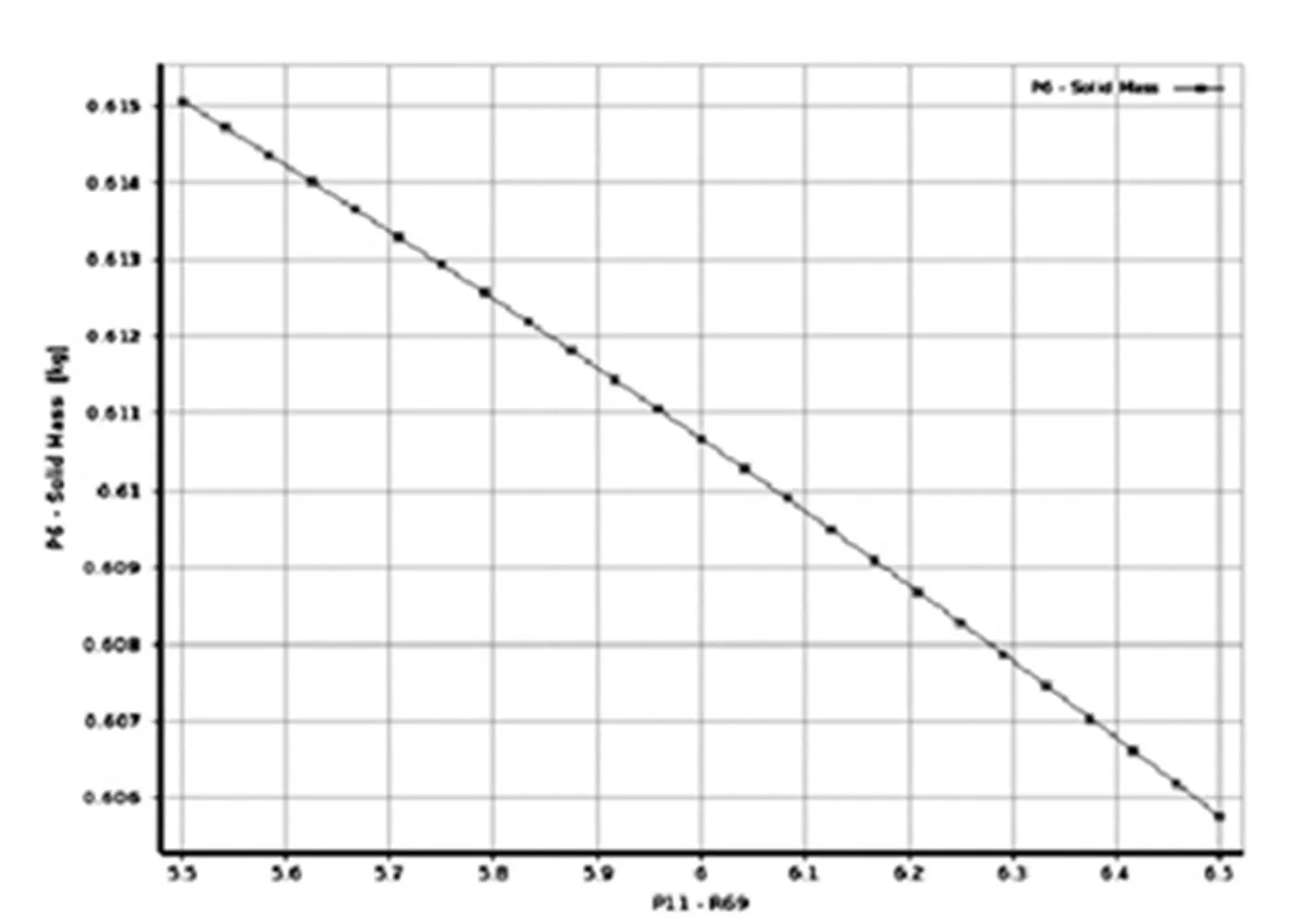
图6 最大应力随圆弧直径的变化

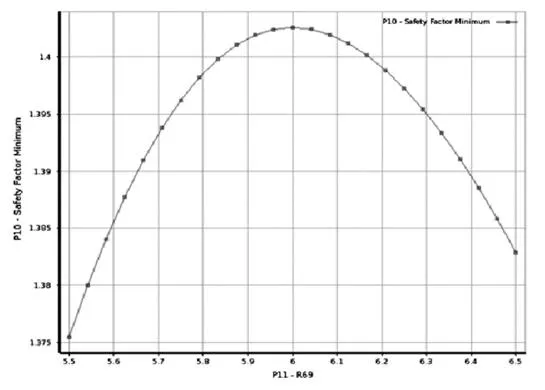
图7 安全系数随圆弧直径的变化

如图5所示，随着圆弧直径的增大，其总质量不断变小；如图6所示，最大应力随着圆弧直径的增大而先减小再增大，在圆弧直径为6mm时，其最大应力最小；如图7所示，安全系数随着圆弧直径的增大而呈现先增后减的趋势，在圆弧直径为6mm是，其安全系数最大。

当产生一个设计后，要对方案进行评估[8]，首先查看更新后的几何模型，然后用优化后的参数重新进行静力学仿真，优化后的仿真结果与优化前的对比如表2。

表2 优化前后数据对比

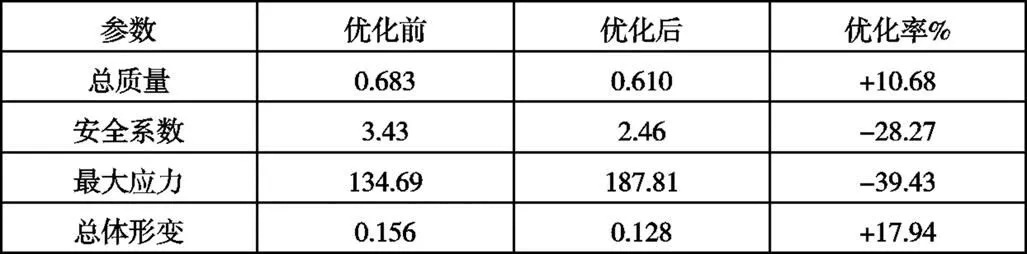
从结果中可以看出，总质量及总体形变优化后相比优化前，其优化率有明显的变化，其安全系数有所下降，但在允许的范围之内，可见此优化方案具有实际意义。

4.2 大链轮优化

通过分析得到的应力应变云图以及安全系数分布并对其进一步分析后，设定优化参数如表3。

表3 优化参数表

优化结果首先看响应图，通过上述参数，得到大链轮质量、安全系数、总的变形随凹槽尺寸的变化如图8、图9、图10。

图9 总质量随凹槽尺寸变化

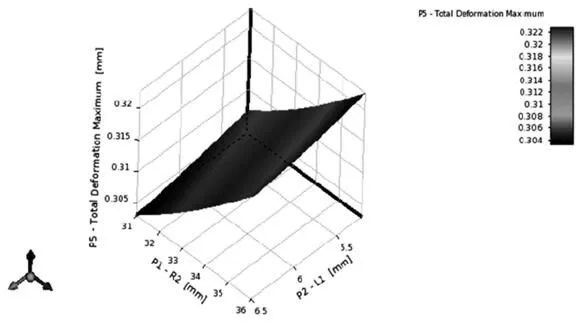
图10 总体形变随凹槽尺寸变化

由以上响应图可知，每一个点对应一个优化的凹槽尺寸，由计算结果可得到如下表4所示的设计点。

表4 优化设计点参数

表5 优化前后数据对比

通过比较表6中三个设计点，在保证大链轮强度要求的前提下，使得大链轮总质量尽可能的小，从安全系数角度考虑，DP2强度最高；从总质量方面考虑，DP3最轻；从总体形变角度考虑，则DP1变形最小。本文从轻量化的角度考虑，故取DP3为最终优化点，将优化前与优化后进行对比如表5。

由表7可知，参数优化后，大链轮的厚度更薄，质量由0.316kg降为0.253kg，降低了%16.90，但同时其最大应力增大，安全系数变小，总体形变也有所增加，但总体上符合大链轮的强度要求。

5 结论

通过对偏心轮支架与大链轮进行参数设置，通过计算得到其优化点，将优化点参数导进原有模型重新进行静力学仿真，偏心轮支架质量由0.683kg降到0.610kg，大链轮质量有0.316kg降到0.253kg，可见此设计方案对赛车的轻量化设计具有一定的意义。

参考文献

[1] 邵鹏礼,魏来生,贾爽.传动箱有限元强度计算与优化[J].车辆与动力技术,20022(3):31-35.

[2] 刘波,郑忠才.7YPJ.型农用三轮汽车齿轮箱体有限元静力分析[J]山东建筑大学学报,2007,122(5):434-437.

[3] 刘春美,李梦群,丁爱玲.汽车变速箱箱体的动态设计[J]山西机械, 2000（增刊）:8-9.

[4] 魏琛琛,刘浩凌等.FSAE 方程式赛车传动系统的优化设计及LSD的调教[J].汽车实用技术.2017.

[5] 高伟,邓召文,严子雄.FSC赛车链传动系统的设计与分析[J].汽车实用技术2014.

[6] 王明强,朱永梅,刘文欣.有限元网格划分方法应用研究[J].机械设计与制造,2004,2(1):22-24.

[7] 王嬿舒,基于ANSYS的方程式赛车传动系统优化设计[J].机械传动,2017.

[8] 袁素粉,袁晓红,陈昌生.基于ANSYS Workbench的半挂车车轴的强度分析及其优[J].北京汽车,2011.

Finite element analysis of FSAE drive system based on Workbench

Wang Xiyang, Xu Jiachuan, Wang Cheng, Wang Mengen, Jiao Xuejian

( School of transportation and vehicle engineering, Shandong university of technology, Shandong Zibo 255000 )

Abstract: The lightweight design of FSAE car is largely realized by finite element software. In this paper, a threedimensional model of FSAE transmission system is built in CATIA, and the force is calculated through theoretical analysis. For the load characteristics of the frame in the transmission system, the finite element model of the large chain wheel and eccentric wheel support is established, and its modal and static analysis is carried out to obtain the safety factor cloud map. On this basis, this paper optimizes the structure of sprocket and bracket, so as to make the dimension of the hollow-out most reasonable and ensure the lightest quality under the requirement of strength. The results show that the optimal design of sprocket and eccentric support is feasible.

Keywords: FSAE car transmission; Sprocket; Structure optimization; Lightweight

CLC NO.: U463.2

Document Code: A

Article ID: 1671-7988(2018)21-53-04

中图分类号：U463.2

文献标识码：A

文章编号：1671-7988(2018)21-53-04

作者简介：王西洋，男（1997-），男，就读于山东理工大学交通与车辆工程学院，本科三年级。徐家川，男，山东理工大学副教授，主要从事汽车车身设计、车身曲面光顺、尺寸控制等方面的教学与研究工作。

10.16638/j.cnki.1671-7988.2018.21.019