基于HMM的锂电池仓火灾预测算法研究*
张绪祥,高扬
基于HMM的锂电池仓火灾预测算法研究*
张绪祥,高扬
(长安大学 汽车学院,陕西 西安 710000)
针对电动车锂电池仓环境监测困难以及引起火灾因素复杂导致预测火灾不准确的问题,提出一种基于隐马尔可夫模型的火灾预测方法。该方法将锂电池仓的温度场特征作为隐马尔可夫模型的观测变量,运用极大似然估计法建立用于预测火灾状态的隐马尔可夫模型。实验结果表明该方法在解决锂电池仓火灾预测的问题上具有较高的准确性。
锂电池仓;火灾预测;隐马尔可夫模型
前言
电动汽车作为汽车产业的主要发展方向之一,其使用价值在人类生活中发挥的作用将越来越重要,随之而来的电池安全问题也越来越受到人们的关注,由于车辆锂电池仓环境复杂,难以实施有效监控,容易引发火灾事故,若发生火灾或引发爆炸,势必将造成巨大财产损失,造成较大的社会影响。因此,研制一个能在火灾发生初期,对车辆安全没有造成严重伤害时,就能够及时的发现火情的智能监控系统对车辆安全来说是十分重要的。
目前国内已有大量研究针对公共交通的防火问题,大多数是应用于大型建筑、船舱以及飞机舱内部的环境监控与火灾预测[1-3],并未对锂电池仓这一特殊环境的火灾预测问题进行有针对性的研究。
在研究方法上,目前的火灾预测方法主要基于对环境信息的监测[4],当监测到环境特征异常时即刻进行报警。主要方法包括:多传感器数据融合法、图像识别法、神经网络法。如傅剑锋等采用数据融合的三层结构,对明火的特征识别[5];杨娜娟等提出一种基于向量机的图像型火灾预测放法,避免了所需样本较多带来的实验和计算复杂的问题[6];杨帮华等建立了串联型神经网络,将神经网络运用到火灾识别中[7]。此类研究有效地提高火灾预测的准确性,但数据融合法和神经网络法在一定程度依赖大量的数据集,图像法成本较高,实时性较差,同时,由于锂电池在工作过程中自身会产生热量,此类方法在区分明火和热源的研究上还存在不足。
本文将隐马尔可夫模型(Hidden Markov Model,HMM)应用于锂电池仓火灾预测的研究中。HMM作为一种统计分析模型,创立于20世纪70年代,被广泛应用于语音识别、机械故障诊断等领域[8]。在火灾预测中最关键的是HMM参数的估计的问题,其中观测状态转移概率矩阵描述了观测变量与状态变量之间的概率关系。本文就锂电池火灾预测问题提出一种HMM参数的训练方法,实验结果证明,该方法能较大的提高火灾预测的准确性。
1 基于隐马尔可夫模型的火灾预测
1.1 隐马尔可夫模型简介
HMM属于双随机过程,它既能反映对象的随机性,又能反映对象的潜在联系,用来描述一个含有隐含未知参数的马尔可夫过程。HMM的参数用λ={,,,,}表示。它用来解决三个基本问题:
(1)概率计算问题,已知模型参数,计算出现当前观测序列的最大概率,其公式为:
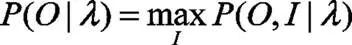
(2)最优问题,已知模型参数,寻找出现当前的观测序列的状态序列,其公式为:

(3)参数估计问题,已知观测序列,估计模型参数,其公式为:
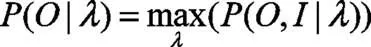
1.2 基于HMM的火灾预测
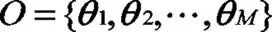
1.2.1 观测变量分析
由于锂电池仓是一个相对封闭的环境,无法直接观察到仓内的情况,因此需要通过采集仓内的温度、烟雾等信息来判断。就火灾的发展过程而言,火灾发生初期的温度场特征为各点温度分布不均匀,为了能准确的识别火灾,本文对火灾发生初期的温度场特征进行分析,但由于温度场特征计算过于复杂,本文提出了一种由参数来描述温度场特征的方法。
本文按同等比例创建了锂电池的空间几何简化模型,模拟锂电池仓的火灾发生的情况。根据锂电池仓的大小,分别设置了了明火(如图1)和热源(如图1)来模拟火灾和锂电池工作发热。

图1 火灾模拟



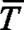
将式中的两个参数归一化得到参数的表达式:
由于明火和热源这两种温度特征和两个温差系数不是一一对应的关系,具有一定的不确定性,参数可以描述某温度场特征是明火温度场特征的程度。当为1时,该温度场最大程度上为明火温度场,当为0时,该温度场最大程度上为热源温度场。
1.2.2 火灾预测模型训练
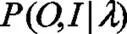



其中,(1=)表示在初始时刻状态变量为的数量,C表示从状态转移到状态的数量,C表当状态为时,观测状态为的数量。
针对锂电池仓明火和热源两种场景的识别进行隐马尔可夫模型的训练,由于明火和热源火这两种状态变量互相转移的概率较小,因此初始状态概率矩阵和状态转移概率a的初始设置对识别正确率的影响不是很大,状态变量对应的观测变量的概率b的相对于其他两组参数来说对结果的准确率来说更重要,因此本文主要针对参数进行训练。将温度值计算得到值,对这些值进行分类,识别它们属于明火状态还是热源状态,实质上就是对温度场的特征值进行分类[9]。具体的训练过程如下所示:
根据锂电池仓大小本文选择6个温度传感器采集仓内温度数据作为一组温度值,分别选出100组明火场景下采集的温度数据和100组热源场景下采集的温度数据对模型的参数进行训练。其中每组温度数据均转化为值用以描述温度场特征,计算得到200组值作为观测变量统计得到在明火和热源状态下温度场特征值的分布情况,如图2所示:

图2 θ值的分布
由图2得知:明火状态和热源状态的值的分布区别很大,在明火的状态下,值的分布情况如表1:
表1 着火状态θ值的分布

根据统计的结果,当温度度处于明火状态时,有97%的值处于0.6和0.65之间,在热源状态下值均为0。
依据上述统计结果可得到隐马尔可夫模型的参数,对于变量,存在2种状态:明火状态和热源状态;对于观测状态,存在2种值的分布情况:
处于0.6至0.65之间或者为0。即隐马尔可夫参数可设置为:

式中矩阵的行向量表示明火与热源2种状态,矩阵的列向量表示值的2中分布区间。
那么对于明火的和热源这两种状态来说,在这两种状态之间的转变时锂电池仓内的温度变化是一个持续的过程,所采集到的温度在短时间内都将维持它们原有状态的值,从两种状态的开始发生转移开始到转移完成,中间所包含的属于前一状态的温度特征值的组数在整个转移过程中所有的特征值的组数中所占的比率既为两种状态的自转移概率,根据是历史数据可将隐马尔可夫模型的参数可设置为:

式中矩阵的行向量和列向量都表示明火和热源这2种状态。
初始隐性状态概率的值本文采用均值法,因此隐马尔可夫模型的参数可设置为:
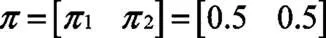
式中矩阵的列向量表示明火和热源2种状态。
1.2.3 火灾预测
对于火灾预测问题,在得到隐马尔可夫模型的参数之后,利用维特比算法来计算在某一时刻的状态变量的概率,而概率最大的状态变量即认为当前时刻所处的状态。
维特比算法首先运用递推的方法求得在给定的模型参数的条件下,得到的观测序列为=(1,2,…,θ)的概率,与之不同的是维特比算法需要记录每一次递推之后产生最大概率的状态变量,并在递推结束后输出这些状态变量序列[10]。总的来说,维特比算法的求解过程可描述为:输入任意状态下的温度场特征值1,2,…,θ,输出每个温度特征值所隐含的着状态是明火或者热源,具体计算公式如下:
定义变量δ()表示在给定的模型参数的条件下,在时刻锂电池仓里的状态为,且温度场特征值在某一个区间的最大概率,ψ()记录了在-1时刻的状态变量,该状态在时刻转移到其他状态并使得此时值在某一区间的概率最大。具体过程描述如下:
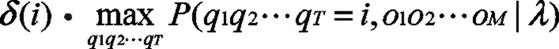

初始化上述变量得到在初始时刻出现某温度场特征值的最大概率,由于在初始时刻的前一时刻不存在任何状态,因此此时记录的状态为0,具体公式为:
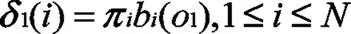
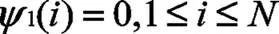
同初始化过程相同,依次计算不同时刻的最大概率值并记录相应的状态变量:

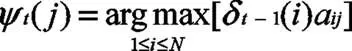
计算至最后时刻终止:
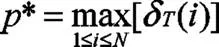
至此,对整个马尔可夫链进行了递推计算,并且每一次递推求得的概率都是最大的,接下来通过状态变量序列回溯路径得到所有的状态变量序列:

2 实验验证
2.1 传感器采集系统的设计
传感器信息采集采用模块化设计[11],温度采集模块选用智能巡回检测仪,它集成了包括温度传感器和AD转换模块,并且提供了RS232串口用于向中央控制器传输采集到的信息,串口通讯模块的型号为MXA3232[11],为了方便处理实验数据和实时观察数据,加入了SD卡采集模块和液晶屏显示模块。中央处理器选用STM32F103开发板,该开发板上的UART接口用于中央处理模块与执行模块之前的通信,并能够及时处理传入的温度信息。实验如图3所示:

图3 实验硬件
2.2 检验隐马尔可夫模型火灾预测的准确性
在得到符合该模型的隐马尔可夫参数之后,利用该模型对锂电池的火灾情况进行预测。在这里本文同样使用大小和锂电池仓相近的试验箱模拟明火和热源场景。选取100组明火实验的数据和100组热源实验的数据,利用Python编程实现对着200组数据的识别判断,同时针对锂电池仓温度多变的情况设计了冷热环境实验,将温度传感器分别放置在2~8摄氏度的冷室和60~70摄氏度的热室并交换放置多次,同样选择100组数据利用该模型进行识别判断,此时判断为不着火为判断正确,这三种实验环境数据的识别结果如表2所示:
表2 预测结果
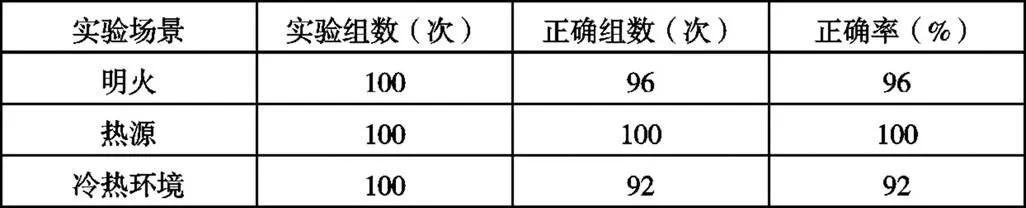
其中,在100组明火实验的数据中,能正确识别的组数为96组,正确率为96%,在100组热源实验的数据中,能正确识别100组,正确率为100%,在100组冷热环境实验的数据中,能正确识别92组,正确率为92%。
除了以上所做的模拟锂电池仓环境实验,本文还进行了实车环境实验,使用实车采集到的环境温度数据进行识别。各传感器在锂电池仓的安装位置如图4所示。将采集一天的数据进行识别判断,由于在实验阶段实车并没有发生着火,因此判断为不着火为正确判断。

图4 实车安装
将采集一天的数据进行识别判断,由于在实验阶段实车并没有发生着火,因此判断热源为正确判断。将正确的判断记为1,错误的判断记为0,实验结果如图5所示。

图5 实车测试结果
在这一天的测试中,将近46400组数据,其中也仅仅有200组数据识别错误,这些错误的数据相对比较集中。由模拟实验和实车实验可以看出,模拟实验制造了一种恶劣的的温度易突变的环境,在这种情况下判断的正确率较低,而在实车实验中的温度稳定的情况下,判断的正确率较高。
3 总结
根据锂电池仓内着火前期仓内温度场特征,提出了一种用参数描述温度场特征的计算方法,利用隐马尔可夫模型具有双重随机这一特质,找出了锂电池仓内明火这一状态和仓内温度场的特征存在着概率关系,研究建立了基于温度场特征的火灾预测方法,有效的预测出隐含在温度信息下的状态信息,并依托隐马尔可夫模型的学习训练能力对历史数据进行整理归纳,使得预测的结果更准确。
[1] 沈雄,林榕.高层建筑的智能防火系统[J].上海海运学院学报,2001 (02):21-23+28.
[2] 王燕,顾冬华,姚瑶.贝叶斯网络在舰船安全性评估模型中的应用[J].舰船科学技术,2016,38(18):157-159.
[3] 景宏令,陈龙,匡勇.飞机发动机舱灭火剂用量试验验证与优化研究[J].火灾科学,2016,25(04):204-207.
[4] 陈涛,翁文国,孙占辉,苏国锋,袁宏永.基于火灾模型的消防应急平台架构和功能分析[J].清华大学学报(自然科学版),2007(06):863- 866.
[5] 傅剑锋,雍静.基于数据融合技术的火灾探测算法[J].低压电器, 2007(12):22-24+48.
[6] 杨娜娟,王慧琴,马宗方.基于支持向量机的图像型火灾探测算法[J].计算机应用,2010,30(04):1129-1131+1140.
[7] 杨帮华,董峥,张永怀.模糊神经网络在火灾探测中的应用[J].自动化仪表,2011,32(10):48-51.
[8] Yuan Lichi. Improved hidden Markov model for speech recognition and POS tagging[J].Journal of Central South University,2012,19 (02):511-516.
[9] 张明卫,朱志良,刘莹,张斌.一种大数据环境中分布式辅助关联分类算法[J].软件学报,2015,26(11):2795-2810.
[10] 徐超颖,杨国安,石永光,郑南宁.卷积码及其维特比译码算法的软件实现[J].西安交通大学学报,2003(02):151-154.
[11] 张燕波,沈广平,董自强,秦明,黄庆安.基于微控制器的风速风向传感器系统设计[J].仪器仪表学报,2009,30(10):2144-2149.
Research on Fire Prediction algorithm of Lithium Battery Warehouse based on HMM*
Zhang Xuxiang, Gao Yang
( School of Automobile, Chang'an University, Shaanxi Xi'an 710000)
Aiming at the difficulty of environmental monitoring of lithium-battery storage in electric vehicles and the inaccuracy of fire prediction caused by complex fire factors, a fire prediction method based on hidden Markov model is proposed. In this method, the temperature field of the lithium battery bunker is taken as the observed variable of the hidden Markov model, and the hidden Markov model for predicting the fire state is established by using the maximum likelihood estimation method. The experimental results show that the method is accurate in solving the fire prediction of lithium battery bunker.
Lithium battery bunker;fire prediction;hidden Markov model
U469.72
B
1671-7988(2018)21-05-05
U469.72
B
1671-7988(2018)21-05-05
张绪祥,长安大学硕士研究生。
国家自然科学基金 61503043,陕西省自然科学基金项目2015JQ6214中央高校基金(310822172204),Shaanxi Natural Science Foundation (2017JM7016)。
10.16638/j.cnki.1671-7988.2018.21.003

