聚焦三视图的题型
■徐春生
空间几何体的三视图是新课标教材中增加的内容,是观察者从不同位置观察同一个空间几何体画出的图形,它从细节上刻画了空间几何体的结构。涉及的试题一般以选择题形式出现,考查同学们的空间想象能力及运算与推理能力。常考题型有根据几何体的直观图画三视图,根据几何体的三视图画直观图,根据三视图求原几何体的面积和体积,根据三视图研究原几何体的性质等。下面分别举例分析,希望对大家的学习能有所帮助。
一、根据几何体的直观图画三视图
例1 用一个平行于水平面的平面去截一个球,得到如图1所示的几何体,则它的俯视图是( )。
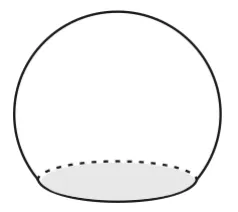
图1

由题意知,俯视图中显然应有一个被遮挡的圆,所以内圆是虚线,故选B。
在画三视图时,可见的线要画为实线,不可见的线要画为虚线。三视图摆放规则:上面是正视图和侧视图,正视图下方是俯视图,正视图、俯视图“长对正”,正视图、侧视图“高平齐”,俯视图、侧视图“宽相等”。
例2 一个几何体的正视图和俯视图如图2所示,则相应的侧视图可以为( )。

图2
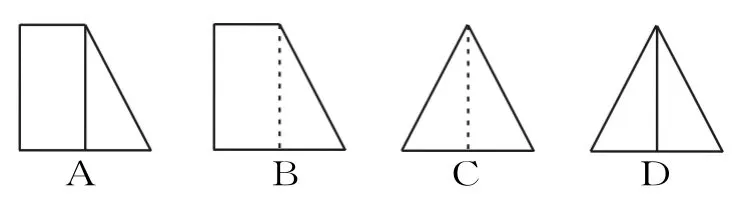
由几何体的正视图和俯视图可知,该几何体应为半圆锥和一个有一侧面(与半圆锥的轴截面为同一个三角形)垂直于底面的三棱锥的组合体,故其侧视图应为D。
空间几何体的三视图是该几何体在三个两两垂直的平面上的正投影,并不是从三个方向看到的该几何体的侧面表示的图形。
二、根据几何体的三视图画直观图
例3 如图3,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )。

图3
A.三棱锥 B.三棱柱
C.四棱锥 D.四棱柱
由题意知,该几何体的三视图为一个等腰直角三角形和两个长方形,经分析可知该几何体为三棱柱,故选B。
解决此类问题的关键是能根据几何体的三视图判断出几何体的结构特征:①三视图为三个三角形,对应的几何体是三棱锥;②三视图为两个三角形和一个四边形,对应的几何体是四棱锥;③三视图为两个三角形和一个圆,对应的几何体是圆锥;④三视图为一个三角形和两个四边形,对应的几何体是三棱柱;⑤三视图为三个四边形,对应的几何体是四棱柱;⑥三视图为两个四边形和一个圆,对应的几何体是圆柱。
三、根据三视图求原几何体的面积和体积
例4 某多面体的三视图如图4所示,其中正视图和侧视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形。该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )。
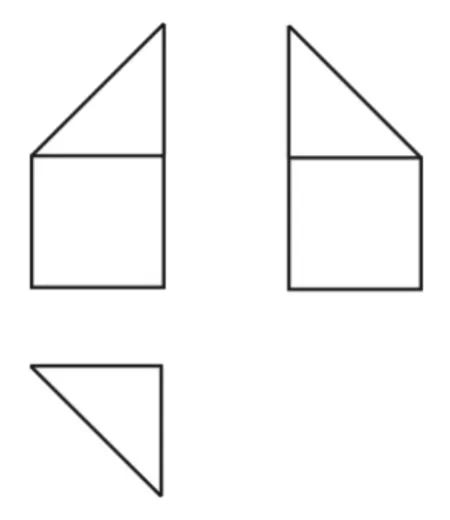
图4

图5
观察三视图可知,该多面体是由直三棱柱和三棱锥组合而成的。直三棱柱的底面是直角边长为2的等腰直角三角形,侧棱长为2,三棱锥的底面是直角边长为2的等腰直角三角形,高为2,如图5所示。因此该多面体各个面中有两个全等梯形,梯形的上底长为2,下底长为4,高为2,所以这些梯形的面积之和为12。故选B。
解答此类问题,一般是先根据给出的三视图判断出该几何体的形状,再确定该几何体的各个度量,最后套用相应的面积公式求解。
例5 如图6,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则此几何体的体积为( )。
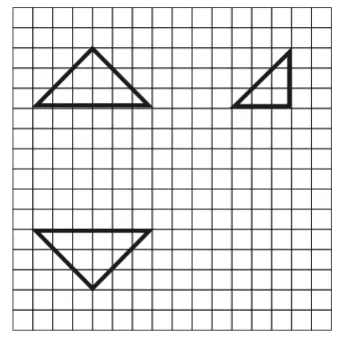
图6
由三视图可知,该几何体为三棱锥,其底面是斜边长为6的等腰直角三角形,高为3,则其体积为6×3×3=9。故选B。
若给定的几何体是柱体、锥体、台体或球体等规则几何体,则可直接利用公式进行求解;若给定的几何体是不规则几何体,则应先将不规则几何体通过分割或补形转化为规则几何体,再利用公式求解;若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解。
四、根据三视图研究原几何体的性质
例6 如图7,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中最长的棱的长度为( )。
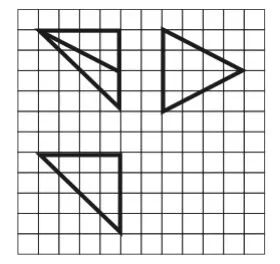
图7
如图8,设辅助正方体的棱长为4,三视图对应的多面体为三棱锥A-BCD,最长的棱为AD。由题意可得,故选C。
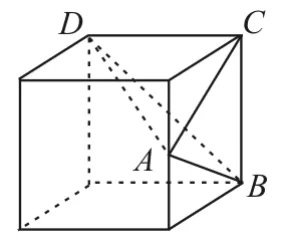
图8
三视图和直观图是空间几何体两种不同的表现形式,通过它们能够从不同侧面、不同角度认识几何体的结构特征,进而研究几何体的有关性质。

