两角差的余弦公式的教学设计

（甘肃省张掖市第二中学 甘肃张掖 734000）

一、教学目标设计

1.知识与技能

通过用向量的方法建立两角差的余弦公式。通过简单运用，使学生初步理解公式的结构及其功能，为建立其他和（差）公式打好基础。

2.过程与方法

通过对学生阅读指导，在公式的探索过程和适当引导，中让学生深刻理解相关概念，领会数形结合的数学思想方法，体会数学知识的形成。

3.情感态度与价值观

经历用向量数量积推导出两角差的余弦公式的过程，培养学生的探索精神，通过分析两角差的余弦公式的结构特征，培养学生的审美能力和学习数学的兴趣。

a、从教材安排来看，前面内容学生已经掌握了一些基本概念，比如三角函数的定义，正弦线，余弦线，两向量的夹角等，为本节学习做了良好的铺垫。

b、舟曲一中是甘南民族地区舟曲县唯一的一所独立高中，学生整体素质比较差，学校主要以艺术特长见长。学生的数学基础相对薄弱，理解能力较差，但是学生思维比较活跃，能积极主动的配合老师学习。大部分学生的思维正从形象思维向抽象思维转化。

c、基于这些实际状况，为突出学生的主体地位，本节课主要采用“阅读和问题引导，启发诱导”的教学方法。整个过程采用问题引导，阅读指导，例题讲解，不断练习方式，让每位学生都参与其中，真正实现使每个学生都得到发展的目标。

二、教学重难点分析

重点：两角差的余弦公式的结构及其运用

难点：通过探索得到两角差的余弦公式

三、教学过程设计

1.创设情景 激发求知

实际问题情境：测算电视塔高度问题（在预习提纲中进行）。

（阅读课本第124页上方引例，并在课前解决问题）

2.自主探究 合作学习

下面一起探讨如何用角∂，β的正弦，余弦来表示cos（ ∂-β）

1.阅读指导：请同学们阅读教材：P125页到P126页：同时思考这样的几个问题：

①我们应该用怎样的思路和方法进行探究？

②教科书上介绍了几种证明方法，各有什么优缺点？

③两角差的余弦公式是什么？

2.解决问题：

问题①：探究分为两个步骤，一是看书 ；二是小组讨论 .

问题②：方法一：利用单位圆中的三角函数线来探究。

方法二：利用向量的数量积、坐标运算来探究。

3.信息交流 揭示规律

对任意的角∂、β，都有sinβ注意：1）公式中的 ∂，β为任意实数。2）两角差的余弦公式特点：公式的左边是 两角差的余弦，右边是 这两个单角的余弦、正弦同名三角函数的积的和。3）学会公式的顺用和逆用。

4. 运用公式 例题讲解

例1、利用差角余弦公式求cos15°的值。

例2.求值：cos175°cos55°＋sin175°sin55°

5. 练习感悟 课堂检测 P127 1，2，3，4

（1）求值与化简

① cos101°cos11°+ sin101°sin11°

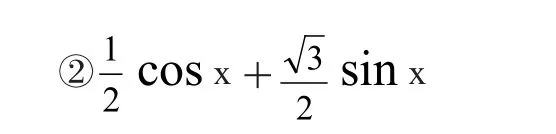
③cos15°cos（x+15°）+sin15°sin（x+15°）

（学生上板练习，教师巡回指导。在民族地区面对藏族学生，基本的练习题目大多数学生还是完成不了，老师在个体辅导后还需重点讲解）

6. 归纳小结 知识概括

①通过本节课学习了哪些知识？

②通过本节课你最大的体验是什么？

③通过本节课的学习你掌握了哪些数学方法？

7.布置作业 巩固提高

作业： P137 A 1、2、3

四、板书设计

五、教学反思

①这是笔者在甘肃省甘南藏州自治州舟曲一中支教时所采用的一份教学设计。

②由于上一章《平面向量》结束匆忙，复习课、小结课，试卷讲评课都安排的相对较少，客观上影响了本节课的学习。

③甘南藏族地区的学生正常的学习习惯还没有养成，看书、思考、探究、小组讨论等活动课内虽有设计，但由于藏族学生基础整体较差，使得许多内容和教学环节不能有效开展。因此，甘南藏族地区的高中数学教学责任重大形势严峻任重道远。