基于Lasso含缺失数据的高斯图模型的模型选择

陈婷 长春工业大学数学与统计学院

一、引言

高斯图模型是一种基于高斯分布假设的无向循环图，也被称为协方差模型选择。Meinshausen and Bühlmann[1]使用Lasso的方法对高维稀疏图进行协方差选择。Yuan[2]将多元线性回归和协方差逆阵中的元素联系在一起，通过线性规划的方式有效地求解高维协方差逆阵的估计。Dempster[3]提出了EM算法，Jiang[4]等提出了E-MS算法，并证明了其收敛性和相合性。

本文主要给出了含有缺失数据的情况下基于E-MS算法的高斯图模型选择的具体步骤即相应的理论推导。第二部分为符号说明；第三部分为理论推导；第四部分为模拟实验；第五部分为结果分析。

二、符号说明

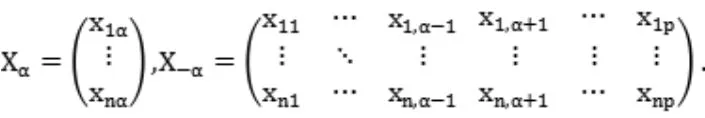
则领域选择问题就转化为求如下的Lasso回归模型：

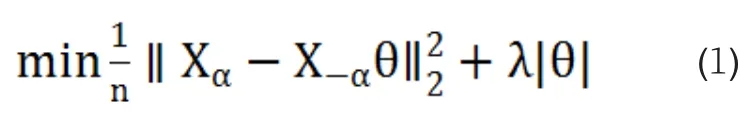
三、理论推导

E-MS的领域选择算法原理：

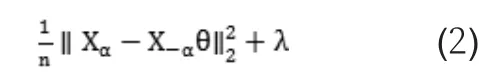
为了把上式最小化，采用坐标轴下降法。

当含有缺失数据时，采用E-MS算法，需要进行E步和MS步，在E步中，给出单调下降序列，然后利用BIC准则选最优的。

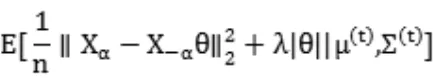
MS步要进行模型选择最小化上式，用坐标轴下降法，易知期望中包含的项为：

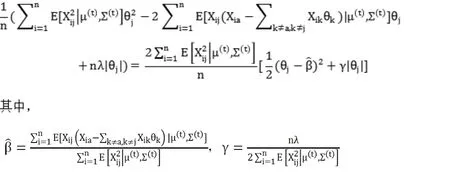
算法步骤如下：

输入：观测数据矩阵X

1.观测样本的分布，按一定的缺失率进行随机缺失；

3.进行如下循环，直至收敛；

4.利用坐标轴下降法得到 的领域，根据完全数据阵Ex求一个图结构G；

5.利用IPS算法求出图结构的极大似然估计。

四、模拟实验

p表示顶点个数，表示样本容量，prec表示正确发现率，mcc表示马修斯系数,tpr表示特效度，tnr表示灵敏度，acc表示真值。在不同样本下进行分析，运用R软件，使用的软件包是：mvtnorm包、MASS包、Matrix包。

表4 .1 缺失率在10%时进行模拟的结果

五、结果分析

在表4.1中可以看出，当p=10时，随着n的个数的增大，prec的值在增大，说明正确发现率在提高，即估计出协方差中正确划分有边的个数与正确划分边的个数的比值在提升；tpr的值有所增大，即估计出的协方差中正确划分有边的个数同正确划分有边的个数与错误划分无边的个数的和的比值在提升；tnr的值有所增大，说明灵敏度在提高，即估计出的协方差中正确划分无边的个数同正确划分无边的个数与错误划分无边的个数的和的比值在提升；acc的值在增大，说明估计出的协方差中正确边的个数也在逐渐变多。当p=15时，随着n的个数的增大，prec、tpr、acc的值同p=10的情况一样，但灵敏度的值在减小，这是在今后的研究中需要改进的地方。